R 中的指数回归(逐步)
指数回归是一种回归类型,可用于对以下情况进行建模:
1. 指数增长:增长开始缓慢,然后迅速加速,无限制。
2. 指数衰减:衰减开始很快,然后减慢,越来越接近零。

指数回归模型的方程采用以下形式:
y = abx
金子:
- y:响应变量
- x:预测变量
- a、b:描述x和y之间关系的回归系数
以下分步示例展示了如何在 R 中执行指数回归。
第 1 步:创建数据
首先,我们为两个变量创建假数据: x和y :
x=1:20 y=c(1, 3, 5, 7, 9, 12, 15, 19, 23, 28, 33, 38, 44, 50, 56, 64, 73, 84, 97, 113)
第 2 步:可视化数据
接下来,让我们创建一个快速散点图来可视化x和y之间的关系:
plot(x, y)
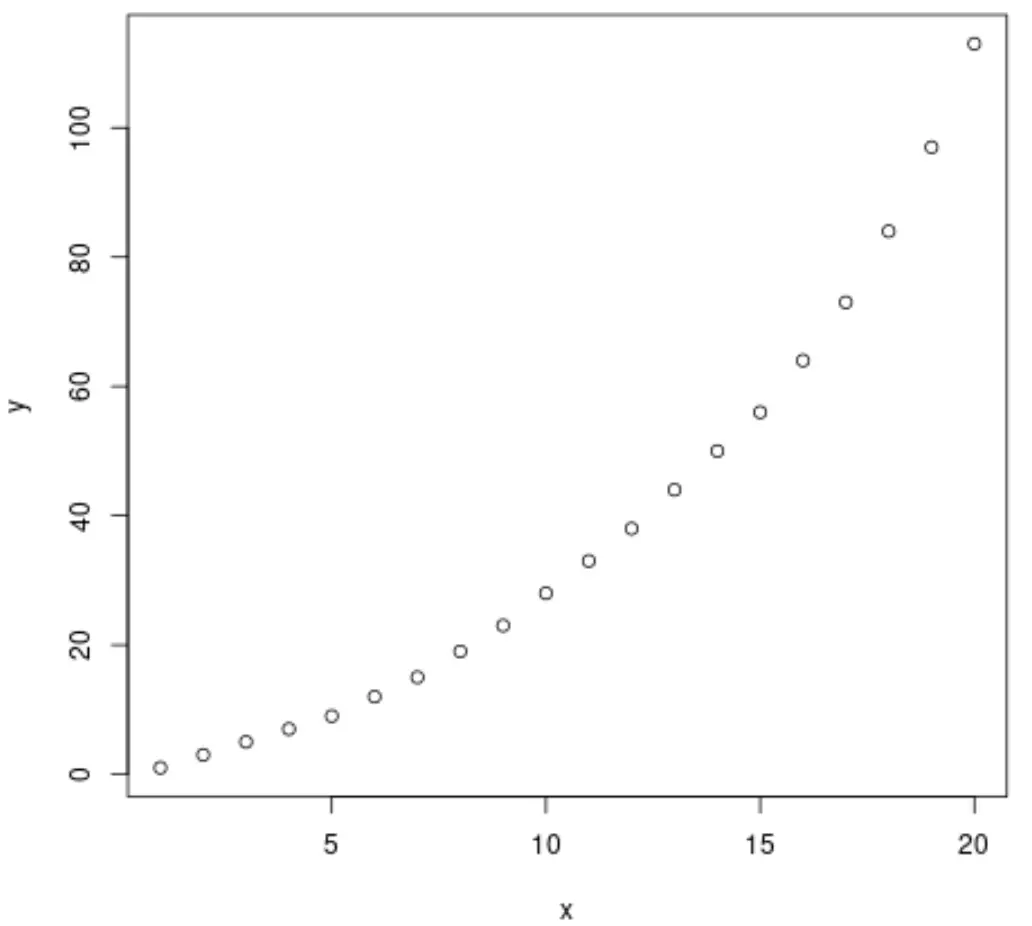
从图中我们可以看到两个变量之间存在明显的指数增长模式。
因此,拟合指数回归方程来描述变量之间的关系似乎是明智的。
步骤 3:拟合指数回归模型
接下来,我们将使用lm()函数拟合指数回归模型,使用y的自然对数作为响应变量, x作为预测变量:
#fit the model model <- lm( log (y) ~ x) #view the output of the model summary(model) Call: lm(formula = log(y) ~ x) Residuals: Min 1Q Median 3Q Max -1.1858 -0.1768 0.1104 0.2720 0.3300 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.98166 0.17118 5.735 1.95e-05 *** x 0.20410 0.01429 14.283 2.92e-11 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.3685 on 18 degrees of freedom Multiple R-squared: 0.9189, Adjusted R-squared: 0.9144 F-statistic: 204 on 1 and 18 DF, p-value: 2.917e-11
模型的整体 F 值为204,相应的 p 值极低(2.917e-11),表明模型整体上是有用的。
使用输出表中的系数,我们可以看到拟合的指数回归方程为:
ln(y) = 0.9817 + 0.2041(x)
将e应用于两边,我们可以将方程重写如下:
y = 2.6689 * 1.2264x
我们可以使用该方程根据预测变量x的值来预测响应变量y 。例如,如果x = 12,那么我们预测y将为30.897 :
y = 2.6689 * 1.2264 12 = 30.897
奖励:随意使用此在线指数回归计算器来自动计算给定预测变量和响应变量的指数回归方程。