R 与 r-square：有什么区别？

学生在统计学中经常混淆的两个术语是R和R 平方，通常写作^R2 。

在简单线性回归的背景下：

• A：预测变量 x 和响应变量 y 之间的相关性。
• R ² ：响应变量中可由回归模型中的预测变量解释的方差比例。

在多元线性回归的背景下：

• A：响应变量的观测值与模型做出的响应变量的预测值之间的相关性。
• R ² ：可由回归模型的预测变量解释的响应变量方差的比例。

请注意，R ²的值介于 0 和 1 之间。该值越接近 1，预测变量与响应变量之间的关系越强。

以下示例展示了如何解释简单线性回归和多元线性回归模型中的 R 和 R 平方值。

示例 1：简单线性回归

假设我们有以下数据集，显示 12 名学生在某门数学课程中的学习时间和考试成绩：

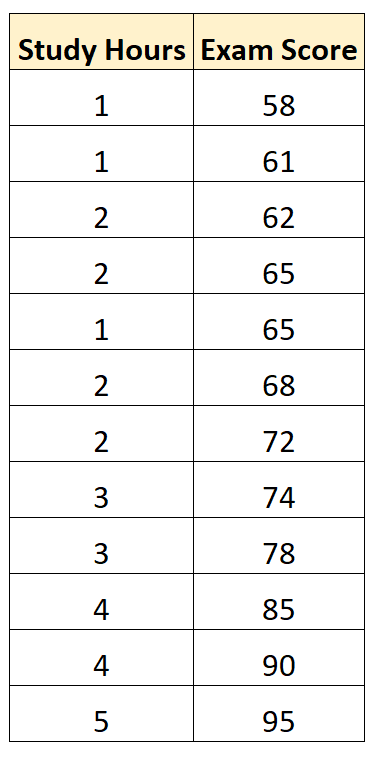
使用统计软件（如Excel、R、Python、SPSS等），我们可以拟合一个简单的线性回归模型，使用“学习时间”作为预测变量，“考试成绩”作为响应变量。

我们可以找到该模型的以下输出：

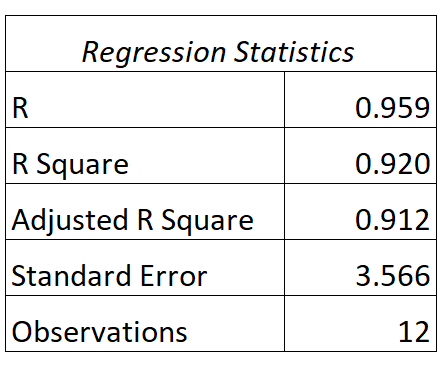
以下是如何解释该模型的 R 和 R 平方值：

• 答：学习时间和考试成绩之间的相关性是0.959 。
• R ² ：该回归模型的 R 平方为0.920 。这告诉我们，92.0% 的考试成绩差异可以用学习时数来解释。

另请注意，R ²值仅等于 R 值的平方：

^R2 = R * R = 0.959 * 0.959 = 0.920

示例 2：多元线性回归

假设我们有以下数据集，显示 12 名学生在某门数学课程中的学习时间、当前学生成绩和考试成绩：

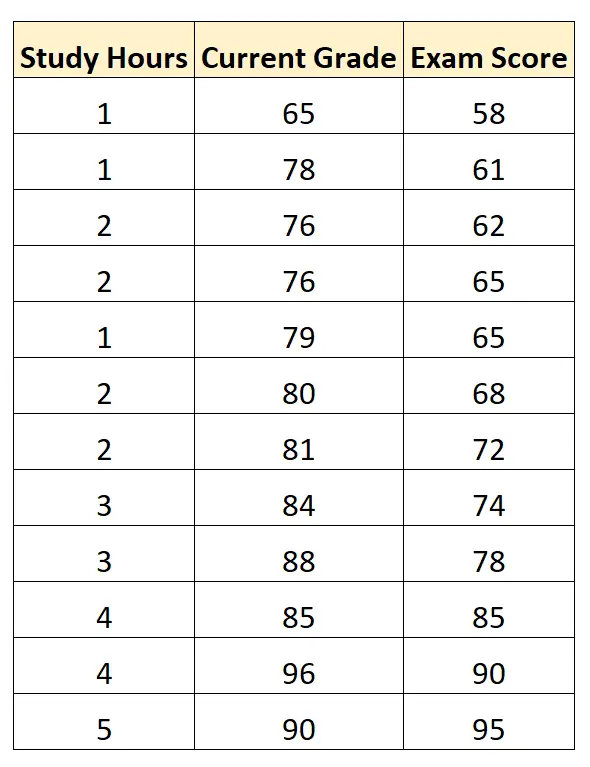
使用统计软件，我们可以使用“学习时间”和“当前成绩”作为预测变量，“考试成绩”作为响应变量来拟合多元线性回归模型。

我们可以找到该模型的以下输出：

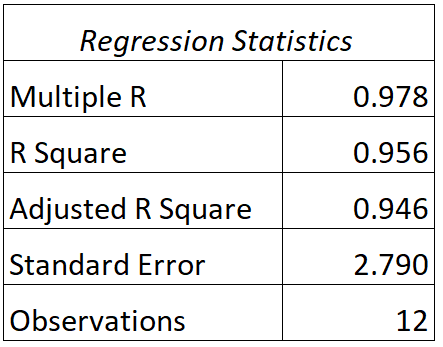
以下是如何解释该模型的 R 和 R 平方值：

• 答：实际测试分数与模型预测测试分数之间的相关性为0.978 。
• R ² ：该回归模型的 R 平方为0.956 。这告诉我们，95.6% 的考试成绩差异可以通过学习时数和学生当前在班级的成绩来解释。

另请注意，R ²值仅等于 R 值的平方：

^R2 = R * R = 0.978 * 0.978 = 0.956

其他资源

什么是好的 R 平方值？
平方和简单指南：SST、SSR、SSE