如何在 r 中计算 dfbetas

在统计学中，我们经常想知道不同的观察结果对回归模型有何影响。

计算观测值影响的一种方法是使用称为DFBETAS 的度量，它告诉我们删除每个单独观测值对每个系数的标准化影响。

这个指标让我们了解每个观测值对给定回归模型中每个系数估计的影响。

本教程展示了如何计算和可视化 R 模型中每个观测值的 DFBETAS 的分步示例。

第 1 步：创建回归模型

首先，我们将使用 R 中内置的mtcars数据集创建一个多元线性回归模型：

 #fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

步骤 2：计算每个观测值的 DFBETAS

接下来，我们将使用内置的dfbetas()函数来计算模型中每个观测值的 DFBETAS 值：

 #calculate DFBETAS for each observation in the model
dfbetas <- as . data . frame (dfbetas(model))

#display DFBETAS for each observation
dfbetas

                      (Intercept) disp hp
Mazda RX4 -0.1174171253 0.030760632 1.748143e-02
Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02
Datsun 710 -0.1694989349 0.086630144 -3.332781e-05
Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02
Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01
Valiant -0.1711908285 -0.139135639 1.829038e-01
Duster 360 -0.0312338677 -0.005356209 3.581378e-02
Merc 240D -0.0312259577 -0.010409922 2.433256e-02
Merc 230 -0.0865872595 0.016428917 2.287867e-02
Merc 280 -0.1560683502 0.078667906 -1.911180e-02
Merc 280C -0.2254489597 0.113639937 -2.760800e-02
Merc 450SE 0.0022844093 0.002966155 -2.855985e-02
Merc 450SL 0.0009062022 0.001176644 -1.132941e-02
Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02
Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02
Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02
Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02
Fiat 128 0.5720358325 -0.181104179 -1.265475e-01
Honda Civic 0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona -0.2181110386 0.101336902 5.945352e-03
Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02
AMC Javelin -0.0406785103 -0.141711468 1.074514e-01
Camaro Z28 0.0390139262 0.012846225 -5.031588e-02
Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01
Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa 0.3444562478 -0.402678927 2.135224e-01
Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01
Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01
Maserati Bora -0.3436265545 -0.511285637 7.319066e-01
Volvo 142E -0.1784974091 0.132692956 -4.433915e-02

对于每个观测值，我们可以看到当我们删除该特定观测值时，原点、 disp变量和hp变量的系数估计值之间的差异。

一般来说，如果观测值的 DBETAS 值大于阈值 2/√ n （其中n是观测值的数量），我们认为该观测值对给定系数的估计有很大影响。

在此示例中，阈值将为0.3535534 ：

 #find number of observations
n <- nrow (mtcars)

#calculate DFBETAS threshold value
thresh <- 2/ sqrt (n)

thresh

[1] 0.3535534

第 3 步：可视化 DFBETAS

最后，我们可以创建绘图来可视化模型中每个观测值和每个预测变量的 DFBETAS 值：

 #specify 2 rows and 1 column in plotting region
by(mfrow=c(2,1))

#plot DFBETAS for disp with threshold lines
plot(dfbetas$disp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

#plot DFBETAS for hp with threshold lines 
plot(dfbetas$hp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

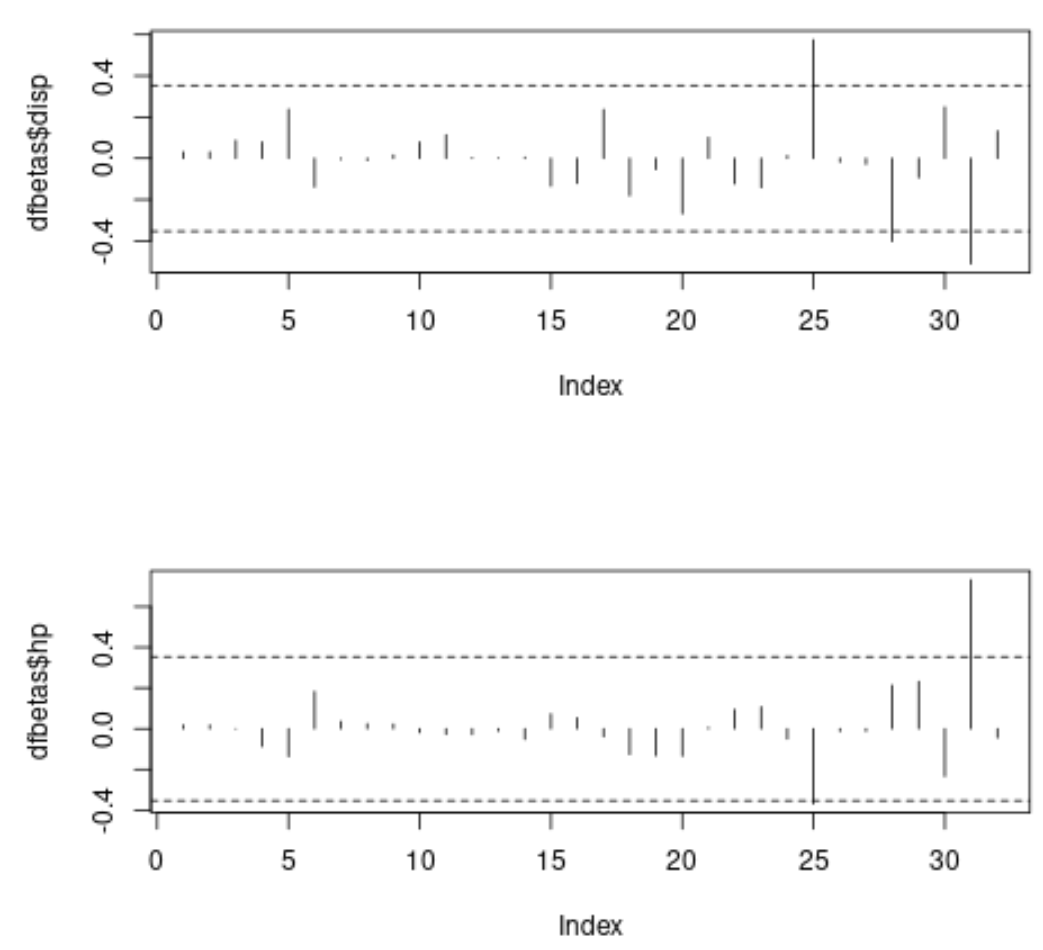
在每个图中，x 轴显示数据集中每个观测值的索引，y 值显示每个观测值和每个预测变量对应的 DFBETAS。

在第一个图中，我们可以看到三个观测值超过了绝对阈值0.3535534 ，在第二个图中，我们可以看到两个观测值超过了绝对阈值。

我们可以选择更仔细地研究这些观察结果，以确定它们是否对模型系数的估计产生不当影响。

其他资源

如何在 R 中执行简单线性回归
如何在 R 中执行多元线性回归
如何在 R 中计算杠杆统计数据
如何在 R 中计算 DFFITS