如何在 r 中计算偏度和峰度

在统计学中，偏度和峰度是测量分布形状的两种方法。

偏度是分布偏度的度量。该值可以是正值，也可以是负值。

• 负偏度表示尾部位于分布的左侧，向更多负值延伸。
• 正偏度表示尾部位于分布的右侧，向更正的值延伸。
• 值为零表示分布不存在不对称性，这意味着分布完全对称。

峰度是衡量分布与正态分布相比是重尾还是轻尾的指标。

• 正态分布的峰度为 3。
• 如果给定分布的峰度小于 3，则称其为playkurtic ，这意味着与正态分布相比，它往往会产生更少且不太极端的异常值。
• 如果给定分布的峰度大于 3，则称为尖峰分布，这意味着它往往会比正态分布产生更多的异常值。

注意：某些公式（Fisher 定义）会从峰度中减去 3，以便更容易与正态分布进行比较。使用此定义，如果分布的峰度值大于 0，则该分布的峰度将大于正态分布。

本教程介绍如何在 R 中计算给定数据集的偏度和峰度。

示例：R 中的偏度和扁平化

假设我们有以下数据集：

 data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)

我们可以通过创建直方图来快速可视化该数据集中值的分布：

 hist(data, col=' steelblue ') 

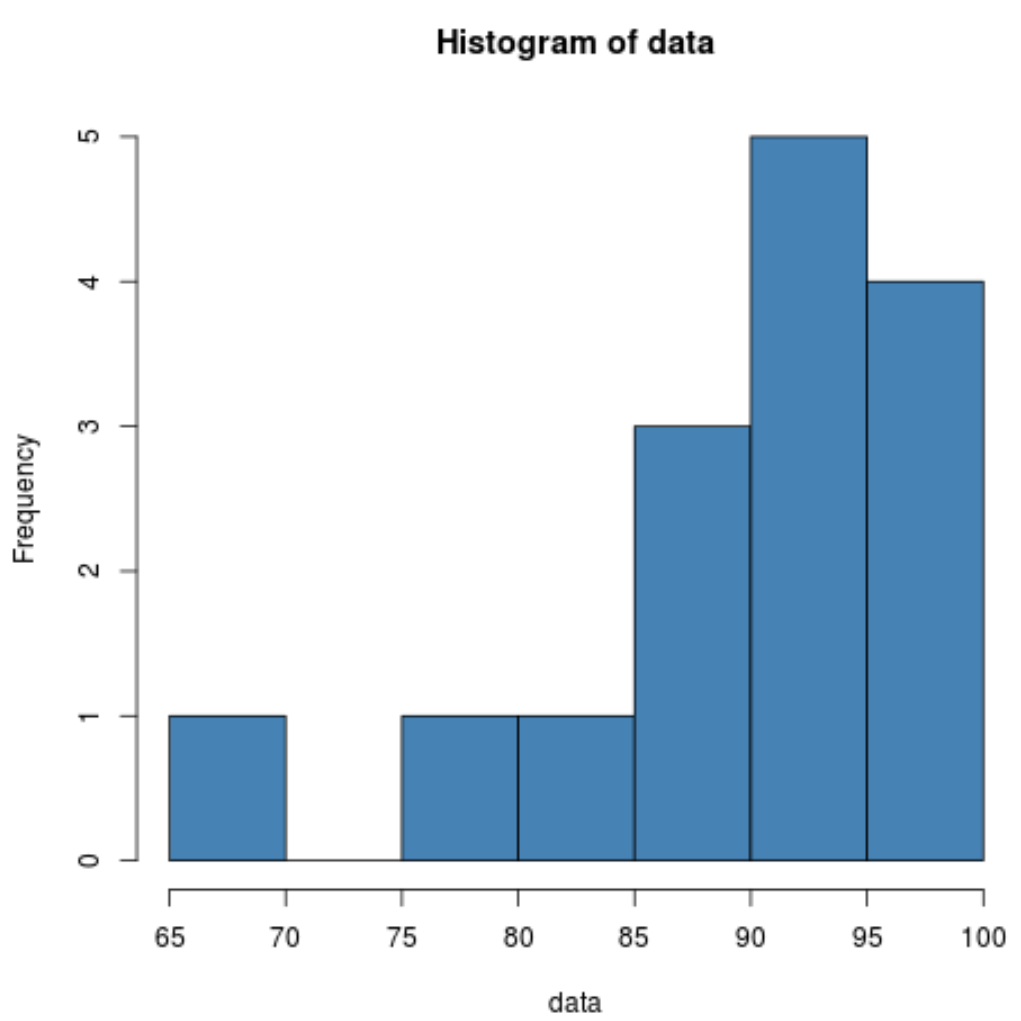
直方图向我们表明分布似乎向左倾斜。也就是说，较大部分的值集中在分布的右侧。

为了计算该数据集的偏度和峰度，我们可以使用 R 中矩库中的skewness()和kurtosis()函数：

 library (moments)

#calculate skewness
skewness(data)

[1] -1.391777

#calculate kurtosis
kurtosis(data)

[1] 4.177865

偏度结果为-1.391777 ，峰度结果为4.177865 。

由于偏度为负，这表明分布是左偏的。这证实了我们在直方图中看到的内容。

由于峰度大于 3，这表明与正态分布相比，该分布尾部有更多值。

moment库还提供jarque.test()函数，该函数执行拟合优度测试，确定样本数据是否表现出与正态分布一致的偏度和峰度。该检验的原假设和备择假设如下：

零假设：数据集具有与正态分布相对应的偏度和峰度。

替代假设：数据集具有不符合正态分布的偏斜和峰度。

以下代码显示了如何执行此测试：

 jarque.test(data)

	Jarque-Bera Normality Test

data:data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater

测试的 p 值为0.05756 。由于该值不小于 α = 0.05，因此我们无法拒绝原假设。我们没有足够的证据表明该数据集具有与正态分布不同的偏度和峰度。

您可以在此处找到完整的Moments库文档。

奖励：偏度和峰度计算器

您还可以使用统计偏度和峰度计算器来计算给定数据集的偏度，该计算器会自动计算给定数据集的偏度和峰度。