如何在 r 中执行分段回归（逐步）

分段回归是当数据集中存在明确的“断点”时我们经常使用的回归方法。

以下分步示例展示了如何在 R 中执行分段回归。

第 1 步：创建数据

首先，我们创建以下数据框：

 #view DataFrame
df <- data. frame (x=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16),
                 y=c(2, 4, 5, 6, 8, 10, 12, 13, 15, 19, 24, 28, 31, 34, 39, 44))

#view first six rows of data frame
head(df)

  xy
1 1 2
2 2 4
3 3 5
4 4 6
5 5 8
6 6 10

第 2 步：可视化数据

接下来，让我们创建一个散点图来可视化数据：

 #create scatterplot of x vs. y
plot(df$x, df$y, pch= 16 , col=' steelblue ')

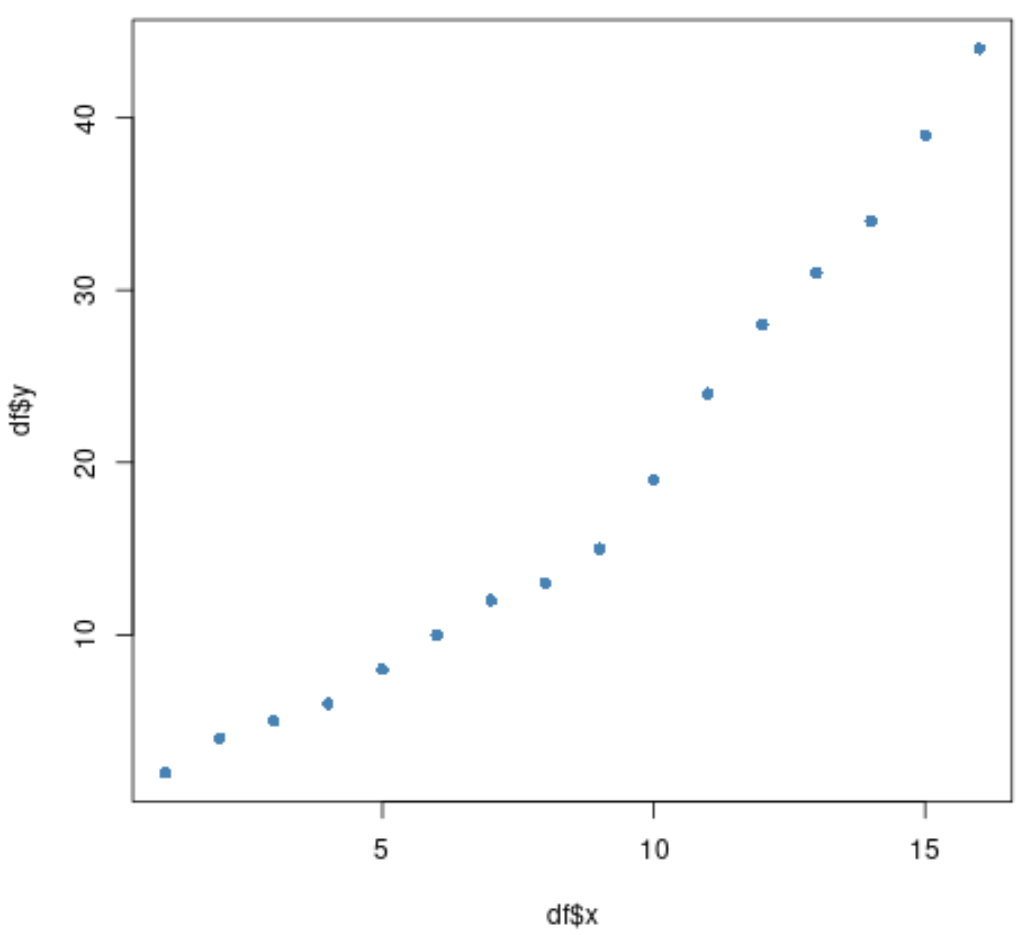
我们可以看到 x 和 y 之间的关系似乎在x = 9附近突然发生变化。

步骤 3：拟合分段回归模型

我们可以使用R中segmented包中的segmented()函数来将分段回归模型拟合到我们的数据集：

 library (segmented)

#fit simple linear regression model
fit <- lm(y ~ x, data=df)

#fit piecewise regression model to original model, estimating a breakpoint at x=9
segmented. fit <- segmented(fit, seg.Z = ~x, psi= 9 )

#view summary of segmented model
summary( segmented.fit )

Call: 
segmented.lm(obj = fit, seg.Z = ~x, psi = 9)

Estimated Break-Point(s):
         East. St.Err
psi1.x 8.762 0.26

Meaningful coefficients of the linear terms:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.32143 0.48343 0.665 0.519    
x 1.59524 0.09573 16.663 1.16e-09 ***
U1.x 2.40476 0.13539 17.762 NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.6204 on 12 degrees of freedom
Multiple R-Squared: 0.9983, Adjusted R-squared: 0.9978 

Convergence achieved in 2 iter. (rel. changes 0)

segmented()函数在 x = 8.762 处检测到断点。

拟合的分段回归模型为：

如果 x ≤ 8.762：y = 0.32143 + 1.59524*(x)

如果 x > 8.762： y = 0.32143 + 1.59524*(8.762) + (1.59524+2.40476)*(x-8.762)

例如，假设我们的值为x = 5 。估计值为：

• y = 0.32143 + 1.59524*(x)
• y = 0.32143 + 1.59524*(5)
• y = 8.297

或者假设我们的值为x = 12 。估计值为：

• y = 0.32143 + 1.59524*(8.762) + (1.59524+2.40476)*(12-8.762)
• y = 27.25

步骤 4：可视化最终的分段回归模型

我们可以使用以下代码在原始数据之上可视化最终的分段回归模型：

 #plot original data
plot(df$x, df$y, pch= 16 , col=' steelblue ')

#add segmented regression model
plot(segmented. fit , add= T )

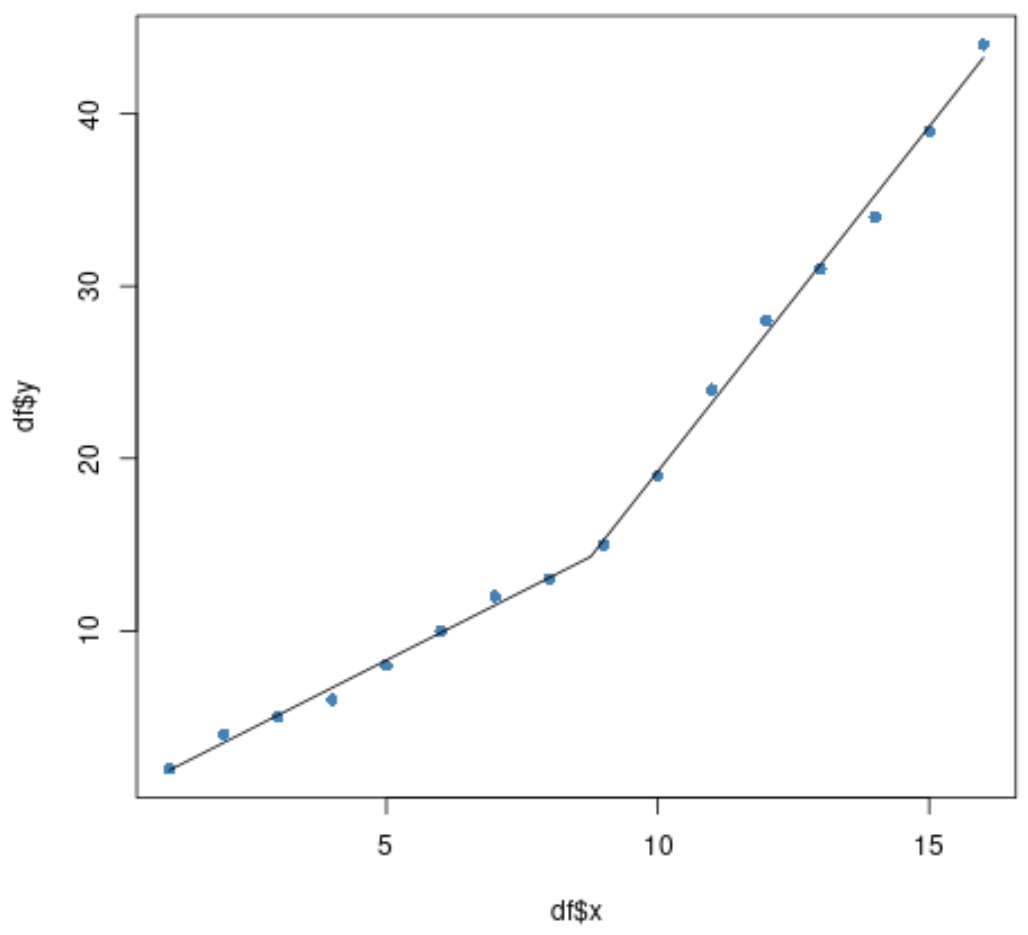
看来分段回归模型与数据拟合得很好。

其他资源

以下教程提供有关 R 回归模型的其他信息：

如何在 R 中执行简单线性回归
如何在 R 中执行多元线性回归
如何在 R 中执行逻辑回归
如何在 R 中执行分位数回归
如何在 R 中执行加权回归