如何在 r 中拟合分类树和回归树

当一组预测变量和响应变量之间的关系是线性时，多元线性回归等方法可以生成准确的预测模型。

然而，当一组预测变量和响应之间的关系更加复杂时，非线性方法通常可以生成更准确的模型。

其中一种方法是 分类和回归树(CART)，它使用一组预测变量来创建预测响应变量值的决策树。

如果响应变量是连续的，我们可以构建回归树，如果响应变量是分类的，我们可以构建分类树。

本教程介绍如何在 R 中创建回归树和分类树。

示例 1：在 R 中构建回归树

在本例中，我们将使用ISLR包中的Hitters数据集，其中包含 263 名职业棒球运动员的各种信息。

我们将使用此数据集构建一个回归树，该回归树使用本垒打和打球年份的预测变量来预测给定球员的薪水。

使用以下步骤创建此回归树。

步骤1：加载必要的包。

首先，我们将加载此示例所需的包：

 library (ISLR) #contains Hitters dataset
library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

步骤 2：构建初始回归树。

首先，我们将构建一个大型的初始回归树。我们可以通过使用较小的cp值（代表“复杂度参数”）来保证树很大。

这意味着只要模型的整体 R 平方至少增加 cp 指定的值，我们就会对回归树执行进一步的分割。

然后我们将使用printcp()函数打印模型结果：

 #build the initial tree
tree <- rpart(Salary ~ Years + HmRun, data=Hitters, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] HmRun Years

Root node error: 53319113/263 = 202734

n=263 (59 observations deleted due to missingness)

           CP nsplit rel error xerror xstd
1 0.24674996 0 1.00000 1.00756 0.13890
2 0.10806932 1 0.75325 0.76438 0.12828
3 0.01865610 2 0.64518 0.70295 0.12769
4 0.01761100 3 0.62652 0.70339 0.12337
5 0.01747617 4 0.60891 0.70339 0.12337
6 0.01038188 5 0.59144 0.66629 0.11817
7 0.01038065 6 0.58106 0.65697 0.11687
8 0.00731045 8 0.56029 0.67177 0.11913
9 0.00714883 9 0.55298 0.67881 0.11960
10 0.00708618 10 0.54583 0.68034 0.11988
11 0.00516285 12 0.53166 0.68427 0.11997
12 0.00445345 13 0.52650 0.68994 0.11996
13 0.00406069 14 0.52205 0.68988 0.11940
14 0.00264728 15 0.51799 0.68874 0.11916
15 0.00196586 16 0.51534 0.68638 0.12043
16 0.00016686 17 0.51337 0.67577 0.11635
17 0.00010000 18 0.51321 0.67576 0.11615
n=263 (59 observations deleted due to missingness)

第三步：修剪树。

接下来，我们将修剪回归树，以找到用于 cp（复杂性参数）的最佳值，从而实现最低的测试误差。

请注意，cp 的最佳值是导致前一输出中x 误差最低的值，它表示交叉验证数据的观测值的误差。

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

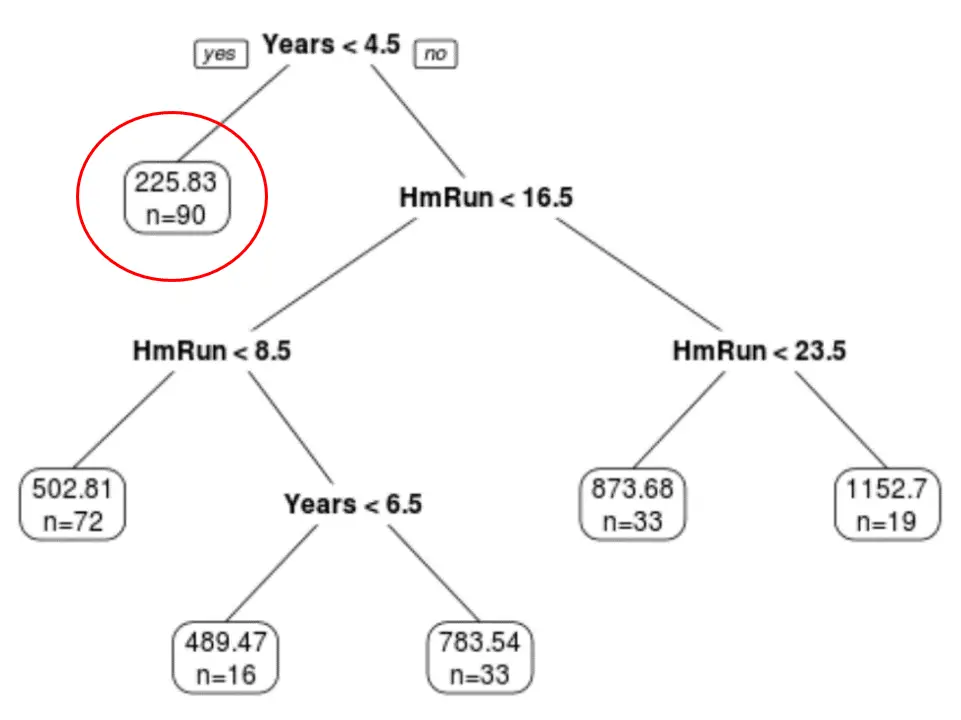
我们可以看到最终的修剪树有六个终端节点。每个叶节点显示该节点中球员的预测工资以及原始数据集中属于该级别的观察数。

例如，我们可以看到，在原始数据集中，有 90 名经验不足 4.5 年的球员，他们的平均工资为 $225.83K。

第四步：使用树进行预测。

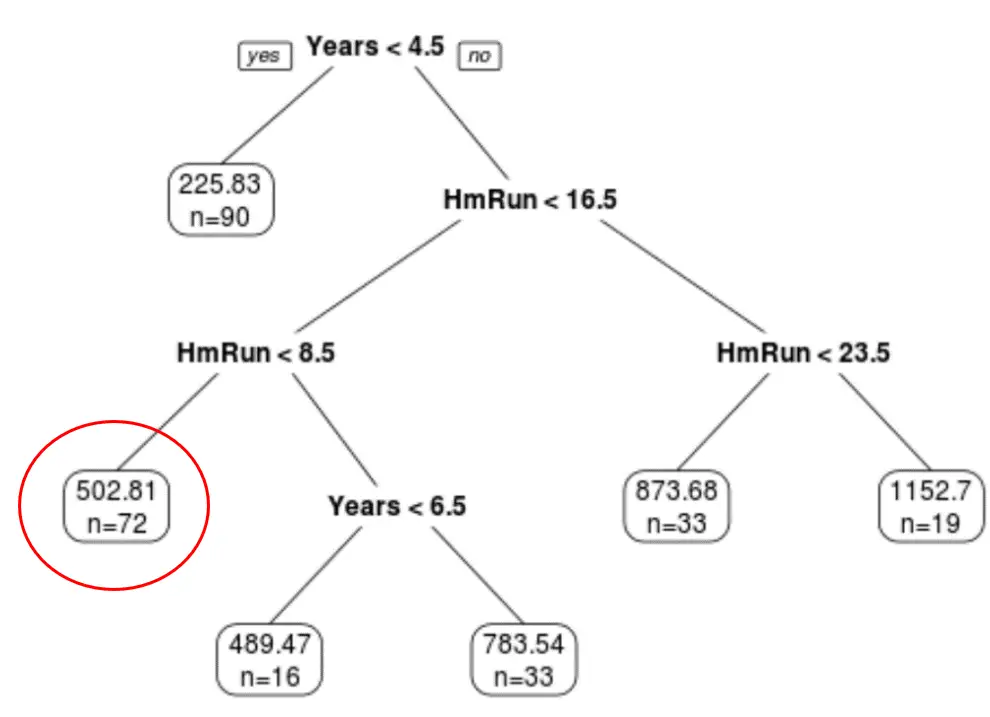
我们可以使用最终的修剪树来根据给定球员的多年经验和平均本垒打来预测他的薪水。

例如，一名拥有 7 年经验、平均打出 4 个本垒打的球员，其预期薪资为$502.81k 。

我们可以使用R中的predict()函数来确认这一点：

 #define new player
new <- data.frame(Years=7, HmRun=4)

#use pruned tree to predict salary of this player
predict(pruned_tree, newdata=new)

502.8079

示例 2：在 R 中构建分类树

在本例中，我们将使用rpart.plot包中的ptitanic数据集，其中包含有关泰坦尼克号上乘客的各种信息。

我们将使用此数据集创建一个分类树，该分类树使用预测变量类、性别和年龄来预测给定乘客是否幸存。

使用以下步骤创建此分类树。

步骤1：加载必要的包。

首先，我们将加载此示例所需的包：

 library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

步骤2：构建初始分类树。

首先，我们将构建一个大型的初始分类树。我们可以通过使用较小的cp值（代表“复杂度参数”）来保证树很大。

这意味着只要整体模型拟合度至少增加 cp 指定的值，我们就会对分类树执行进一步的分割。

然后我们将使用printcp()函数打印模型结果：

 #build the initial tree
tree <- rpart(survived~pclass+sex+age, data=ptitanic, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] age pclass sex   

Root node error: 500/1309 = 0.38197

n=1309 

      CP nsplit rel error xerror xstd
1 0.4240 0 1.000 1.000 0.035158
2 0.0140 1 0.576 0.576 0.029976
3 0.0095 3 0.548 0.578 0.030013
4 0.0070 7 0.510 0.552 0.029517
5 0.0050 9 0.496 0.528 0.029035
6 0.0025 11 0.486 0.532 0.029117
7 0.0020 19 0.464 0.536 0.029198
8 0.0001 22 0.458 0.528 0.029035

第三步：修剪树。

接下来，我们将修剪回归树，以找到用于 cp（复杂性参数）的最佳值，从而实现最低的测试误差。

请注意，cp 的最佳值是导致前一输出中x 误差最低的值，它表示交叉验证数据的观测值的误差。

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

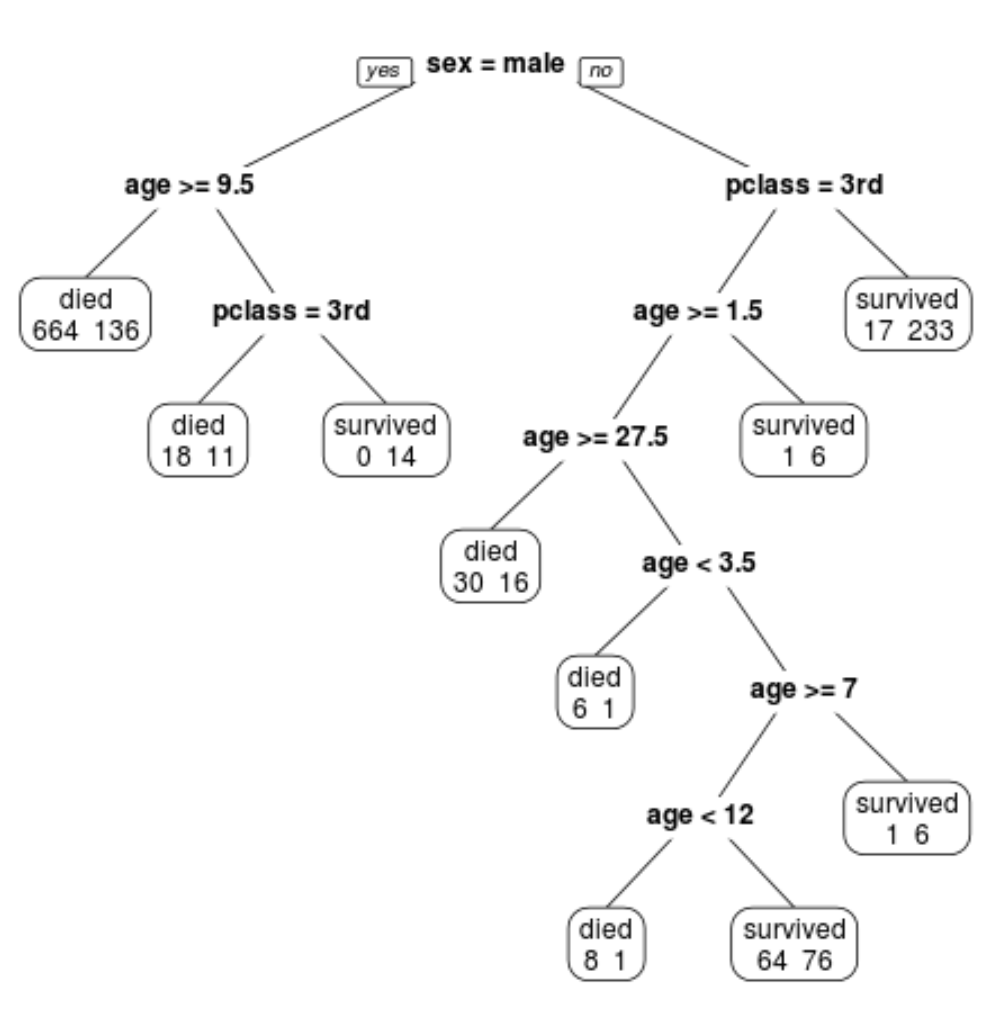
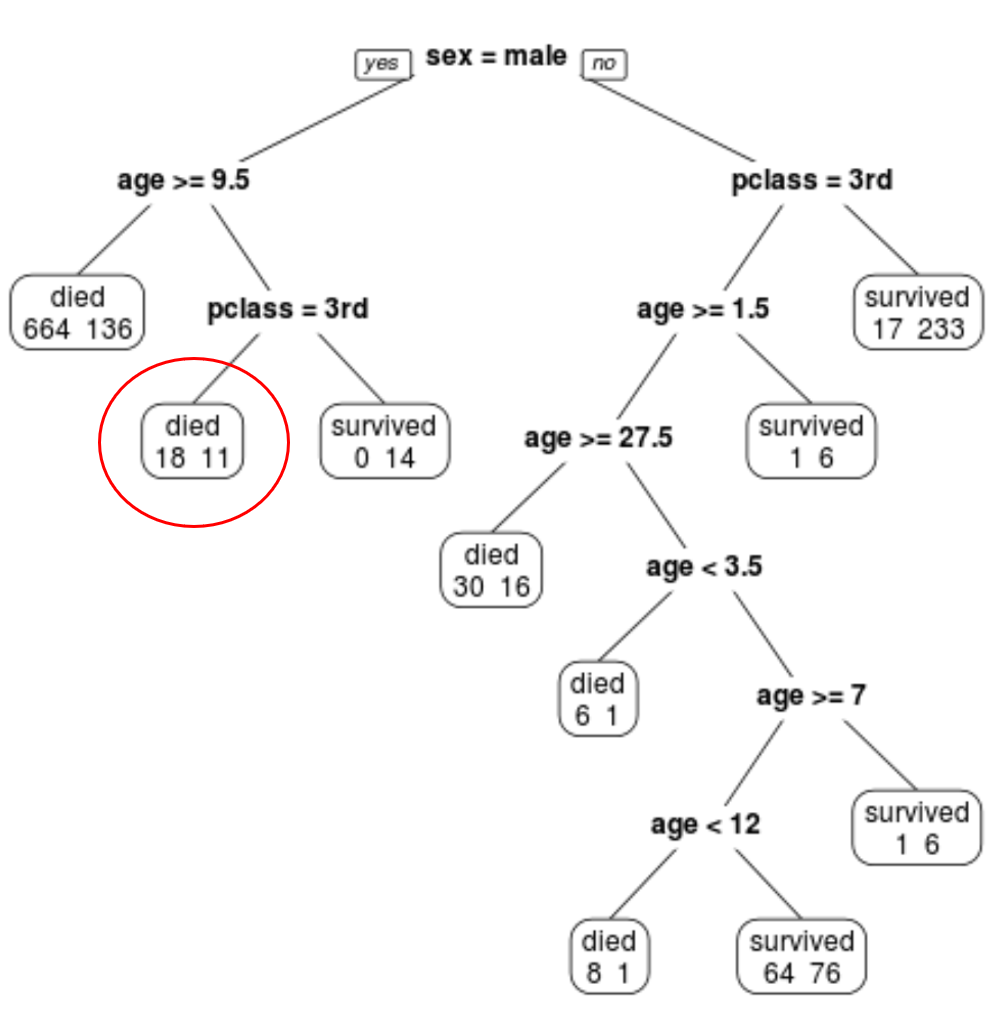
我们可以看到最终的剪枝树有 10 个终端节点。每个航站楼节点都显示死亡乘客人数以及幸存者人数。

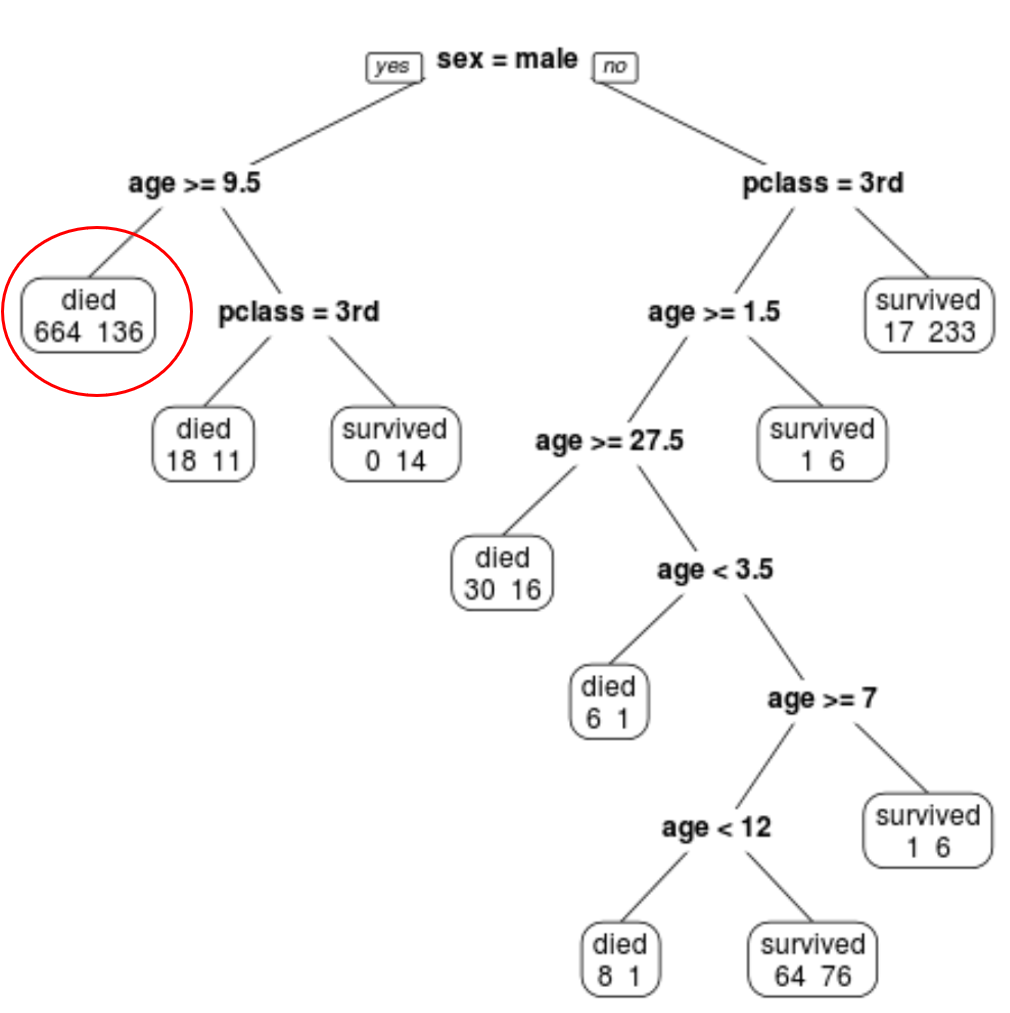
例如，在最左边的节点中，我们看到 664 名乘客死亡，136 名乘客幸存。

第四步：使用树进行预测。

我们可以使用最终的修剪树来根据乘客的类别、年龄和性别来预测特定乘客的生存概率。

例如，一名 8 岁的一等舱男性乘客的生存概率为 11/29 = 37.9%。

您可以在此处找到这些示例中使用的完整 R 代码。