如何计算 r 中的加权标准差

当数据集中的某些值比其他值具有更高的权重时，加权标准差是衡量数据集中值的分散性的有用方法。

加权标准差的计算公式为：

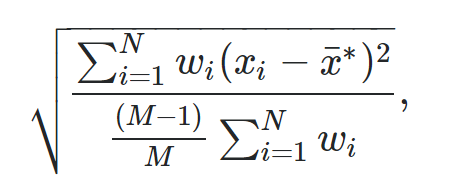
金子：

• N：观察总数
• M：非零权重的数量
• w _i ：权重向量
• x _i ：数据值向量
• x ：加权平均值

在 R 中计算加权标准差的最简单方法是使用Hmisc包中的wt.var()函数，该函数使用以下语法：

 #define data values
x <- c(4, 7, 12, 13, ...)

#define weights
wt <- c(.5, 1, 2, 2, ...)

#calculate weighted variance
weighted_var <- wtd. var (x, wt)

#calculate weighted standard deviation
weighted_sd <- sqrt(weighted_var)

以下示例展示了如何在实践中使用此功能。

示例 1：向量的加权标准差

以下代码显示了如何计算 R 中单个向量的加权标准差：

 library (Hmisc)

#define data values 
x <- c(14, 19, 22, 25, 29, 31, 31, 38, 40, 41)

#define weights
wt <- c(1, 1, 1.5, 2, 2, 1.5, 1, 2, 3, 2)

#calculate weighted variance 
weighted_var <- wtd. var (x, wt)

#calculate weighted standard deviation
sqrt(weighted_var)

[1] 8.570051

加权标准差为8.57 。

示例 2：数据框中某列的加权标准差

以下代码显示了如何计算 R 中数据帧的列的加权标准差：

 library (Hmisc)

#define data frame
df <- data. frame (team=c('A', 'A', 'A', 'A', 'A', 'B', 'B', 'C'),
                 wins=c(2, 9, 11, 12, 15, 17, 18, 19),
                 dots=c(1, 2, 2, 2, 3, 3, 3, 3))

#define weights
wt <- c(1, 1, 1.5, 2, 2, 1.5, 1, 2)

#calculate weighted standard deviation of points
sqrt(wtd. var (df$points, wt))

[1] 0.6727938

点列的加权标准差为0.673 。

示例 3：数据框中多列的加权标准差

以下代码演示如何使用 R 中的sapply()函数计算数据框中多列的加权标准差：

 library (Hmisc)

#define data frame
df <- data. frame (team=c('A', 'A', 'A', 'A', 'A', 'B', 'B', 'C'),
                 wins=c(2, 9, 11, 12, 15, 17, 18, 19),
                 dots=c(1, 2, 2, 2, 3, 3, 3, 3))

#define weights
wt <- c(1, 1, 1.5, 2, 2, 1.5, 1, 2)

#calculate weighted standard deviation of points and wins
sapply(df[c(' wins ', ' points ')], function(x) sqrt(wtd. var (x, wt)))

     win points 
4.9535723 0.6727938 

胜利列的加权标准差为4.954 ，得分列的加权标准差为0.673 。

其他资源

如何在 Excel 中计算加权标准差
如何计算 R 中的标准差
如何计算R的变异系数
如何计算R中的范围