如何在 r 中引导（带有示例）

Bootstrapping是一种可用于估计任何统计量的标准误差并生成统计量的置信区间的方法。

bootstrapping的基本流程如下：

• 从给定的数据集中取出k 个具有替换的重复样本。
• 对于每个样本，计算感兴趣的统计量。
• 这为给定统计量提供了k 个不同的估计值，然后您可以使用这些估计值来计算统计量的标准误差并为统计量创建置信区间。

我们可以使用bootstrap 库中的以下函数在 R 中进行引导：

1. 生成引导样本。

启动（数据、统计、R、…）

金子：

• 数据：向量、矩阵或数据块
• 统计：生成要启动的统计数据的函数
• A：引导重复次数

2. 生成引导置信区间。

boot.ci（启动对象、conf、类型）

金子：

• bootobject： boot()函数返回的对象
• conf：要计算的置信区间。默认值为 0.95
• type：要计算的置信区间类型。选项包括“标准”、“基本”、“螺柱”、“perc”、“bca”和“全部” – 默认为“全部”

以下示例展示了如何在实践中使用这些功能。

示例 1：引导单个统计数据

以下代码显示如何计算简单线性回归模型的R 平方的标准误差：

 set.seed(0)
library (boot)

#define function to calculate R-squared
rsq_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (summary(fit)$r.square) #return R-squared of model
}
#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=rsq_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = rsq_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
     original bias std. error
t1* 0.7183433 0.002164339 0.06513426

从结果我们可以看出：

• 该回归模型的估计 R 平方为0.7183433 。
• 此估计的标准误差为0.06513426 。

我们还可以快速可视化引导样本的分布：

 plot(reps)

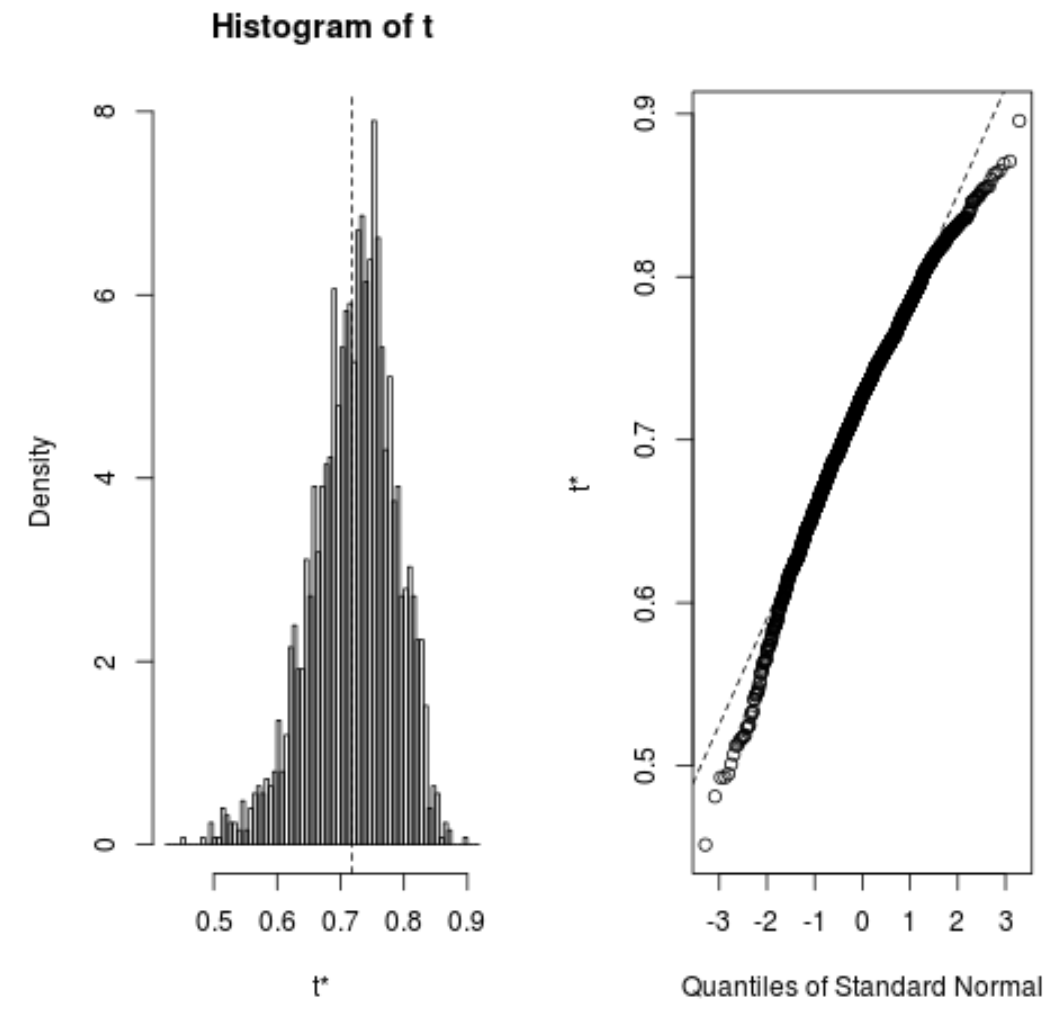
我们还可以使用以下代码来计算模型估计 R 平方的 95% 置信区间：

 #calculate adjusted bootstrap percentile (BCa) interval
boot.ci(reps, type=" bca ")

CALL: 
boot.ci(boot.out = reps, type = "bca")

Intervals: 
Level BCa          
95% (0.5350, 0.8188)  
Calculations and Intervals on Original Scale

从结果中我们可以看出，真实 R 平方值的自举 95% 置信区间为 (0.5350, 0.8188)。

示例2：引导多重统计

以下代码显示如何计算多元线性回归模型中每个系数的标准误差：

 set.seed(0)
library (boot)

#define function to calculate fitted regression coefficients
coef_function <- function (formula, data, indices) {
  d <- data[indices,] #allows boot to select sample
  fit <- lm(formula, data=d) #fit regression model
  return (coef(fit)) #return coefficient estimates of model
}

#perform bootstrapping with 2000 replications
reps <- boot(data=mtcars, statistic=coef_function, R=2000, formula=mpg~disp)

#view results of boostrapping
reps

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = mtcars, statistic = coef_function, R = 2000, formula = mpg ~ 
    available)


Bootstrap Statistics:
       original bias std. error
t1* 29.59985476 -5.058601e-02 1.49354577
t2* -0.04121512 6.549384e-05 0.00527082

从结果我们可以看出：

• 模型截距的估计系数为29.59985476 ，该估计的标准误差为1.49354577 。
• 模型中预测变量disp的估计系数为-0.04121512 ，该估计值的标准误差为0.00527082 。

我们还可以快速可视化引导样本的分布：

 plot(reps, index=1) #intercept of model
plot(reps, index=2) #disp predictor variable

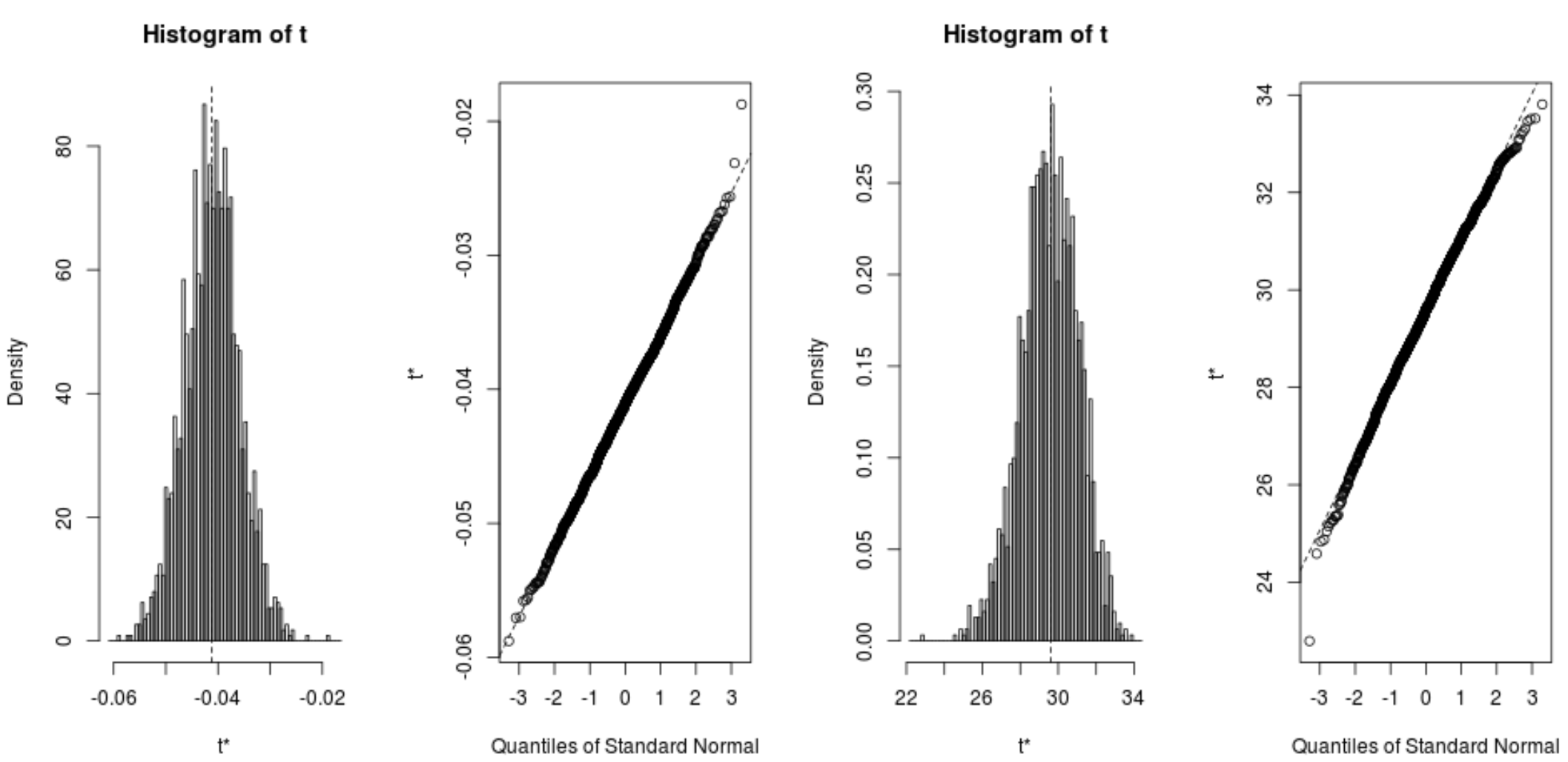
我们还可以使用以下代码来计算每个系数的 95% 置信区间：

 #calculate adjusted bootstrap percentile (BCa) intervals
boot.ci(reps, type=" bca ", index=1) #intercept of model
boot.ci(reps, type=" bca ", index=2) #disp predictor variable

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 1)

Intervals: 
Level BCa          
95% (26.78, 32.66)  
Calculations and Intervals on Original Scale
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 2000 bootstrap replicates

CALL: 
boot.ci(boot.out = reps, type = "bca", index = 2)

Intervals: 
Level BCa          
95% (-0.0520, -0.0312)  
Calculations and Intervals on Original Scale

从结果中我们可以看到模型系数的 bootstrap 95% 置信区间如下：

• 拦截IC：(26.78, 32.66)
• 显示CI：(-.0520，-.0312)

其他资源

如何在 R 中执行简单线性回归
如何在 R 中执行多元线性回归
置信区间简介