如何在 r 中计算抽样分布

抽样分布是基于来自单个总体的许多随机样本的特定统计量的概率分布。

本教程介绍如何在 R 中使用采样分布执行以下操作：

• 生成抽样分布。
• 可视化样本分布。
• 计算抽样分布的平均值和标准差。
• 计算有关抽样分布的概率。

在 R 中生成抽样分布

以下代码展示了如何在 R 中生成抽样分布：

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656

在此示例中，我们使用rnorm()函数计算 10,000 个样本的平均值，其中每个样本大小为 20，并根据平均值为 5.3、标准差为 9 的正态分布生成。

我们可以看到第一个样本的平均值为 5.283992，第二个样本的平均值为 6.304845，依此类推。

可视化样本分布

以下代码展示了如何创建简单的直方图来可视化采样分布：

 #create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

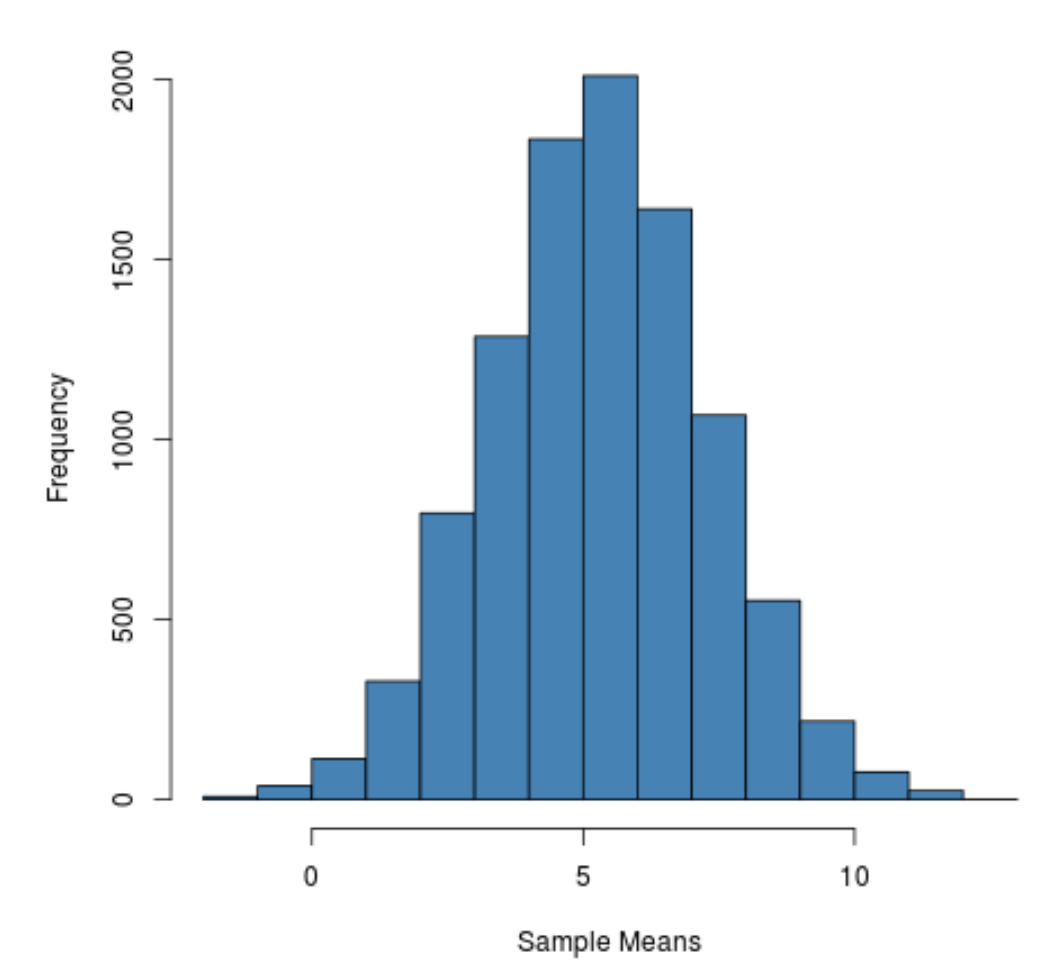
可以看出，采样分布呈钟形，峰值位于值 5 附近。

然而，从分布的尾部我们可以看到，一些样本的均值大于 10，而另一些样本的均值小于 0。

求平均值和标准差

下面的代码展示了如何计算样本分布的均值和标准差：

 #mean of sampling distribution
mean(sample_means)

[1] 5.287195

#standard deviation of sampling distribution
sd(sample_means)

[1] 2.00224

理论上，抽样分布的均值应为 5.3。我们可以看到，本例中的实际样本均值是5.287195 ，接近 5.3。

理论上，抽样分布的标准差应该等于 s/√n，即 9 / √20 = 2.012。我们可以看到，抽样分布的实际标准差是2.00224 ，接近 2.012。

计算概率

以下代码显示了在给定总体平均值、总体标准差和样本大小的情况下，如何计算获得样本平均值的特定值的概率。

 #calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

在此特定示例中，假设总体平均值为 5.3、总体标准差为 9、样本大小为 20 为0.6417 ，我们发现样本平均值小于或等于 6 的概率。

这与采样分布计算器计算的概率非常接近：

完整代码

本例中使用的完整R代码如下所示：

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

#mean of sampling distribution
mean(sample_means)

#standard deviation of sampling distribution
sd(sample_means)

#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

其他资源

抽样分布简介
抽样分布计算器
中心极限定理简介