如何在 r 中计算杠杆统计数据
在统计学中,如果某个观测值的响应变量值远大于数据集中的其他观测值,则该观测值被视为异常值。
同样,如果某个观测值具有一个或多个与数据集中其他观测值相比更为极端的预测变量值,则该观测值被视为高杠杆。
任何类型的分析的第一步都是仔细研究具有高影响力的观察结果,因为它们可能对给定模型的结果产生很大影响。
本教程展示了如何计算和可视化 R 模型中每个观察的杠杆率的分步示例。
第 1 步:创建回归模型
首先,我们将使用 R 中内置的mtcars数据集创建一个多元线性回归模型:
#load the dataset data(mtcars) #fit a regression model model <- lm(mpg~disp+hp, data=mtcars) #view model summary summary(model) Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 30.735904 1.331566 23.083 < 2nd-16 *** available -0.030346 0.007405 -4.098 0.000306 *** hp -0.024840 0.013385 -1.856 0.073679 . --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.127 on 29 degrees of freedom Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09
第 2 步:计算每个观察的杠杆率
接下来,我们将使用hatvalues()函数来计算模型中每个观察的杠杆率:
#calculate leverage for each observation in the model hats <- as . data . frame (hatvalues(model)) #display leverage stats for each observation hats hatvalues(model) Mazda RX4 0.04235795 Mazda RX4 Wag 0.04235795 Datsun 710 0.06287776 Hornet 4 Drive 0.07614472 Hornet Sportabout 0.08097817 Valiant 0.05945972 Duster 360 0.09828955 Merc 240D 0.08816960 Merc 230 0.05102253 Merc 280 0.03990060 Merc 280C 0.03990060 Merc 450SE 0.03890159 Merc 450SL 0.03890159 Merc 450SLC 0.03890159 Cadillac Fleetwood 0.19443875 Lincoln Continental 0.16042361 Chrysler Imperial 0.12447530 Fiat 128 0.08346304 Honda Civic 0.09493784 Toyota Corolla 0.08732818 Toyota Corona 0.05697867 Dodge Challenger 0.06954069 AMC Javelin 0.05767659 Camaro Z28 0.10011654 Pontiac Firebird 0.12979822 Fiat X1-9 0.08334018 Porsche 914-2 0.05785170 Lotus Europa 0.08193899 Ford Pantera L 0.13831817 Ferrari Dino 0.12608583 Maserati Bora 0.49663919 Volvo 142E 0.05848459
通常,我们会仔细研究杠杆值大于 2 的观测值。
执行此操作的一个简单方法是根据观测值的杠杆值按降序对观测值进行排序:
#sort observations by leverage, descending hats[ order (-hats[' hatvalues(model) ']), ] [1] 0.49663919 0.19443875 0.16042361 0.13831817 0.12979822 0.12608583 [7] 0.12447530 0.10011654 0.09828955 0.09493784 0.08816960 0.08732818 [13] 0.08346304 0.08334018 0.08193899 0.08097817 0.07614472 0.06954069 [19] 0.06287776 0.05945972 0.05848459 0.05785170 0.05767659 0.05697867 [25] 0.05102253 0.04235795 0.04235795 0.03990060 0.03990060 0.03890159 [31] 0.03890159 0.03890159
我们可以看到最高杠杆值为0.4966 。由于这个数字不大于 2,我们知道数据集中的所有观测值都没有高杠杆率。
第 3 步:可视化每个观察结果的杠杆作用
最后,我们可以创建一个快速图表来可视化每个观察的杠杆率:
#plot leverage values for each observation plot(hatvalues(model), type = ' h ')
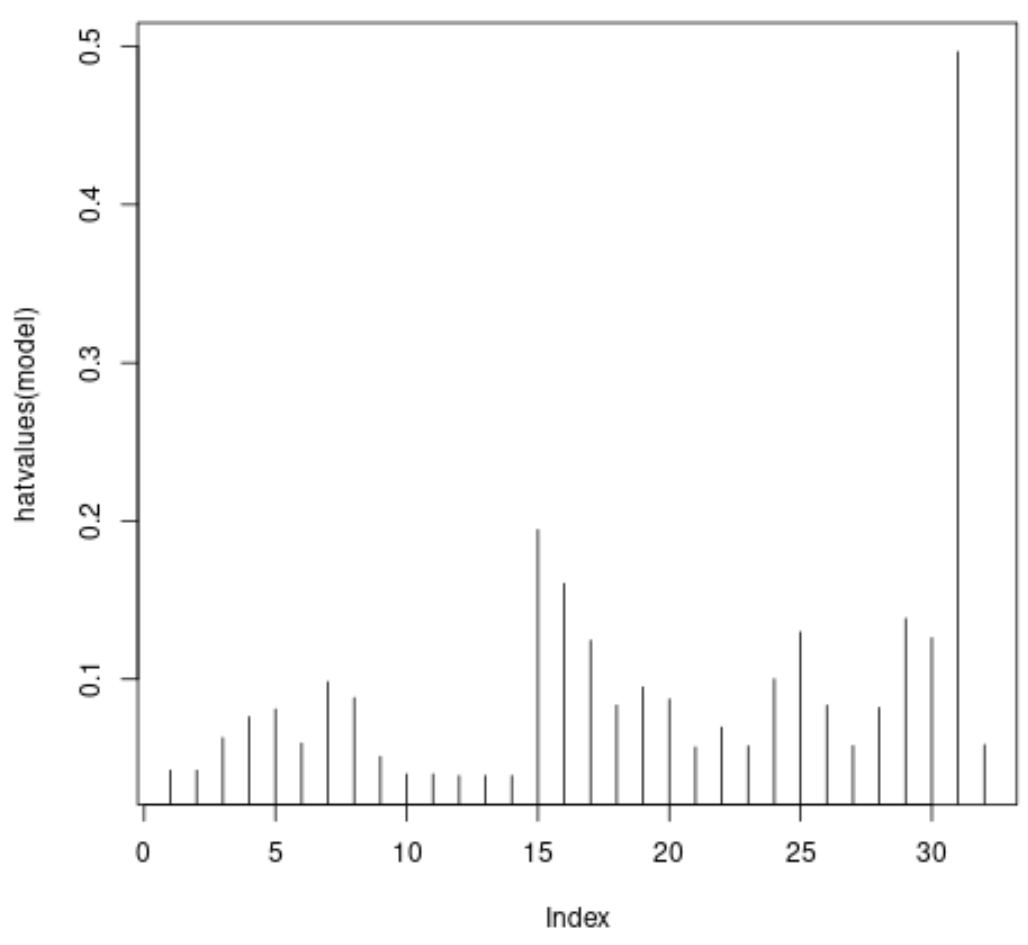
x 轴显示数据集中每个观测值的索引,y 值显示每个观测值相应的杠杆统计数据。