如何在 r 中执行 scheffe 测试

单向方差分析用于确定三个或更多独立组的平均值之间是否存在统计显着差异。

如果方差分析表的总体p 值低于一定的显着性水平，则我们有足够的证据表明至少其中一个组均值与其他均值不同。

然而，这并没有告诉我们哪些群体彼此不同。这只是告诉我们并非所有组的平均值都是相等的。

为了准确地知道哪些组彼此不同，我们需要执行事后测试来控制每个族的错误率。

最常用的事后检验之一是 Scheffe 检验。

本教程介绍如何在 R 中执行 Scheffe 测试。

示例：R 中的 Scheffe 测试

假设老师想知道三种不同的学习技巧是否会导致学生的考试成绩不同。为了测试这一点，她随机分配 10 名学生使用每种学习技巧并记录他们的考试结果。

我们可以使用 R 中的以下步骤来拟合单向方差分析，以测试三组之间平均考试成绩的差异，并使用 Scheffe 测试来准确确定哪些组不同。

步骤 1：创建数据集。

以下代码演示了如何创建包含所有 30 名学生的考试结果的数据集：

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

第 2 步：查看每组的考试结果。

以下代码显示如何生成箱线图以可视化每组考试结果的分布：

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

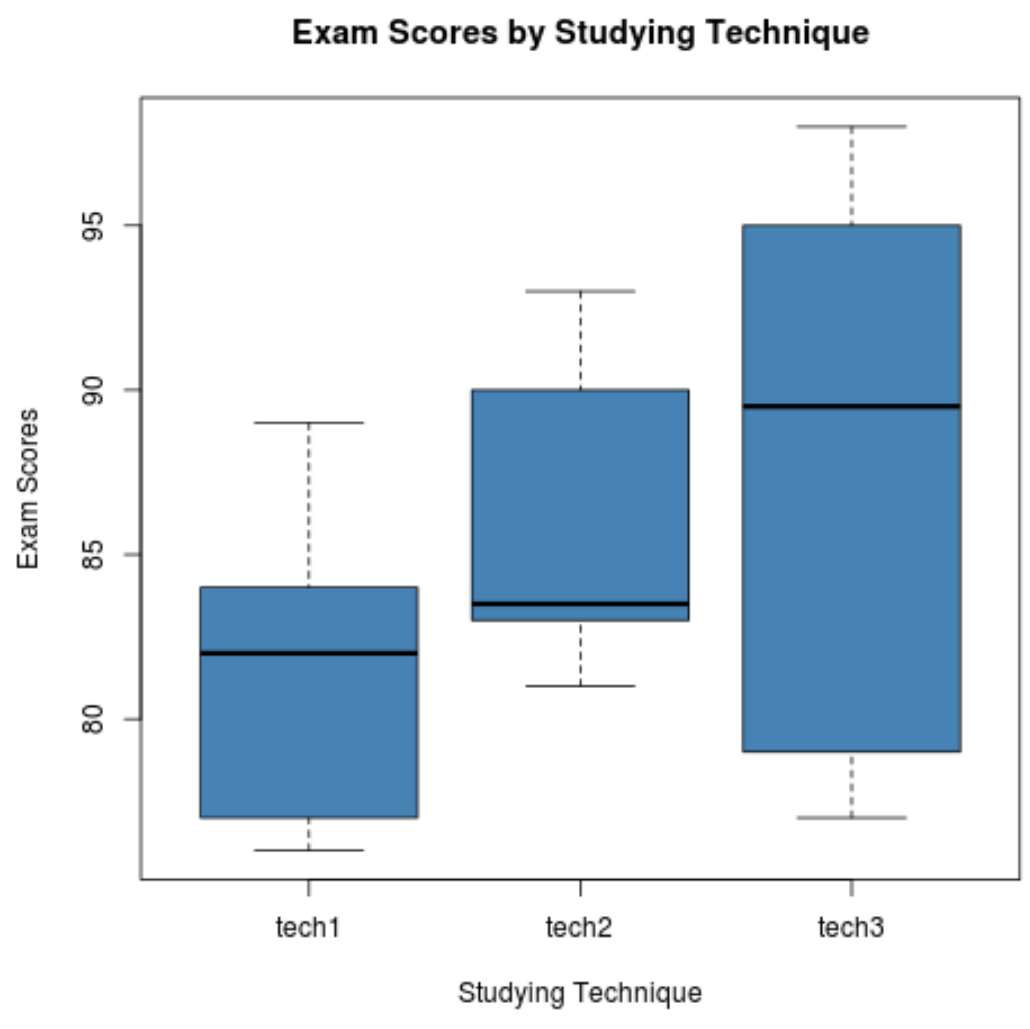
步骤 3：执行单向方差分析。

以下代码显示如何执行单向方差分析来测试每组平均考试成绩之间的差异：

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

由于总体 p 值 ( 0.0476 ) 小于 0.05，这表明每个组的平均考试成绩不同。

接下来，我们将执行 Scheffe 测试来确定哪些组是不同的。

步骤 4：执行 Scheffe 测试。

为了执行 Scheffe 测试，我们将使用DescTools包中的ScheffeTest()函数。

以下代码展示了如何在我们的示例中使用此函数：

 #load DescTools package
library(DescTools)

#perform Scheffe's test
ScheffeTest(model)

  Posthoc multiple comparisons of means: Scheffe Test 
    95% family-wise confidence level

$technical
            diff lwr.ci upr.ci pval    
tech2-tech1 4.2 -2.24527202 10.645272 0.2582    
tech3-tech1 6.4 -0.04527202 12.845272 0.0519 .  
tech3-tech2 2.2 -4.24527202 8.645272 0.6803    

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

结果解释方式如下：

• 技术 2 和技术 1 之间的考试成绩平均差异为4.2 。平均差的相应 p 值为0.2582 。
• 技术 3 和技术 1 之间的考试成绩平均差异为6.4 。平均差的相应 p 值为0.0519 。
• 技术 3 和技术 2 之间的考试成绩平均差异为2.2 。平均差的相应 p 值为0.6803 。

根据我们决定使用的显着性水平，唯一在统计上显着不同的两组是技术 3 和技术 1。

其他资源

如何在 R 中执行单向方差分析
如何在 R 中执行 Tukey 测试
如何在 R 中执行 Bonferroni 校正