如何在 r 中执行简单线性回归（逐步）

简单线性回归是一种我们可以用来理解单个解释变量和单个响应变量之间关系的技术。

简而言之，该技术找到一条最“适合”数据的线，并采用以下形式：

ŷ = b ₀ + b ₁ x

金子：

• ŷ : 估计响应值
• b ₀ ：回归线的原点
• b ₁ ：回归线的斜率

该方程可以帮助我们理解解释变量和响应变量之间的关系，并且（假设它具有统计显着性）它可以用于在给定解释变量值的情况下预测响应变量的值。

本教程逐步说明如何在 R 中执行简单线性回归。

第 1 步：加载数据

对于此示例，我们将为 15 名学生创建一个包含以下两个变量的假数据集：

• 某些考试的学习总小时数
• 考试成绩

我们将尝试使用小时数作为解释变量、检查结果作为响应变量来拟合一个简单的线性回归模型。

以下代码展示了如何在 R 中创建这个假数据集：

 #create dataset
df <- data.frame(hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of dataset
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

#attach dataset to make it more convenient to work with
attach(df)

第 2 步：可视化数据

在拟合简单的线性回归模型之前，我们必须首先将数据可视化以理解它。

首先，我们要确保小时和分数之间的关系近似线性，因为这是简单线性回归的一个巨大的 基本假设。我们可以创建一个简单的散点图来可视化两个变量之间的关系：

 scatter.smooth(hours, score, main=' Hours studied vs. Exam Score ')

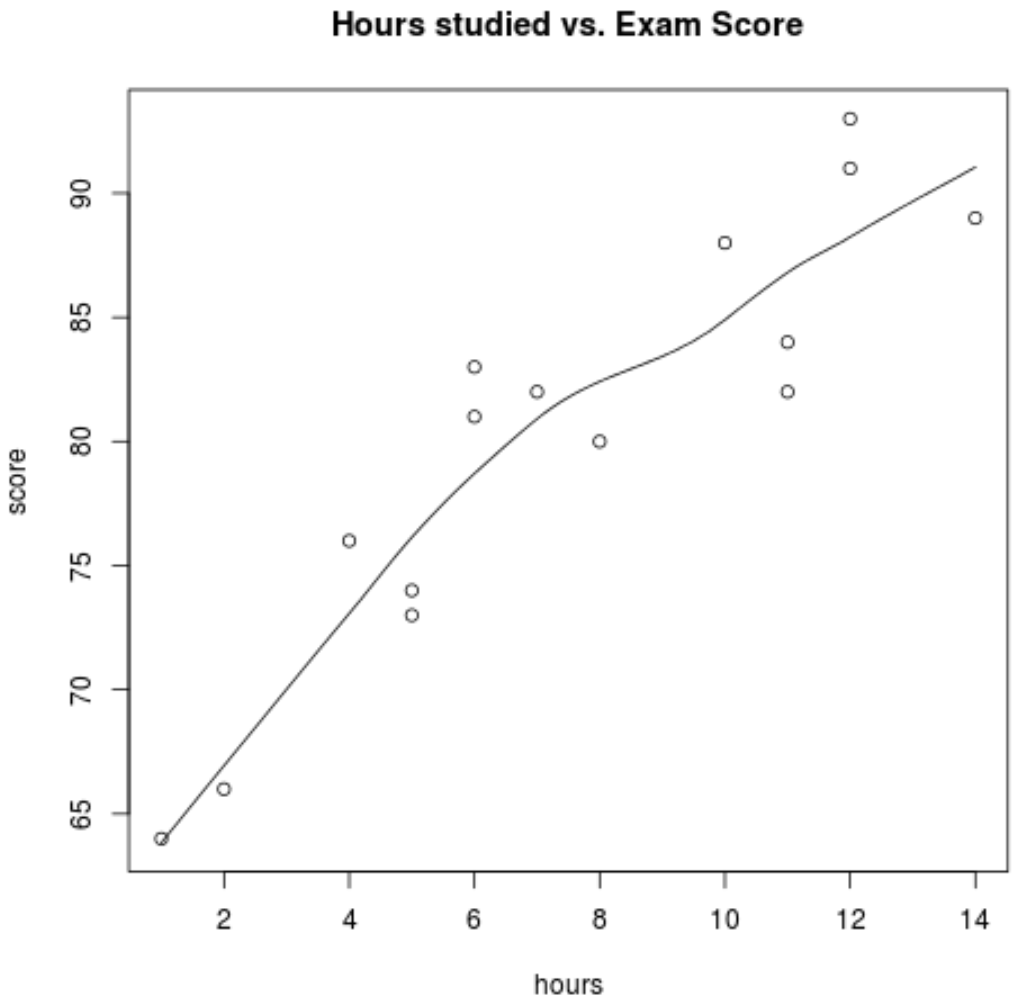
从图中我们可以看出，这种关系似乎是线性的。随着小时数的增加，分数也趋于线性增加。

然后我们可以创建一个箱线图来可视化考试结果的分布并检查异常值。默认情况下，如果观测值是第三四分位 (Q3) 上方四分位距的 1.5 倍或第一四分位 (Q1) 下方四分位距的 1.5 倍，则 R 将观测值定义为离群值。

如果观察值异常，箱线图中会出现一个小圆圈：

 boxplot(score) 

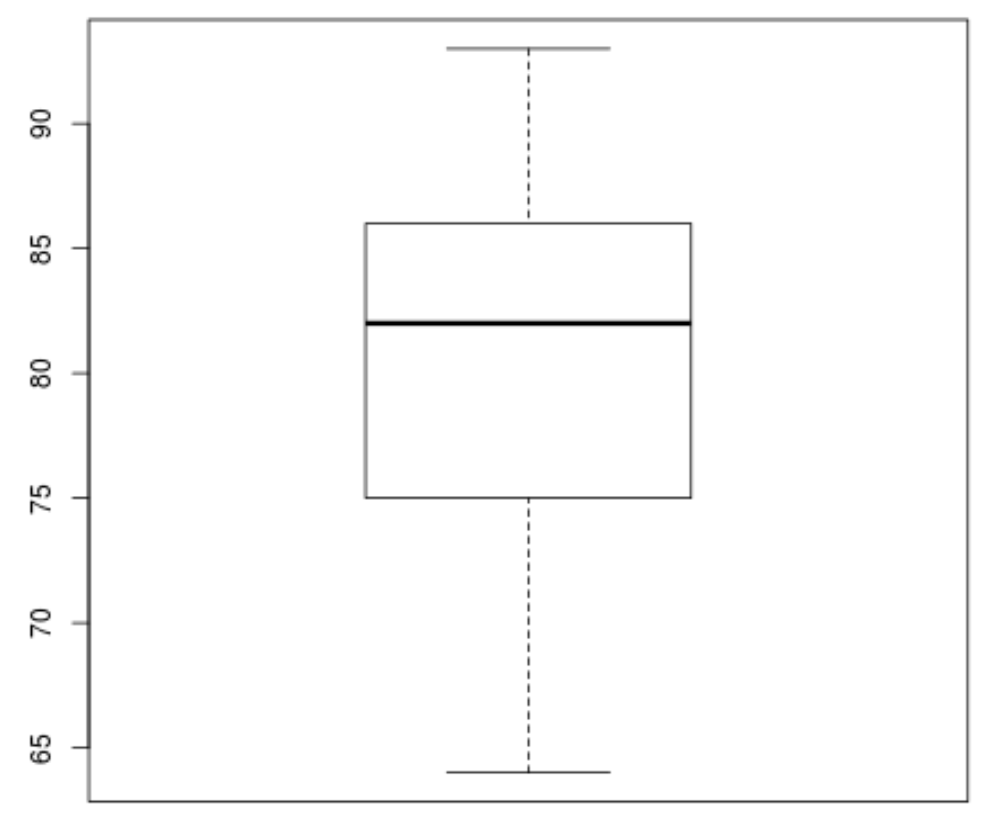
箱线图中没有小圆圈，这意味着我们的数据集中没有异常值。

步骤 3：执行简单的线性回归

一旦我们确认变量之间的关系是线性的并且不存在异常值，我们就可以继续使用小时作为解释变量和分数作为响应变量来拟合一个简单的线性回归模型：

 #fit simple linear regression model
model <- lm(score~hours)

#view model summary
summary(model)

Call:
lm(formula = score ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

从模型总结中我们可以看出，拟合的回归方程为：

分数 = 65.334 + 1.982*（小时）

这意味着每多学习一小时，平均考试成绩就会增加1,982分。原始值65,334告诉我们零学习时间的学生的平均预期考试成绩。

我们还可以使用这个方程根据学生学习的小时数找到预期的考试成绩。例如，学习 10 小时的学生应获得85.15的考试成绩：

分数 = 65.334 + 1.982*(10) = 85.15

以下是如何解释模型摘要的其余部分：

• Pr(>|t|)：这是与模型系数相关的 p 值。由于小时数(2.25e-06) 的 p 值显着小于 0.05，因此我们可以说小时数和分数之间存在统计上显着的关联。
• 多重 R 平方：这个数字告诉我们，考试成绩的变化百分比可以用学习的小时数来解释。一般来说，回归模型的 R 平方值越大，解释变量越能预测响应变量的值。在这种情况下， 83.1%的分数差异可以用学习时间来解释。
• 残差标准误差：这是观测值与回归线之间的平均距离。该值越低，回归线越能与观察到的数据相对应。在这种情况下，考试中观察到的平均分数与回归线预测的分数相差3,641分。
• F 统计量和 p 值： F 统计量 ( 63.91 ) 和相应的 p 值 ( 2.253e-06 ) 告诉我们回归模型的整体显着性，即模型中的解释变量是否有助于解释变异。在响应变量中。由于此示例中的 p 值小于 0.05，因此我们的模型具有统计显着性，并且小时数被认为有助于解释分数变化。

第 4 步：创建残差图

将简单线性回归模型拟合到数据后，最后一步是创建残差图。

线性回归的关键假设之一是回归模型的残差近似正态分布，并且在解释变量的每个水平上都是同方差的。如果不满足这些假设，我们的回归模型的结果可能会产生误导或不可靠。

为了验证是否满足这些假设，我们可以创建以下残差图：

残差与拟合值图：该图对于确认同方差性很有用。 x 轴显示拟合值，y 轴显示残差。只要残差看起来在零值周围随机且均匀地分布在整个图中，我们就可以假设不违反同方差性：

 #define residuals
res <- resid(model)

#produce residual vs. fitted plot
plot(fitted(model), res)

#add a horizontal line at 0 
abline(0,0)

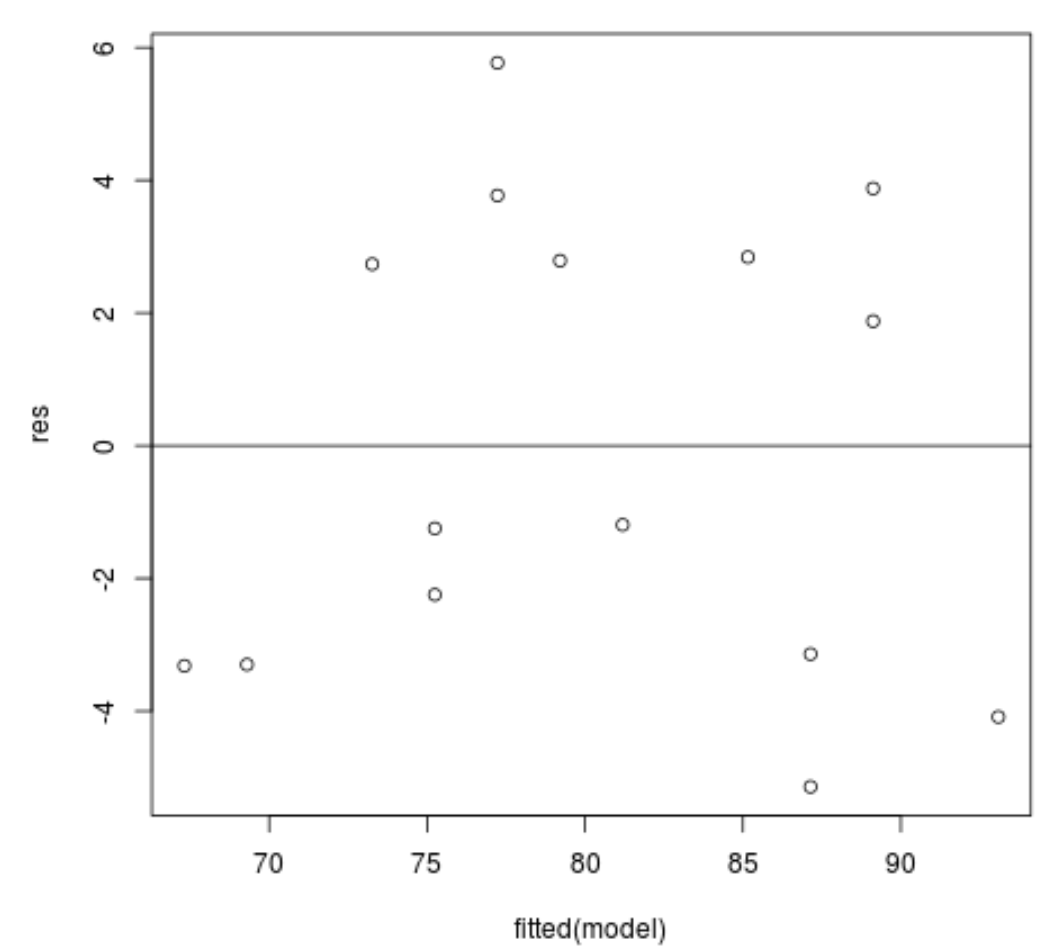
残差似乎随机分散在零附近，并且没有显示出明显的模式，因此满足此假设。

QQ 图：该图可用于确定残差是否服从正态分布。如果图中的数据值大致呈 45 度角直线分布，则数据呈正态分布：

 #create QQ plot for residuals
qqnorm(res)

#add a straight diagonal line to the plot
qqline(res) 

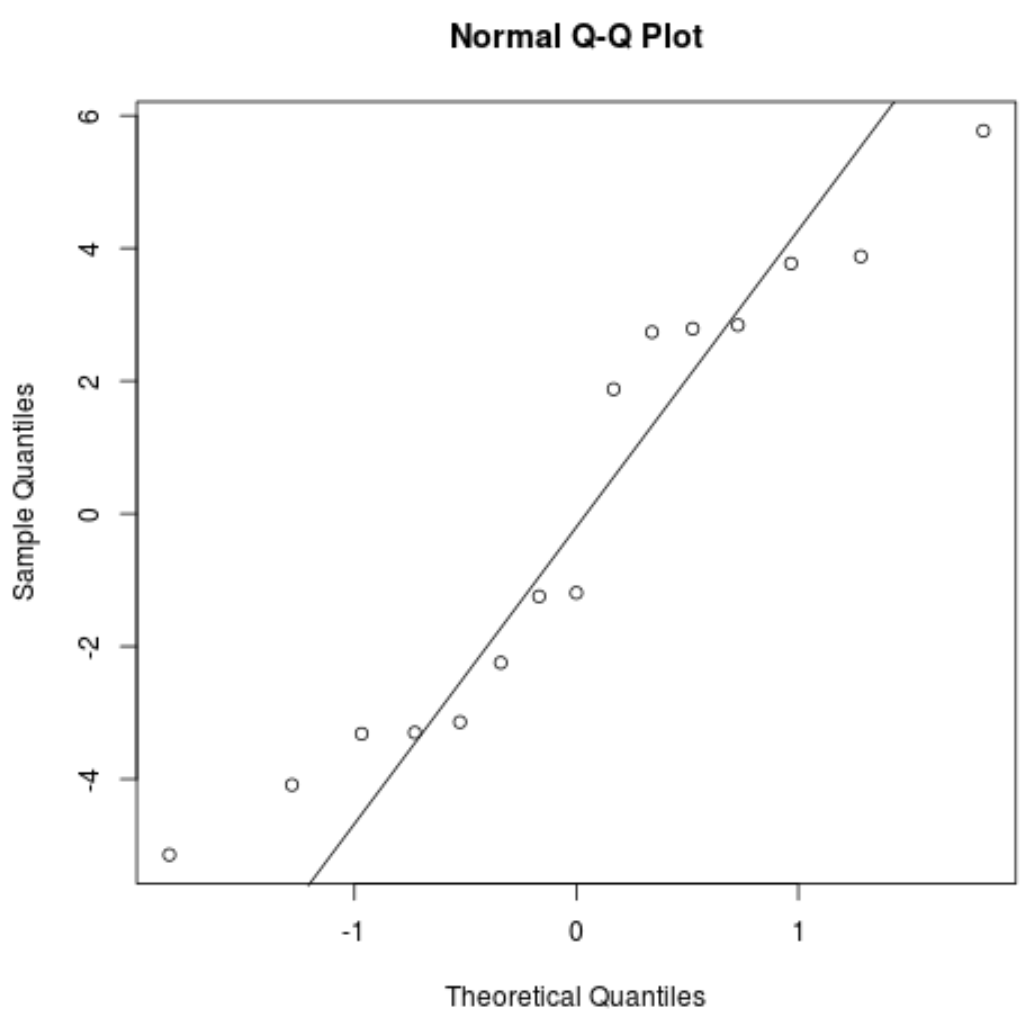
残差稍微偏离 45 度线，但不足以引起严重关注。我们可以假设满足正态性假设。

由于残差呈正态分布且同方差，我们验证了简单线性回归模型的假设得到满足。因此，我们模型的输出是可靠的。

本教程中使用的完整 R 代码可以在此处找到。