如何解释 r 中的诊断图
线性回归模型用于描述一个或多个预测变量与响应变量之间的关系。
然而,一旦我们拟合了回归模型,最好还生成诊断图来分析模型残差并确保线性模型适合我们正在处理的特定数据。
本教程介绍如何在 R 中创建和解释给定回归模型的诊断图。
示例:在 R 中创建和解释诊断图
假设我们使用“学习时间”拟合一个简单的线性回归模型来预测某个班级学生的“考试成绩”:
#create data frame df <- data. frame (hours=c(1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6), score=c(67, 65, 68, 77, 73, 79, 81, 88, 80, 67, 84, 93, 90, 91)) #fit linear regression model model = lm(score ~ hours, data=df)
我们可以使用plot()命令为该回归模型生成四个诊断图:
#produce diagnostic plots for regression model
plot(model)
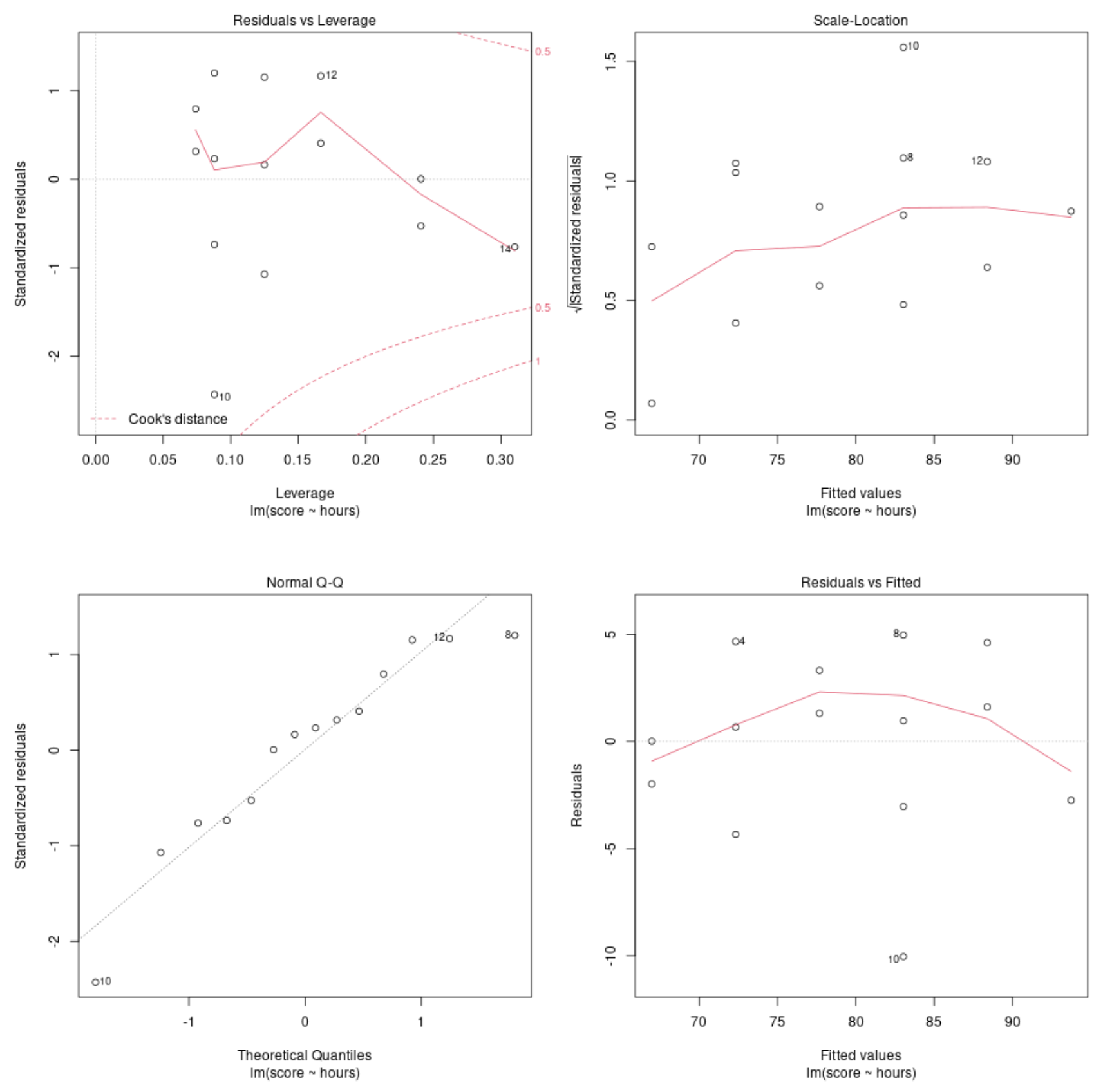
诊断图#1:残差与残差杠杆图
该图用于识别有影响力的观察结果。如果该图上的任何点落在库克距离(虚线)之外,那么这是一个有影响力的观察。
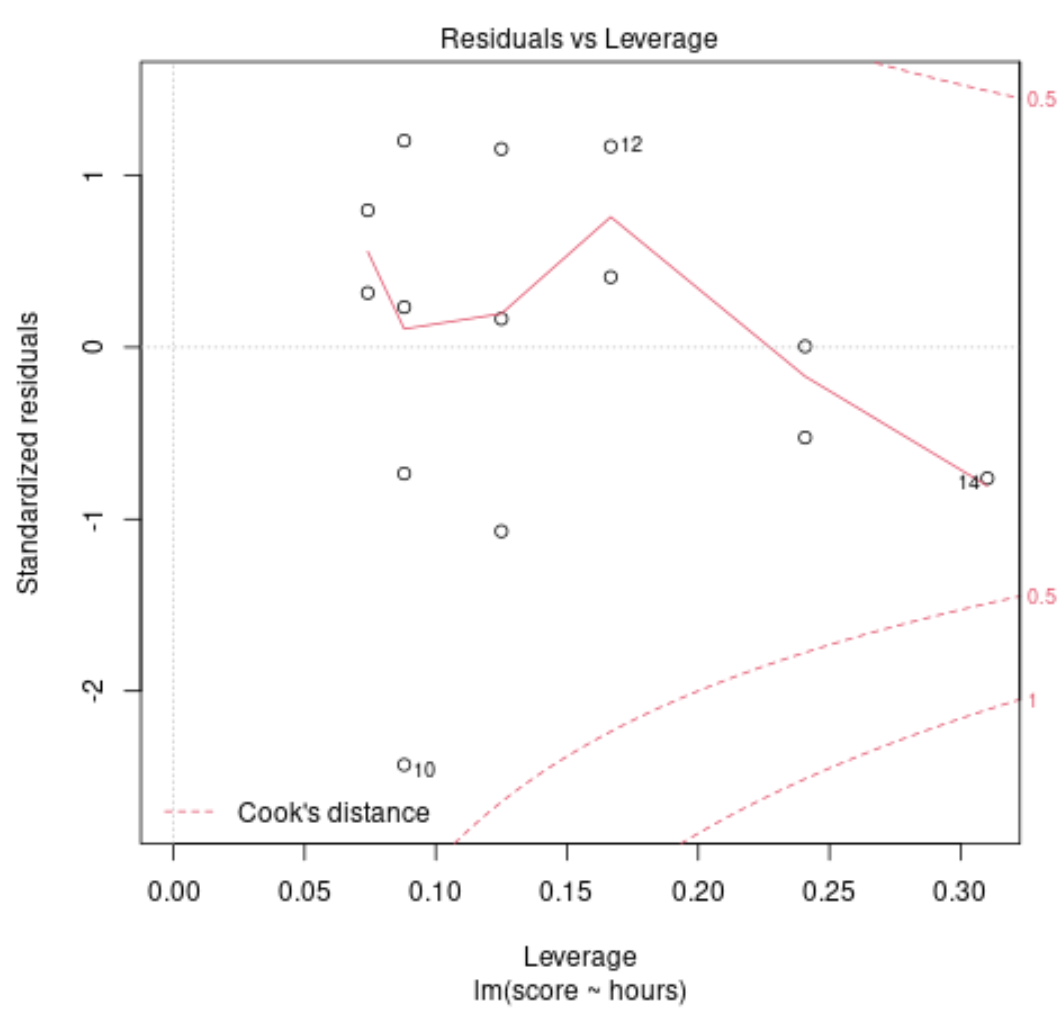
在我们的示例中,我们可以看到观测值 #10 最接近库克距离限制,但它没有落在虚线之外。这意味着我们的数据集中不存在过度影响的点。
诊断图 #2:规模和位置图
该图用于验证回归模型残差之间方差相等(也称为“同方差”)的假设。如果红线在图上近似水平,则可能满足方差相等的假设。
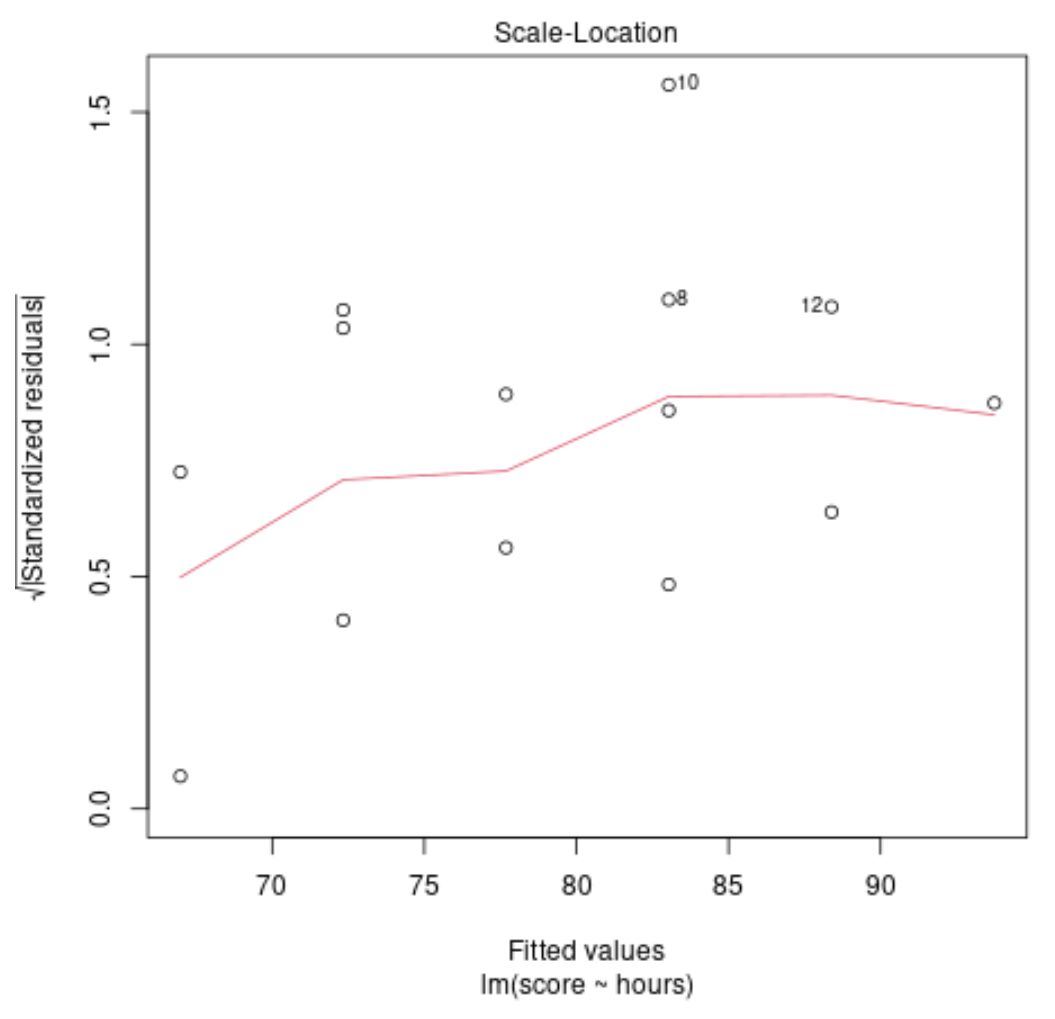
在我们的示例中,我们可以看到红线在绘图上并不完全水平,但它在任何点都不会偏离太远。我们可能会说,在这种情况下,不违反等方差的假设。
相关:了解回归分析中的异方差
诊断痕迹#3:正常的QQ痕迹
该图用于确定回归模型的残差是否呈正态分布。如果该图上的点大致沿着直线对角线分布,那么我们可以假设残差呈正态分布。
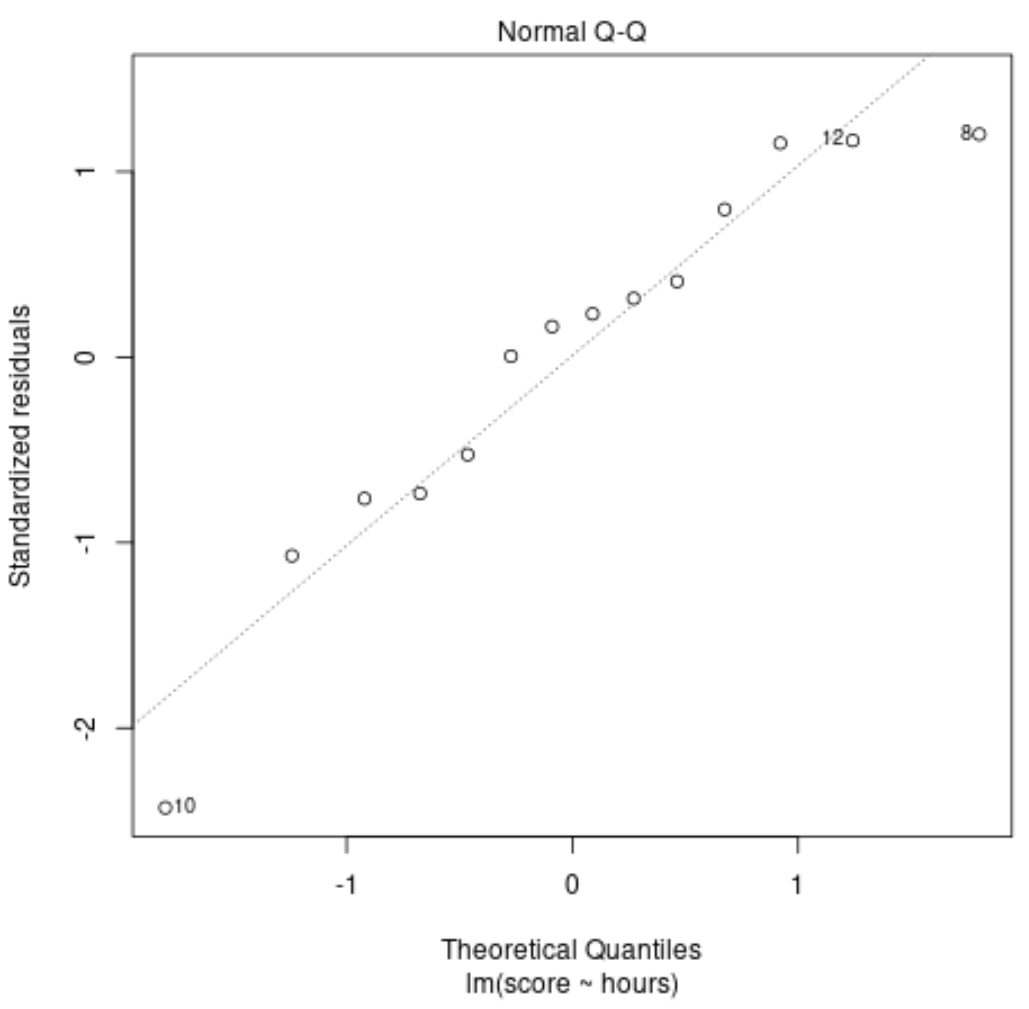
在我们的示例中,我们可以看到这些点大致沿着对角直线分布。观察值 #10 和 #8 与末端的线略有偏差,但不足以表明残差不呈正态分布。
诊断图#4:残差与残差调整后的地块
该图用于确定残差是否表现出非线性模式。如果图中心的红线近似水平,我们可以假设残差遵循线性模式。
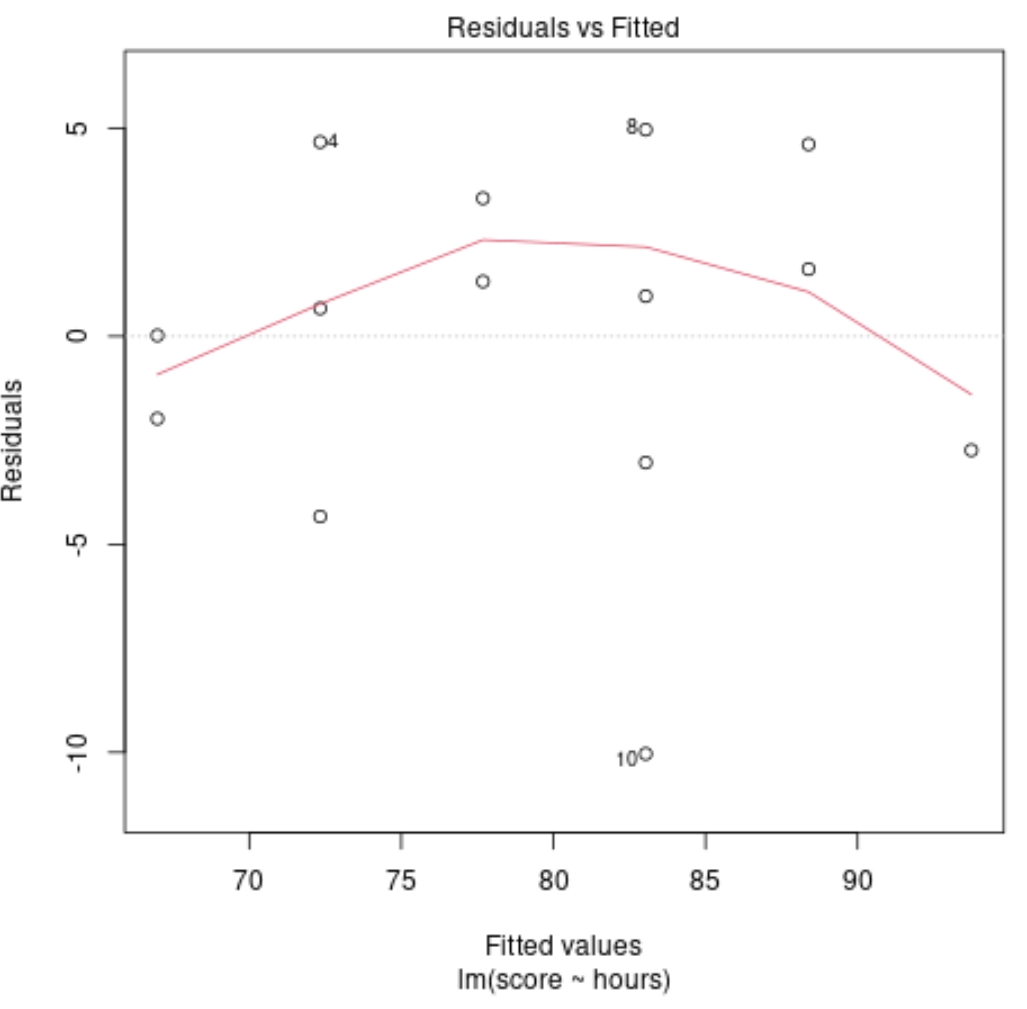
在我们的示例中,我们可以看到红线偏离了完美的水平线,但并不明显。我们可能会说残差遵循大致线性模式,并且线性回归模型适合该数据集。