如何在 r 中执行 welch t 检验

当不假设两个组具有相等方差时，韦尔奇 t 检验用于比较两个独立组之间的均值。

要在 R 中执行 Welch t 检验，我们可以使用t.test()函数，该函数使用以下语法：

t.test(x, y, Alternative = c(“两个面”, “更少”, “更大”))

金子：

• x：第一组数据值的数值向量
• y：第二组数据值的数值向量
• 替代：检验的替代假设。默认是双面的。

以下示例演示如何使用此函数在 R 中执行 Welch t 检验。

示例：R 中的 Welch t 检验

一位老师想要比较 12 名使用备考手册准备考试的学生与 12 名未使用备考手册的学生的考试结果。

以下向量显示了每组学生的考试成绩：

 booklet <- c(90, 85, 88, 89, 94, 91, 79, 83, 87, 88, 91, 90)
no_booklet <- c(67, 90, 71, 95, 88, 83, 72, 66, 75, 86, 93, 84)

在执行韦尔奇 t 检验之前，我们可以首先创建箱线图来可视化每组的分数分布：

 boxplot(booklet, no_booklet, names =c(" Booklet "," No Booklet "))

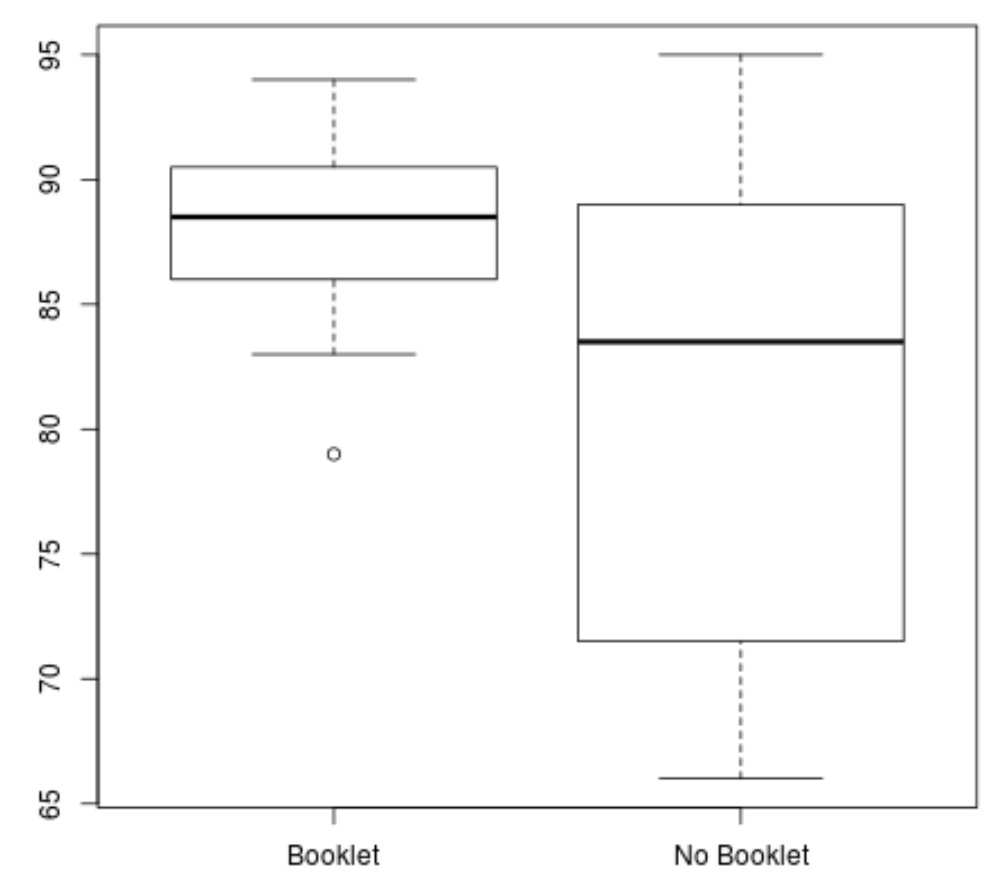
我们可以清楚地看到“Booklet”组的平均得分较高，得分方差较小。

为了正式测试各组之间的平均分数是否显着不同，我们可以执行 Welch 的 t 检验：

 #perform Welch's t-test
t.test(booklet, no_booklet)

	Welch Two Sample t-test

data: booklet and no_booklet
t = 2.2361, df = 14.354, p-value = 0.04171
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
  0.3048395 13.8618272
sample estimates:
mean of x mean of y 
 87.91667 80.83333 

从结果中，我们可以看到t检验统计量为2.2361 ，相应的 p 值为0.04171 。

由于该 p 值小于 0.05，因此我们可以拒绝零假设并得出结论：两组之间的平均考试成绩存在统计显着差异。

t.test()函数还为我们提供了以下信息：

• 两组之间平均考试成绩差异的 95%置信区间为[0.3048, 13.8618 ]。
• 第一组的平均考试成绩是87.91667 。
• 第二组的平均考试成绩是80.83333 。

您可以在此处找到 t.test() 函数的完整文档。

其他资源

以下教程解释了如何在 R 中执行其他常见任务：

如何在 R 中执行单样本 t 检验
如何在 R 中执行双样本 t 检验
如何在 R 中执行配对样本 t 检验
如何在 R 中的单个图中绘制多个箱线图