如何计算r中的马修斯相关系数

马修斯相关系数（MCC）是我们可以用来评估分类模型性能的指标。

计算方法如下：

MCC = (TP*TN – FP*FN) / √ (TP+FP)(TP+FN)(TN+FP)(TN+FN)

金子：

• TP ：真阳性数
• TN ：真阴性数
• FP ：误报数
• FN ：漏报数

当两个类不平衡时，即一个类出现的次数比另一类多得多时，该指标特别有用。

MCC 的值介于 -1 和 1 之间，其中：

• -1表示预测类别与实际类别之间完全不一致
• 0表示完全随机猜测
• 1表示预测类别与实际类别完全一致

例如，假设体育分析师使用逻辑回归模型来预测 400 名不同的大学篮球运动员是否会被选入 NBA。

以下混淆矩阵总结了模型所做的预测：

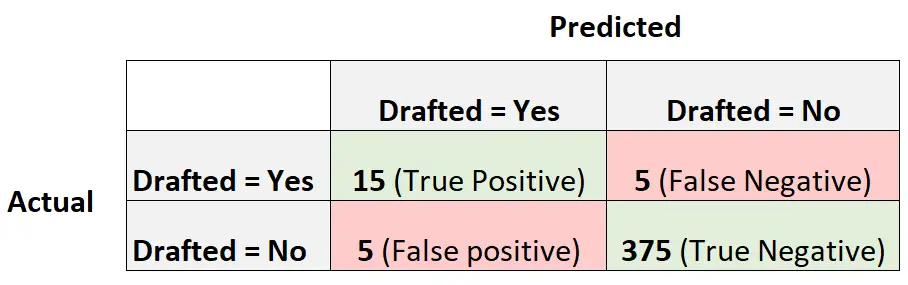
为了计算模型的MCC，我们可以使用以下公式：

• MCC = (TP*TN – FP*FN) / √ (TP+FP)(TP+FN)(TN+FP)(TN+FN)
• MCC = (15*375-5*5) / √ (15+5)(15+5)(375+5)(375+5)
• MCC = 0.7368

马修斯相关系数为0.7368 。

这个值有点接近 1，表明该模型在预测球员是否会被选中方面做得不错。

以下示例展示了如何使用 R 中mltools包中的mcc()函数计算此特定场景的 MCC。

示例：计算 R 中的马修斯相关系数

以下代码演示了如何定义预测类向量和实际类向量，然后使用mltools包中的mcc()函数计算 Matthews 相关系数：

 library (mltools)

#define vector of actual classes
actual <- rep (c(1, 0), times =c(20, 380))

#define vector of predicted classes
preds <- rep (c(1, 0, 1, 0), times =c(15, 5, 5, 375))

#calculate Matthews correlation coefficient
mcc(preds, actual)

[1] 0.7368421

马修斯相关系数为0.7368 。

这与我们之前手动计算的值相符。

如果要计算混淆矩阵的 Matthews 相关系数，可以使用fusionM参数，如下所示：

 library (mltools)

#create confusion matrix
conf_matrix <- matrix(c(15, 5, 5, 375), nrow= 2 )

#view confusion matrix
conf_matrix

     [,1] [,2]
[1,] 15 5
[2,] 5,375

#calculate Matthews correlation coefficient for confusion matrix
mcc(confusionM = conf_matrix)

[1] 0.7368421

同样，马修斯相关系数为0.7368。

其他资源

以下教程解释了如何在 R 中执行其他常见任务：

如何在 R 中执行逻辑回归
如何使用ggplot2绘制ROC曲线
如何计算R中的F1分数