如何使用r中的lm()函数来拟合线性模型

R 中的lm()函数用于拟合线性回归模型。

该函数使用以下基本语法：

lm(公式、数据、…)

金子：

• Formula：线性模型公式（例如y ~ x1 + x2）
• data：包含数据的数据块的名称

以下示例展示了如何在 R 中使用此函数来执行以下操作：

• 拟合回归模型
• 查看回归模型拟合摘要
• 查看模型诊断图
• 绘制拟合回归模型
• 使用回归模型进行预测

拟合回归模型

以下代码展示了如何使用lm()函数在 R 中拟合线性回归模型：

 #define data
df = data. frame (x=c(1, 3, 3, 4, 5, 5, 6, 8, 9, 12),
                y=c(12, 14, 14, 13, 17, 19, 22, 26, 24, 22))

#fit linear regression model using 'x' as predictor and 'y' as response variable
model <- lm(y ~ x, data=df)

显示回归模型摘要

然后我们可以使用summary()函数来显示回归模型拟合的摘要：

 #view summary of regression model
summary(model)

Call:
lm(formula = y ~ x, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4793 -0.9772 -0.4772 1.4388 4.6328 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 11.1432 1.9104 5.833 0.00039 ***
x 1.2780 0.2984 4.284 0.00267 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.929 on 8 degrees of freedom
Multiple R-squared: 0.6964, Adjusted R-squared: 0.6584 
F-statistic: 18.35 on 1 and 8 DF, p-value: 0.002675

以下是如何解释模型中最重要的值：

• F 统计量= 18.35，相应的p 值= 0.002675。由于该 p 值小于 0.05，因此整个模型具有统计显着性。
• 倍数 R 平方= 0.6964。这告诉我们，响应变量 y 中 69.64% 的变异可以由预测变量 x 来解释。
• x 的估计系数：1.2780。这告诉我们，x 每增加一个单位，y 就会平均增加 1.2780。

然后我们可以使用输出的系数估计来编写估计的回归方程：

y = 11.1432 + 1.2780*(x)

额外奖励：您可以在此处找到解释 R 中回归输出的每个值的完整指南。

查看模型诊断图

然后我们可以使用plot()函数绘制回归模型的诊断图：

 #create diagnostic plots
plot(model) 

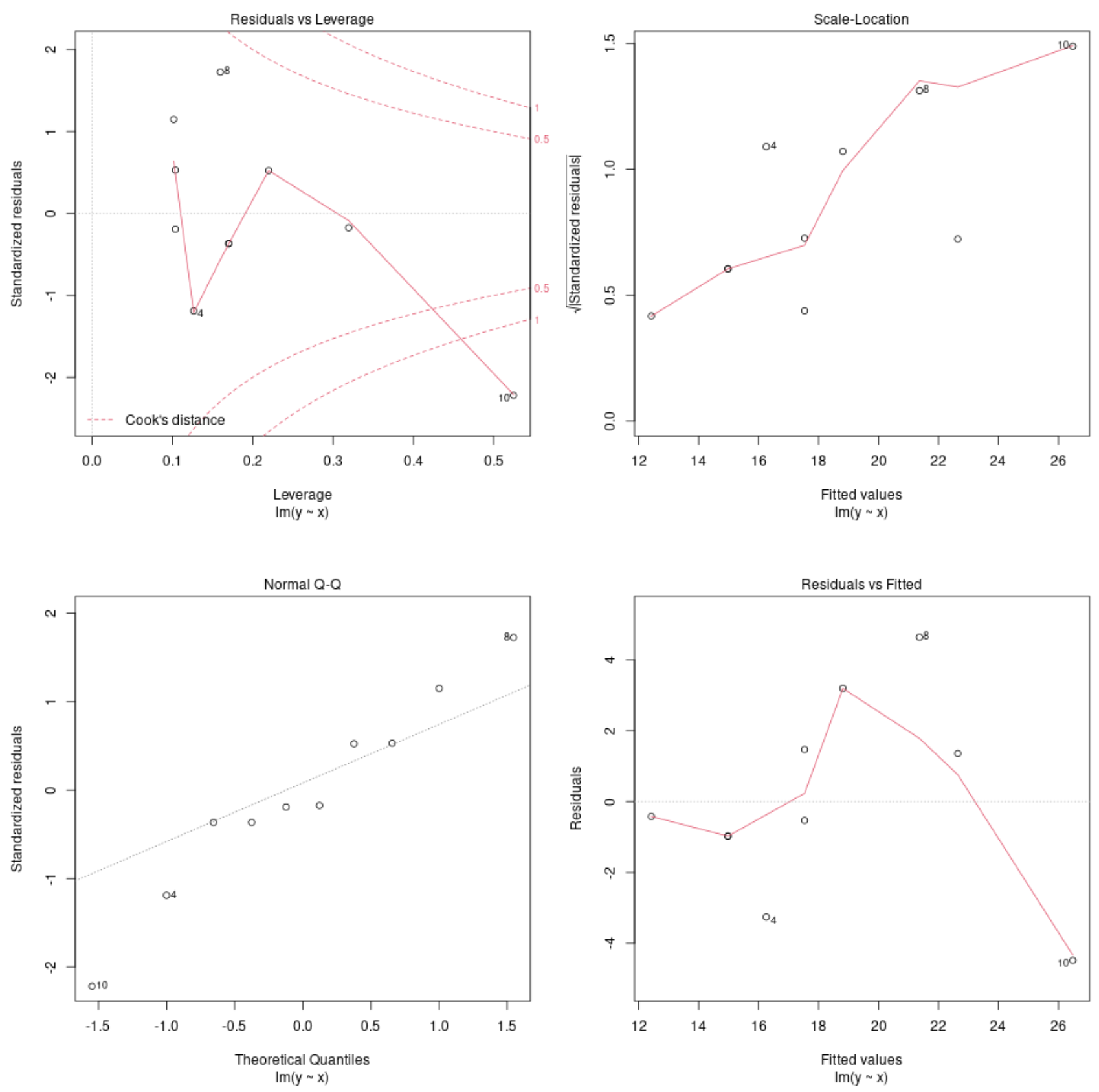
这些图表使我们能够分析回归模型的残差，以确定该模型是否适合用于数据。

请参阅本教程，了解如何在 R 中解释模型诊断图的完整说明。

绘制拟合回归模型

我们可以使用abline()函数来绘制拟合回归模型：

 #create scatterplot of raw data
plot(df$x, df$y, col=' red ', main=' Summary of Regression Model ', xlab=' x ', ylab=' y ')

#add fitted regression line
abline(model)

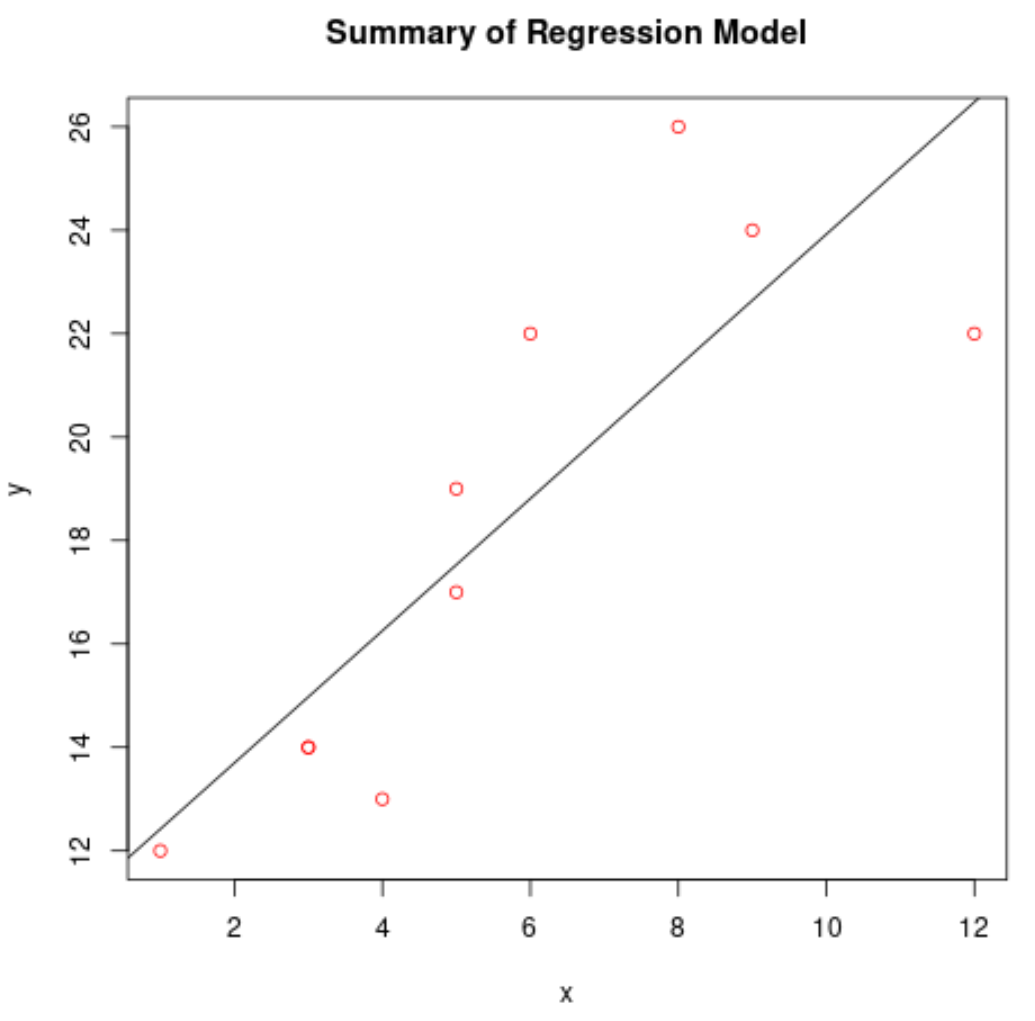
使用回归模型进行预测

我们可以使用Predict()函数来预测新观察的响应值：

 #define new observation
new <- data. frame (x=c(5))

#use the fitted model to predict the value for the new observation
predict(model, newdata = new)

      1 
17.5332

该模型预测这个新观测值的响应值为17.5332 。

其他资源

如何在 R 中执行简单线性回归
如何在 R 中执行多元线性回归
如何在 R 中执行逐步回归