R 中的主成分分析：分步示例

主成分分析（通常缩写为 PCA）是一种无监督机器学习技术，旨在找到主成分（原始预测变量的线性组合）来解释数据集中的大部分变化。

PCA 的目标是用比原始数据集更少的变量来解释数据集中的大部分变异性。

对于具有p 个变量的给定数据集，我们可以检查每个变量成对组合的散点图，但散点图的数量可能会很快变得很大。

对于p 个预测变量，存在 p(p-1)/2 个点云。

因此，对于具有 p = 15 个预测变量的数据集，将有 105 个不同的散点图！

幸运的是，PCA 提供了一种找到数据集低维表示的方法，该表示可以捕获尽可能多的数据变化。

如果我们能够捕获二维中的大部分变化，我们就可以将原始数据集中的所有观察结果投影到一个简单的散点图上。

我们找到主要组件的方式如下：

_{给定一个具有}p 个_{预测变量的数据集}： _

• _{Z m = ΣΦ jm _}
• Z ₁是预测变量的线性组合，可捕获尽可能多的方差。
• Z ₂是预测变量的下一个线性组合，它捕获最大方差，同时与 Z ₁正交（即不相关）。
• Z ₃是预测变量的下一个线性组合，它在与 Z ₂正交的同时捕获最大方差。
• 等等。

在实践中，我们使用以下步骤来计算原始预测变量的线性组合：

1.对每个变量进行缩放，使其平均值为 0，标准差为 1。

2.计算缩放变量的协方差矩阵。

3.计算协方差矩阵的特征值。

使用线性代数，我们可以证明最大特征值对应的特征向量是第一主成分。换句话说，这种特定的预测变量组合解释了数据中的最大方差。

第二大特征值对应的特征向量是第二主成分，以此类推。

本教程提供了如何在 R 中执行此过程的分步示例。

第 1 步：加载数据

我们首先加载Tidyverse包，其中包含几个用于可视化和操作数据的有用函数：

 library (tidyverse)

在本例中，我们将使用 R 中内置的USArrests数据集，其中包含 1973 年美国各州每 100,000 名居民因谋杀、袭击和强奸而被捕的人数。

它还包括每个州居住在城市地区的人口百分比UrbanPop 。

以下代码显示如何加载和显示数据集的第一行：

 #load data
data ("USArrests")

#view first six rows of data
head(USArrests)

           Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7

步骤 2：计算主成分

加载数据后，我们可以使用R的内置函数prcomp()来计算数据集的主成分。

请务必指定scale = TRUE ，以便在计算主成分之前将数据集中的每个变量缩放为平均值为0、标准差为1。

另请注意，R 中的特征向量默认指向负方向，因此我们将乘以 -1 来反转符号。

 #calculate main components
results <- prcomp(USArrests, scale = TRUE )

#reverse the signs
results$rotation <- -1*results$rotation

#display main components
results$rotation

               PC1 PC2 PC3 PC4
Murder 0.5358995 -0.4181809 0.3412327 -0.64922780
Assault 0.5831836 -0.1879856 0.2681484 0.74340748
UrbanPop 0.2781909 0.8728062 0.3780158 -0.13387773
Rape 0.5434321 0.1673186 -0.8177779 -0.08902432

我们可以看到，第一主成分（PC1）对于谋杀、袭击和强奸具有很高的值，表明该主成分描述了这些变量中最大的变异。

我们还可以看到，第二主成分（PC2）对于 UrbanPop 具有较高的值，表明该主成分强调城市人口。

请注意，每个州的主成分分数存储在results$x中。我们还将这些分数乘以 -1 以反转符号：

 #reverse the signs of the scores
results$x <- -1*results$x

#display the first six scores
head(results$x)

                  PC1 PC2 PC3 PC4
Alabama 0.9756604 -1.1220012 0.43980366 -0.154696581
Alaska 1.9305379 -1.0624269 -2.01950027 0.434175454
Arizona 1.7454429 0.7384595 -0.05423025 0.826264240
Arkansas -0.1399989 -1.1085423 -0.11342217 0.180973554
California 2.4986128 1.5274267 -0.59254100 0.338559240
Colorado 1.4993407 0.9776297 -1.08400162 -0.001450164

第 3 步：使用双图可视化结果

接下来，我们可以创建一个双图——将数据集中的每个观测值投影到使用第一和第二主成分作为轴的散点图上的图：

请注意， scale = 0确保图中的箭头按比例缩放以表示载荷。

 biplot(results, scale = 0 )

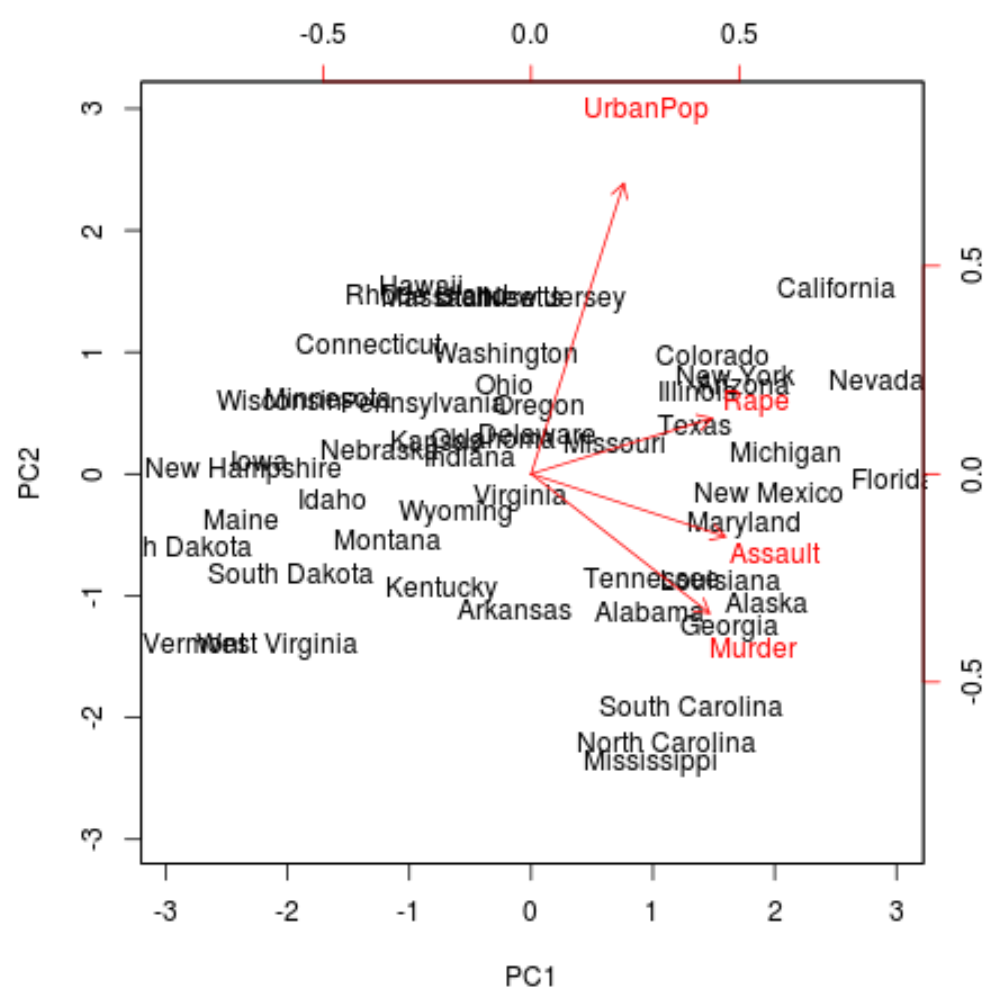
从图中我们可以看到 50 个状态中的每一个都在一个简单的二维空间中表示。

图表上彼此接近的状态对于原始数据集中的变量具有相似的数据模式。

我们还可以看到，一些州与某些犯罪的关联性比其他州更强烈。例如，佐治亚州是图中最接近谋杀变量的州。

如果我们查看原始数据集中谋杀率最高的州，我们可以看到佐治亚州实际上位居榜首：

 #display states with highest murder rates in original dataset
head(USArrests[ order (-USArrests$Murder),])

               Murder Assault UrbanPop Rape
Georgia 17.4 211 60 25.8
Mississippi 16.1 259 44 17.1
Florida 15.4 335 80 31.9
Louisiana 15.4 249 66 22.2
South Carolina 14.4 279 48 22.5
Alabama 13.2 236 58 21.2

步骤 4：找出每个主成分解释的方差

我们可以使用以下代码来计算每个主成分解释的原始数据集中的总方差：

 #calculate total variance explained by each principal component
results$sdev^2 / sum (results$sdev^2)

[1] 0.62006039 0.24744129 0.08914080 0.04335752

从结果中，我们可以观察到以下几点：

• 第一个主成分解释了数据集中总方差的62% 。
• 第二个主成分解释了数据集中总方差的24.7% 。
• 第三主成分解释了数据集中总方差的8.9% 。
• 第四个主成分解释了数据集中总方差的4.3% 。

因此，前两个主成分解释了数据中总方差的大部分。

这是一个好兆头，因为之前的双图将原始数据中的每个观测值投影到仅考虑前两个主成分的散点图上。

因此，检查双图中的模式以识别彼此相似的状态是有效的。

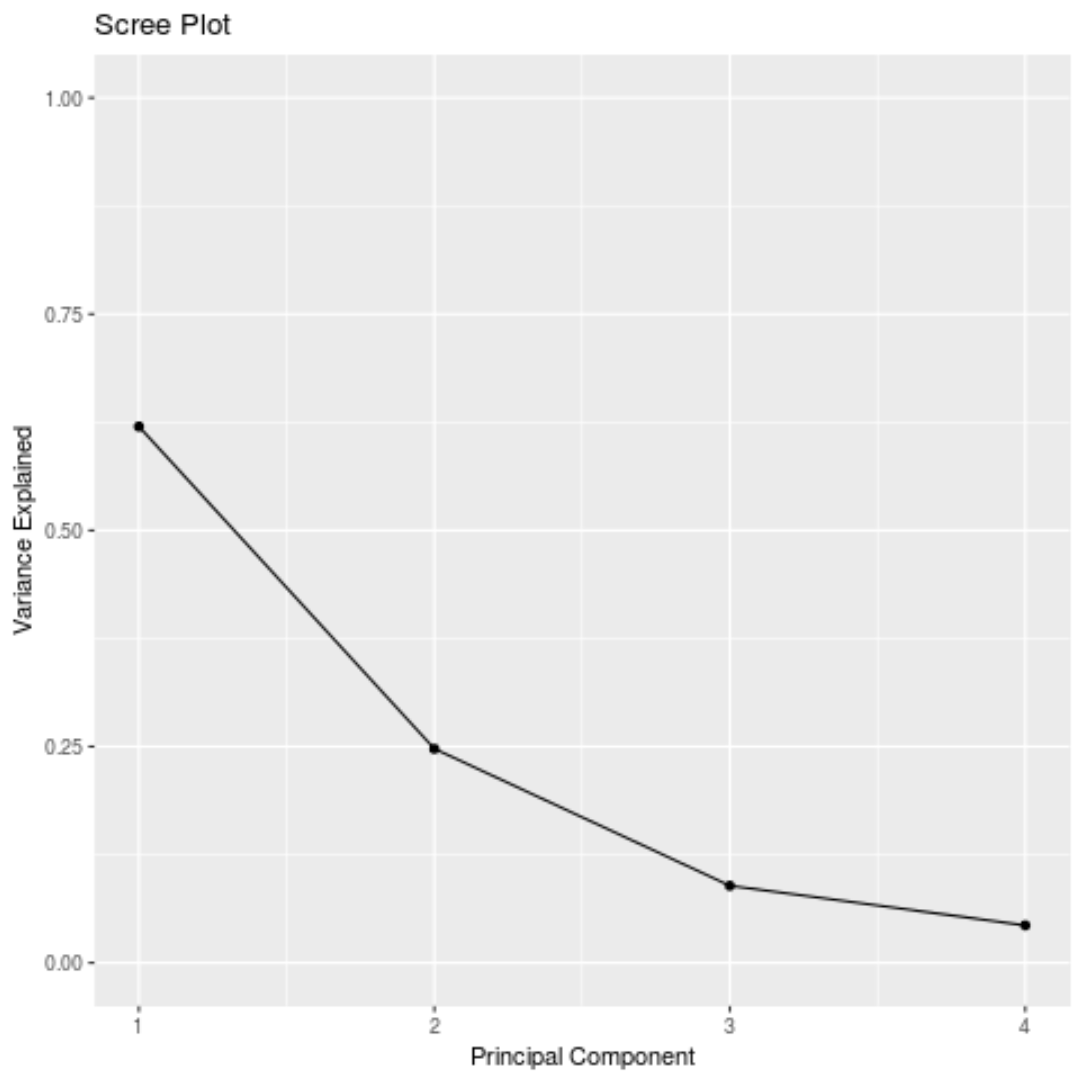
我们还可以创建一个碎石图——显示每个主成分解释的总方差的图表——以可视化 PCA 结果：

 #calculate total variance explained by each principal component
var_explained = results$sdev^2 / sum (results$sdev^2)

#create scree plot
qplot(c(1:4), var_explained) + 
  geom_line() + 
  xlab(" Principal Component ") + 
  ylab(" Variance Explained ") +
  ggtitle(" Scree Plot ") +
  ylim(0, 1) 

主成分分析实践

在实践中，PCA 最常用的原因有两个：

1. 探索性数据分析– 当我们第一次探索数据集并想要了解数据中的哪些观察结果彼此最相似时，我们会使用 PCA。

2. 主成分回归——我们还可以使用PCA计算主成分，然后将其用于主成分回归。当数据集中的预测变量之间存在多重共线性时，通常会使用这种类型的回归。

本教程中使用的完整 R 代码可以在此处找到。