如何在 r 中执行双变量分析(附示例)
术语双变量分析是指对两个变量的分析。你可以记住这一点,因为前缀“bi”的意思是“二”。
双变量分析的目标是了解两个变量之间的关系
执行双变量分析的常用方法有以下三种:
1.点云
2.相关系数
3.简单线性回归
以下示例演示如何使用以下包含两个变量信息的数据集执行每种类型的双变量分析: (1)学习时间和(2) 20 名不同学生获得的测试成绩:
#create data frame df <- data. frame (hours=c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 5, 5, 6, 6, 6, 7, 8), score=c(75, 66, 68, 74, 78, 72, 85, 82, 90, 82, 80, 88, 85, 90, 92, 94, 94, 88, 91, 96)) #view first six rows of data frame head(df) hours score 1 1 75 2 1 66 3 1 68 4 2 74 5 2 78 6 2 72
1. 点云
我们可以使用以下语法在 R 中创建学习时间与考试成绩的散点图:
#create scatterplot of hours studied vs. exam score plot(df$hours, df$score, pch= 16 , col=' steelblue ', main=' Hours Studied vs. Exam Score ', xlab=' Hours Studied ', ylab=' Exam Score ')
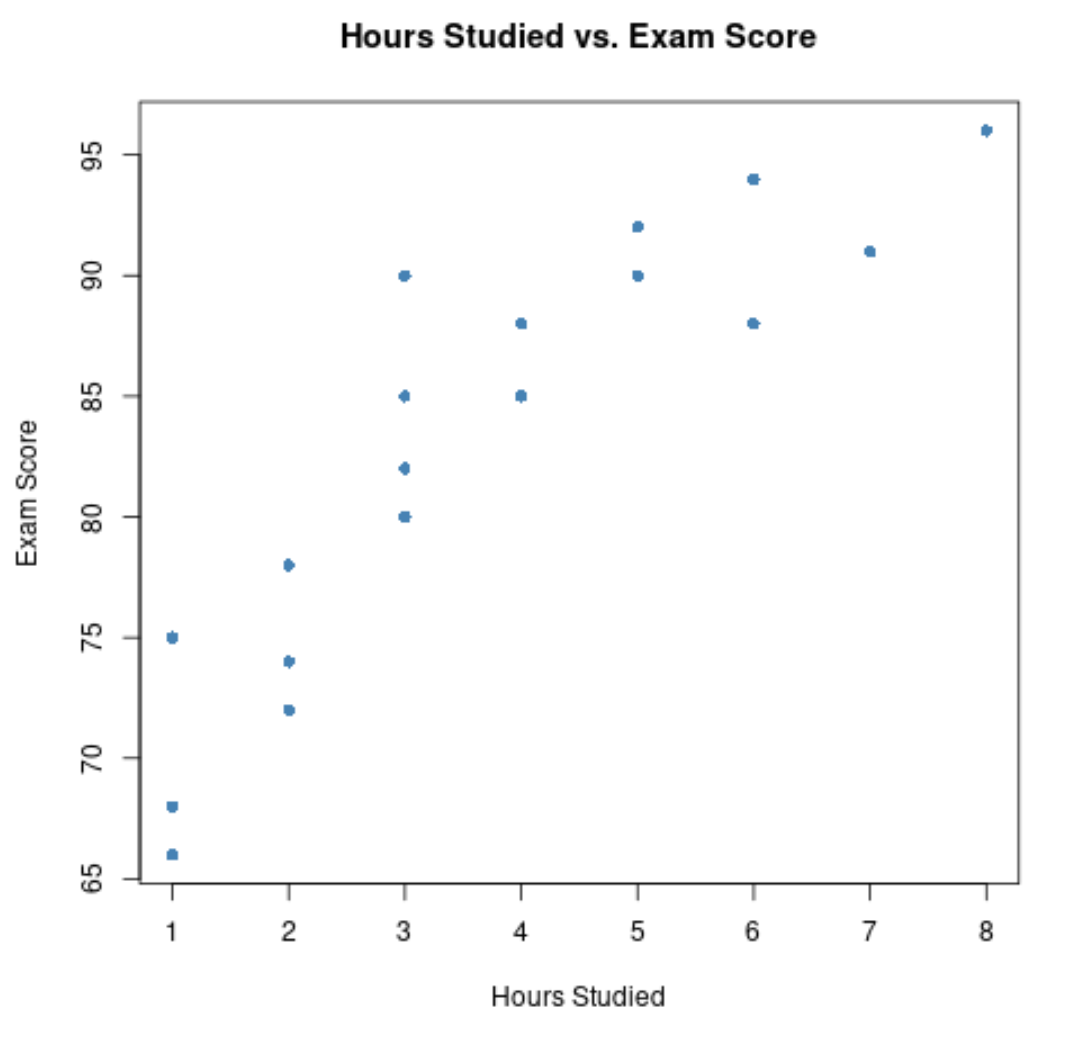
x 轴显示学习时间,y 轴显示考试成绩。
该图显示,两个变量之间存在正相关关系:随着学习时数的增加,考试成绩也趋于增加。
2. 相关系数
皮尔逊相关系数是一种量化两个变量之间线性关系的方法。
我们可以使用R中的cor()函数来计算两个变量之间的皮尔逊相关系数:
#calculate correlation between hours studied and exam score received
cor(df$hours, df$score)
[1] 0.891306
相关系数为0.891 。
该值接近 1,表明学习时间和考试成绩之间存在很强的正相关关系。
3. 简单线性回归
简单线性回归是一种统计方法,我们可以用它来找到最“适合”一组数据的直线方程,然后我们可以用它来理解两个变量之间的确切关系。
我们可以使用 R 中的lm()函数来拟合学习时间和收到的考试结果的简单线性回归模型:
#fit simple linear regression model fit <- lm(score ~ hours, data=df) #view summary of model summary(fit) Call: lm(formula = score ~ hours, data = df) Residuals: Min 1Q Median 3Q Max -6,920 -3,927 1,309 1,903 9,385 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 69.0734 1.9651 35.15 < 2nd-16 *** hours 3.8471 0.4613 8.34 1.35e-07 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 4.171 on 18 degrees of freedom Multiple R-squared: 0.7944, Adjusted R-squared: 0.783 F-statistic: 69.56 on 1 and 18 DF, p-value: 1.347e-07
拟合后的回归方程为:
考试成绩 = 69.0734 + 3.8471*(学习时间)
这告诉我们,每多学习一小时,考试成绩就会平均提高3.8471 。
我们还可以使用拟合回归方程根据学习的总小时数来预测学生将获得的分数。
例如,学习 3 小时的学生应该得到81.6147的分数:
- 考试成绩 = 69.0734 + 3.8471*(学习时间)
- 考试成绩 = 69.0734 + 3.8471*(3)
- 考试成绩 = 81.6147
其他资源
以下教程提供有关双变量分析的其他信息: