R 中的多元自适应回归样条

多元自适应回归样条(MARS) 可用于对一组预测变量和响应变量之间的非线性关系进行建模。

该方法的工作原理如下：

1.将数据集分为k块。

2.对每个部分拟合回归模型。

3.使用 k 折交叉验证来选择k的值。

本教程提供了如何将 MARS 模型拟合到 R 数据集的分步示例。

第1步：加载必要的包

在本示例中，我们将使用 ISLR工资数据集。  数据包，其中包含 3,000 人的年薪以及各种预测变量，例如年龄、教育程度、种族等。

在将 MARS 模型拟合到数据之前，我们将加载必要的包：

 library (ISLR) #contains Wage dataset
library (dplyr) #data wrangling
library (ggplot2) #plotting
library (earth) #fitting MARS models
library (caret) #tuning model parameters

第2步：查看数据

接下来，我们将显示我们正在使用的数据集的前六行：

 #view first six rows of data
head (Wage)

       year age maritl race education region
231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic
86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic
161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic
155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic
11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic
376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic
             jobclass health health_ins logwage wage
231655 1. Industrial 1. <=Good 2. No 4.318063 75.04315
86582 2. Information 2. >=Very Good 2. No 4.255273 70.47602
161300 1. Industrial 1. <=Good 1. Yes 4.875061 130.98218
155159 2. Information 2. >=Very Good 1. Yes 5.041393 154.68529
11443 2. Information 1. <=Good 1. Yes 4.318063 75.04315
376662 2. Information 2. >=Very Good 1. Yes 4.845098 127.11574

步骤 3：创建并优化 MARS 模型

接下来，我们将为该数据集创建 MARS 模型，并执行k 倍交叉验证，以确定哪个模型产生最低的测试 RMSE（均方误差）。

 #create a tuning grid
hyper_grid <- expand. grid (degree = 1:3,
                          nprune = seq (2, 50, length.out = 10) %>%
floor ())

#make this example reproducible
set.seed(1)

#fit MARS model using k-fold cross-validation
cv_mars <- train(
  x = subset(Wage, select = -c(wage, logwage)),
  y = Wage$wage,
  method = " earth ",
  metric = " RMSE ",
  trControl = trainControl(method = " cv ", number = 10),
  tuneGrid = hyper_grid)

#display model with lowest test RMSE
cv_mars$results %>%
  filter (nprune==cv_mars$bestTune$nprune, degree =cv_mars$bestTune$degree)    
degree nprune RMSE Rsquared MAE RMSESD RsquaredSD MAESD		
1 12 33.8164 0.3431804 22.97108 2.240394 0.03064269 1.4554

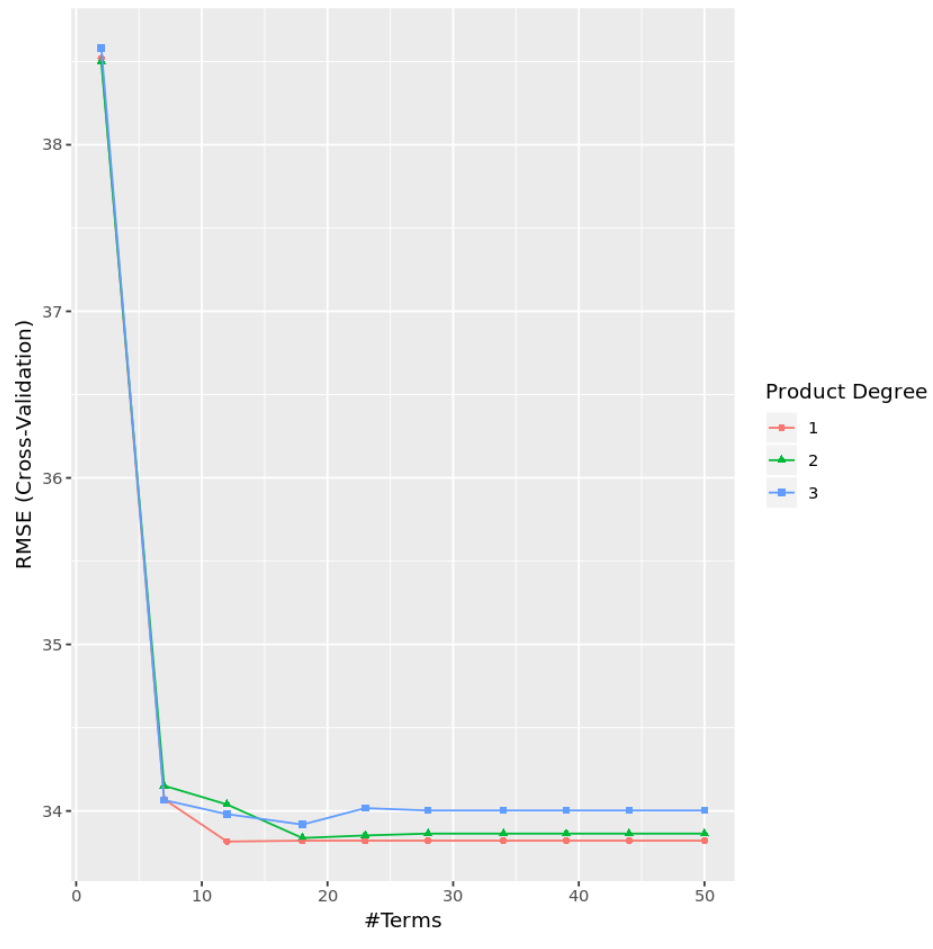
从结果中，我们可以看到，产生最低测试 MSE 的模型是仅具有一阶效应（即没有交互项）和 12 项的模型。该模型产生的均方根误差 (RMSE) 为33.8164 。

注意：我们使用 method=”earth” 来指定 MARS 模型。您可以在此处找到此方法的文档。

我们还可以创建一个图表，根据度数和项数来可视化 RMSE 测试：

 #display test RMSE by terms and degree
ggplot(cv_mars)

在实践中，我们会将 MARS 模型与其他几种类型的模型相适应，例如：

• 多元线性回归
• 多项式回归
• 峰值回归
• 套索回归
• 主成分回归
• 偏最小二乘法

然后，我们将比较每个模型，以确定哪个模型导致测试误差最低，并选择该模型作为要使用的最佳模型。

此示例中使用的完整 R 代码可以在此处找到。