如何在 r 中执行失拟检验（逐步）

失拟检验用于确定完整回归模型是否比模型的简化版本更适合数据集。

例如，假设我们想要使用学习小时数来预测某所大学学生的考试成绩。我们可以决定采用以下两个回归模型：

完整模型：分数 = β ₀ + B ₁ （小时）+ B ₂ （小时） ²

简化模型：分数 = β ₀ + B ₁ （小时）

以下分步示例展示了如何在 R 中执行失拟检验，以确定完整模型是否提供比简化模型明显更好的拟合。

步骤 1：创建并可视化数据集

首先，我们将使用以下代码创建一个数据集，其中包含 50 名学生的学习小时数和考试成绩：

 #make this example reproducible
set. seeds (1)

#create dataset
df <- data. frame (hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(df)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

接下来，我们将创建一个散点图来可视化小时数和分数之间的关系：

 #load ggplot2 visualization package
library (ggplot2)

#create scatterplot
ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

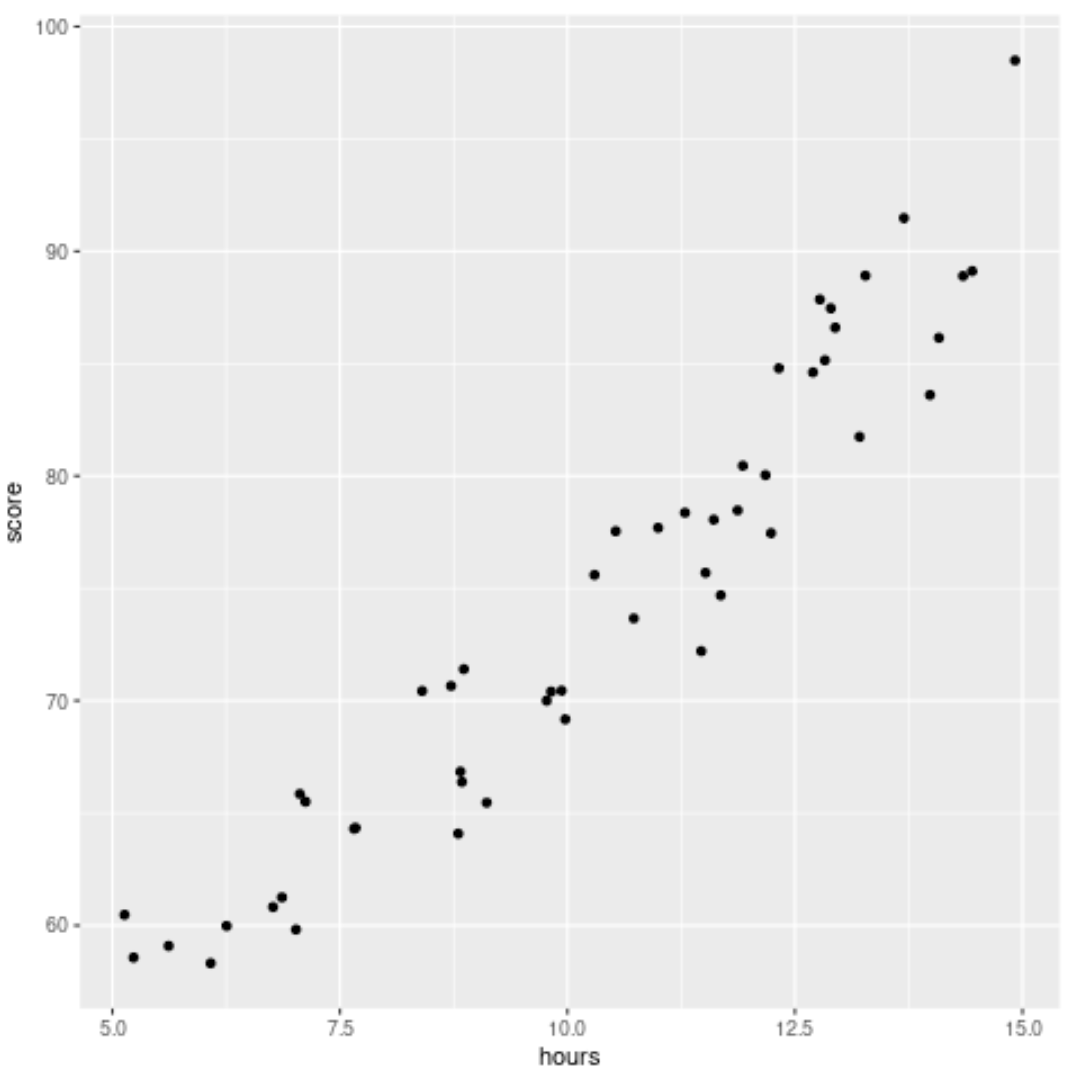
第 2 步：将两个不同的模型拟合到数据集

接下来，我们将两个不同的回归模型拟合到数据集：

 #fit full model
full <- lm(score ~ poly (hours,2), data=df)

#fit reduced model
reduced <- lm(score ~ hours, data=df)

第 3 步：执行失密检验

接下来，我们将使用anova()命令在两个模型之间执行失拟检验：

 #lack of fit test
anova(full, reduced)

Analysis of Variance Table

Model 1: score ~ poly(hours, 2)
Model 2: score ~ hours
  Res.Df RSS Df Sum of Sq F Pr(>F)   
1 47 368.48                                
2 48 451.22 -1 -82.744 10.554 0.002144 **
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

F 检验统计量结果为10.554 ，相应的 p 值为0.002144 。由于该 p 值小于 0.05，因此我们可以拒绝检验的原假设，并得出结论：完整模型在统计上比简化模型提供了显着更好的拟合。

第 4 步：可视化最终模型

最后，我们可以根据原始数据集可视化最终模型（完整模型）：

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

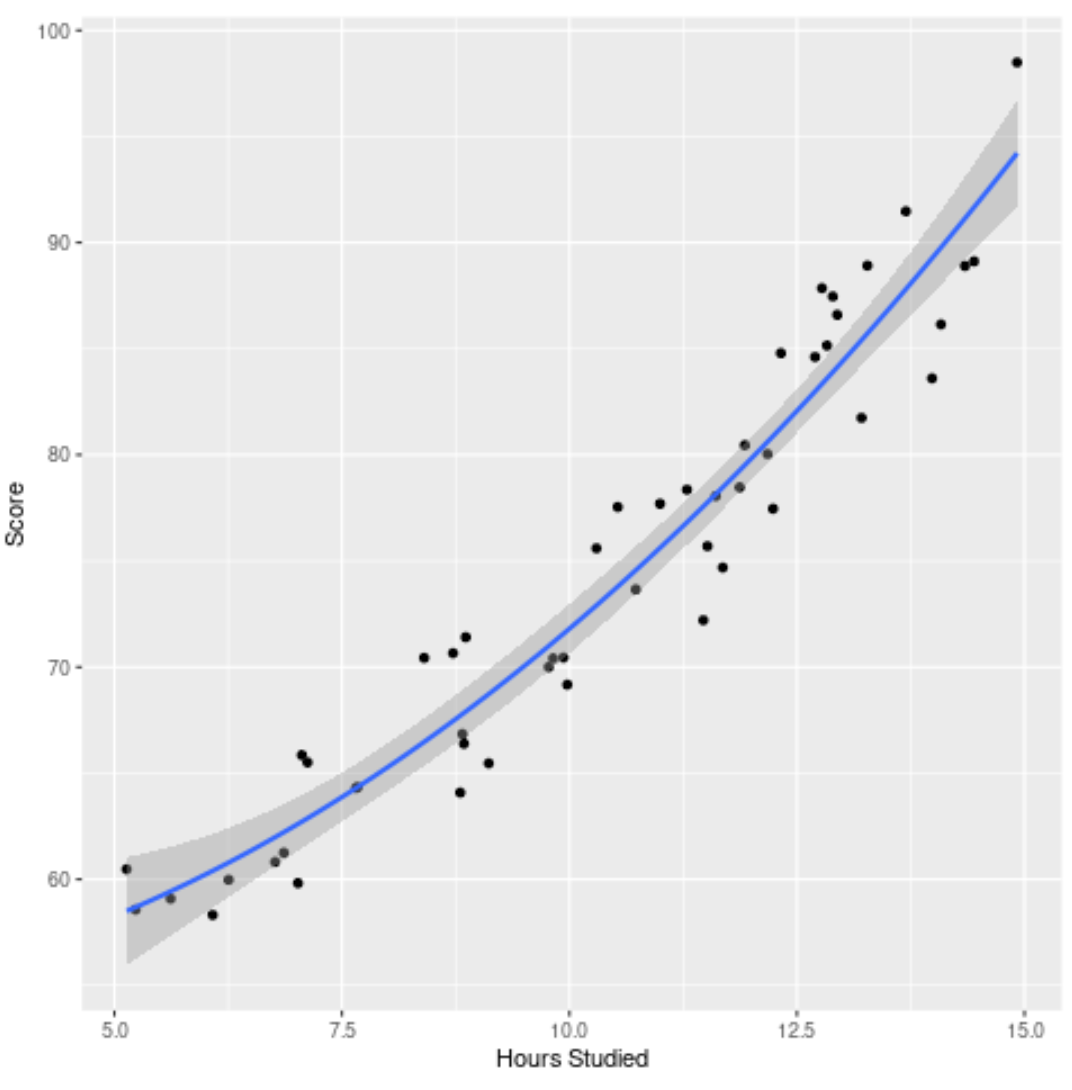
我们可以看到模型曲线与数据拟合得很好。

其他资源

如何在 R 中执行简单线性回归
如何在 R 中执行多元线性回归
如何在 R 中执行多项式回归