R 中的套索回归(一步一步)
当数据中存在多重共线性时,套索回归是一种可以用来拟合回归模型的方法。
简而言之,最小二乘回归试图找到最小化残差平方和 (RSS) 的系数估计:
RSS = Σ(y i – ŷ i )2
金子:
- Σ :希腊符号,意思是和
- y i :第 i 个观测值的实际响应值
- ŷ i :基于多元线性回归模型的预测响应值
相反,套索回归旨在最小化以下因素:
RSS + λΣ|β j |
其中j从 1 到p 个预测变量且 λ ≥ 0。
等式中的第二项称为提款罚金。在套索回归中,我们选择产生尽可能最低的 MSE(均方误差)测试的 λ 值。
本教程提供了如何在 R 中执行套索回归的分步示例。
第 1 步:加载数据
对于此示例,我们将使用 R 的内置数据集mtcars 。我们将使用hp作为响应变量,并使用以下变量作为预测变量:
- 英里/加仑
- 重量
- 拉屎
- 快秒
为了执行套索回归,我们将使用glmnet包中的函数。该包要求响应变量是一个向量,并且预测变量集是data.matrix类。
下面的代码展示了如何定义我们的数据:
#define response variable
y <- mtcars$hp
#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])
步骤 2:拟合套索回归模型
接下来,我们将使用glmnet()函数来拟合 lasso 回归模型并指定alpha=1 。
请注意,将 alpha 设置为 0 相当于使用 岭回归,将 alpha 设置为 0 到 1 之间的值相当于使用弹性网络。
为了确定 lambda 使用哪个值,我们将执行k 倍交叉验证并确定产生最低测试均方误差 (MSE) 的 lambda 值。
请注意, cv.glmnet()函数使用 k = 10 次自动执行 k 倍交叉验证。
library (glmnet)
#perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 1 )
#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda
[1] 5.616345
#produce plot of test MSE by lambda value
plot(cv_model)
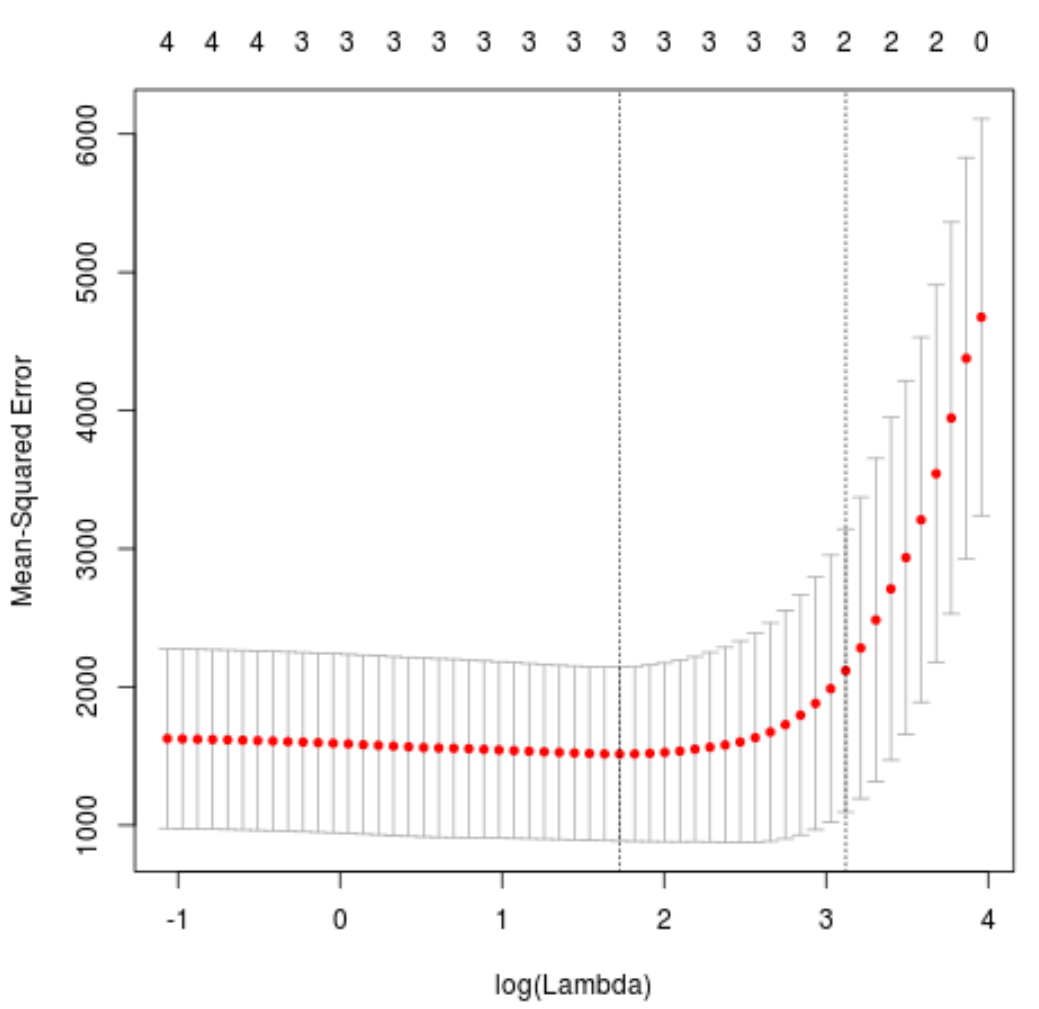
最小化 MSE 测试的 lambda 值是5.616345 。
第 3 步:分析最终模型
最后,我们可以分析最优 lambda 值产生的最终模型。
我们可以使用以下代码来获得该模型的系数估计:
#find coefficients of best model
best_model <- glmnet(x, y, alpha = 1 , lambda = best_lambda)
coef(best_model)
5 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) 484.20742
mpg -2.95796
wt 21.37988
drat.
qsec -19.43425
没有显示drat预测器的系数,因为套索回归将系数降低到零。这意味着他因为没有足够的影响力而被彻底从模特中剔除。
请注意,这是岭回归和套索回归之间的主要区别。岭回归将所有系数减少到零,但套索回归有可能通过将系数完全减少到零来从模型中删除预测变量。
我们还可以使用最终的套索回归模型来对新的观察结果进行预测。例如,假设我们有一辆具有以下属性的新车:
- 英里/加仑:24
- 重量:2.5
- 价格:3.5
- 秒:18.5
以下代码展示了如何使用拟合的套索回归模型来预测这个新观测值的hp值:
#define new observation
new = matrix(c(24, 2.5, 3.5, 18.5), nrow= 1 , ncol= 4 )
#use lasso regression model to predict response value
predict(best_model, s = best_lambda, newx = new)
[1,] 109.0842
根据输入的值,模型预测这辆车的马力值为109.0842 。
最后,我们可以在训练数据上计算模型的 R 平方:
#use fitted best model to make predictions
y_predicted <- predict (best_model, s = best_lambda, newx = x)
#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)
#find R-Squared
rsq <- 1 - sse/sst
rsq
[1] 0.8047064
R 平方结果为0.8047064 。也就是说,最好的模型能够解释训练数据响应值的80.47%的变异。
您可以在此处找到本示例中使用的完整 R 代码。