如何在 sas 中执行主成分分析

主成分分析 (PCA) 是一种 无监督机器学习技术，旨在寻找主成分（预测变量的线性组合）来解释数据集中的大部分变化。

在 SAS 中执行 PCA 最简单的方法是使用PROC PRINCOMP语句，该语句使用以下基本语法：

 proc princomp data =my_data out =out_data outstat =stats;
    var var1 var2 var3;
run ;

以下是每条指令的作用：

• data ：用于 PCA 的数据集的名称
• out ：要创建的数据集的名称，其中包含所有原始数据加上主成分分数
• outstat ：指定应创建包含均值、标准差、相关系数、特征值和特征向量的数据集。
• var ：输入数据集中用于 PCA 的变量。

以下分步示例展示了如何在实践中使用PROC PRINCOMP语句在 SAS 中执行主成分分析。

第 1 步：创建数据集

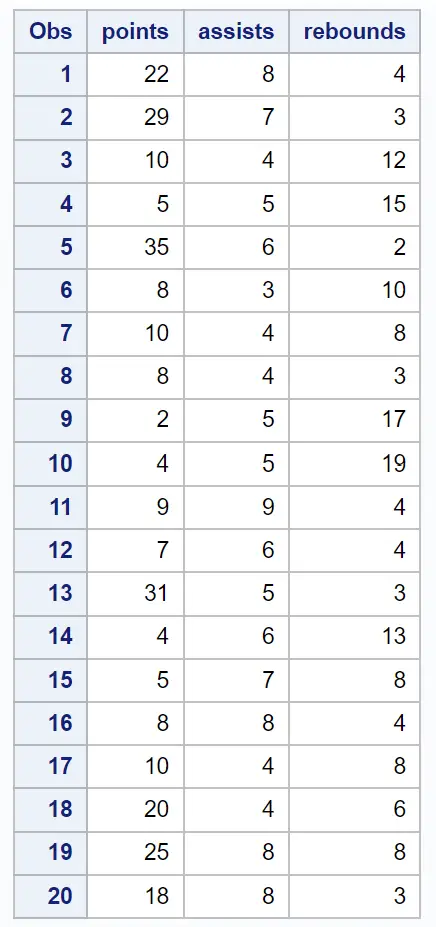
假设我们有以下数据集，其中包含 20 名篮球运动员的各种信息：

 /*create dataset*/
data my_data;
    input points assists rebounds;
    datalines ;
22 8 4
29 7 3
10 4 12
5 5 15
35 6 2
8 3 10
10 4 8
8 4 3
2 5 17
4 5 19
9 9 4
7 6 4
31 5 3
4 6 13
5 7 8
8 8 4
10 4 8
20 4 6
25 8 8
18 8 3
;
run ;

/*view dataset*/
proc print data =my_data; 

步骤 2：执行主成分分析

我们可以使用PROC PRINCOMP语句使用数据集的point 、 Assists和ounces变量来执行主成分分析：

 /*perform principal components analysis*/
proc princomp data =my_data out =out_data outstat =stats;
    var points assists rebounds;
run ;

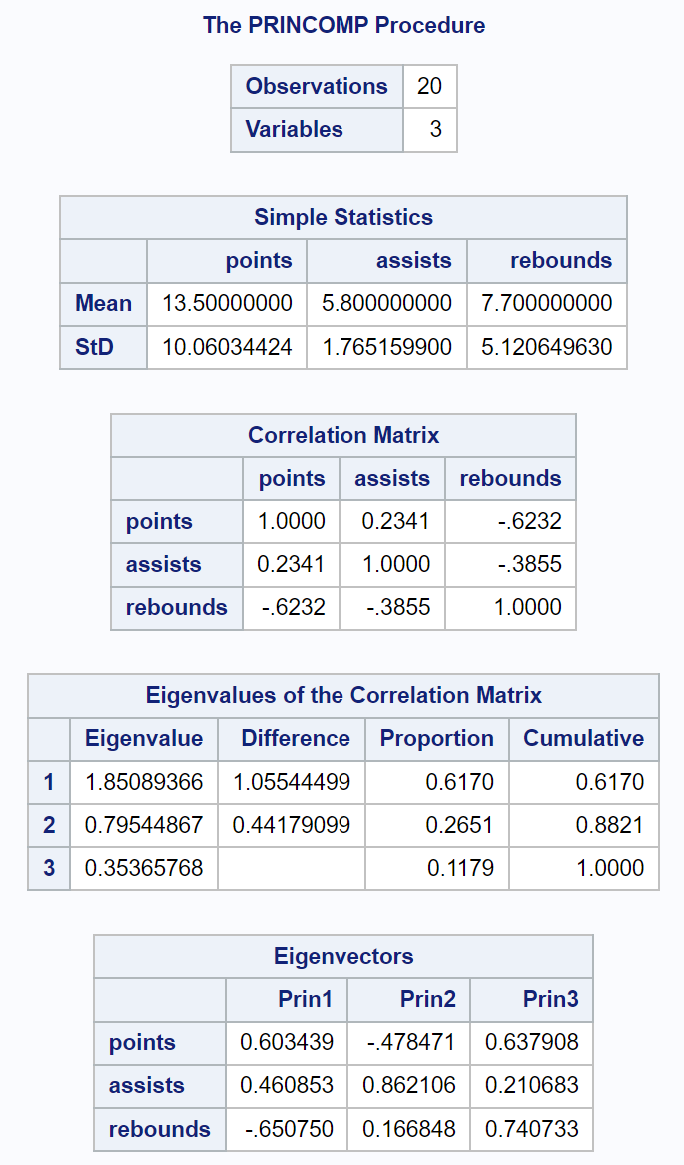
输出的第一部分显示各种描述性统计数据，包括每个输入变量的平均值和标准差、相关矩阵以及特征值和特征向量的值：

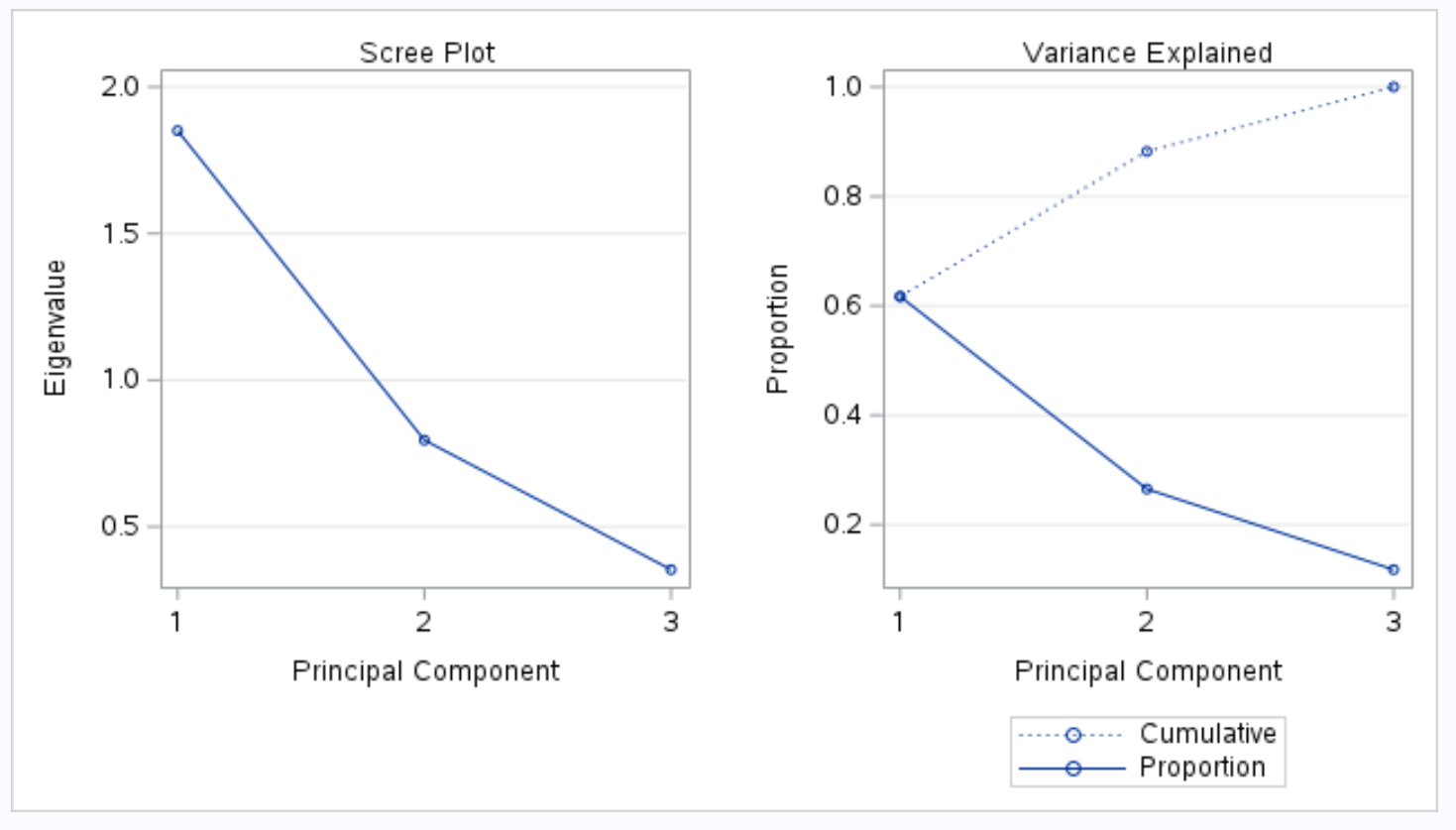
输出的下一部分显示碎石图和解释方差图：

当我们执行 PCA 时，我们经常想要了解每个主成分可以解释数据集中总变异的百分比。

标题为“相关矩阵特征值”的结果表使我们能够准确地看到每个主成分解释了总变异的百分比：

• 第一个主成分解释了数据集中总变异的61.7% 。
• 第二个主成分解释了数据集中总变异的26.51% 。
• 第三主成分解释了数据集中总变异的11.79% 。

请注意，所有百分比加起来为 100%。

然后，标题为“方差解释”的图允许我们可视化这些值。

x 轴显示主成分，y 轴显示每个主成分解释的总方差的百分比。

步骤 3：创建双图来可视化结果

为了可视化给定数据集的 PCA 结果，我们可以创建一个双标图，它是在由前两个主成分形成的平面上显示数据集中的每个观测值的图。

我们可以在 SAS 中使用以下语法来创建双图：

 /*create dataset with column called obs to represent row numbers of original data*/
data biplot_data;
   set out_data;
   obs=_n_;
run ;

/*create biplot using values from first two principal components*/
proc sgplot data =biplot_data;
    scatter x =Prin1 y =Prin2 / datalabel =obs;
run ; 

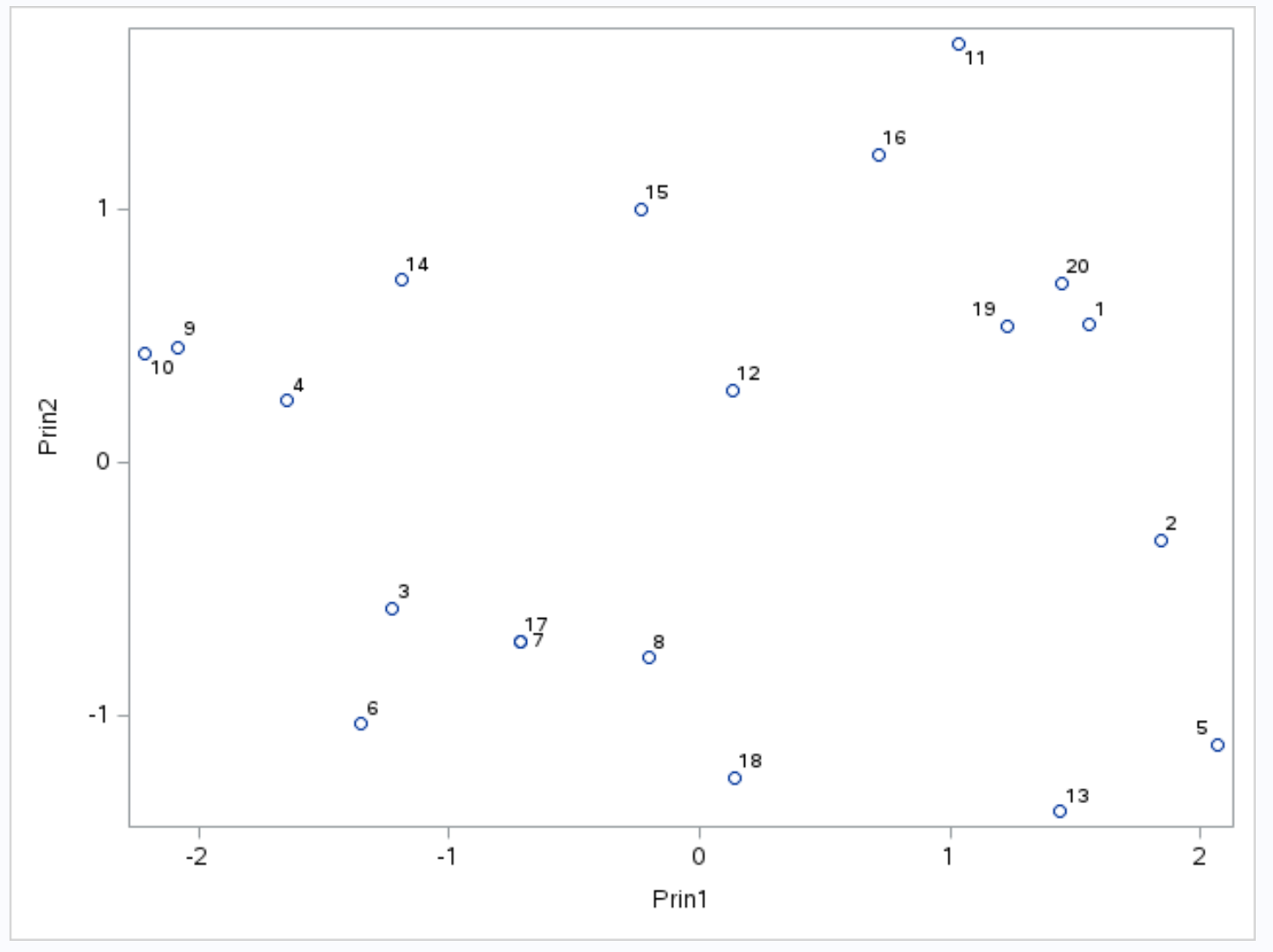
x 轴显示第一主成分，y 轴显示第二主成分，数据集中的各个观测值在图形内显示为小圆圈。

图表上并排的观察结果对于得分、助攻和篮板这三个变量具有相似的值。

例如，在图的最左侧，我们可以看到观测值#9和#10彼此非常接近。

如果我们参考原始数据集，我们可以看到这些观察结果的以下值：

• 观察 n°9 ：2 分、5 次助攻、17 个篮板
• 观察#10 ：4分、5次助攻、19个篮板

三个变量中每个变量的值都相似，这解释了为什么这些观察结果在双图上彼此如此接近。

我们还在标题为Correlation Matrix Eigenvalues 的结果表中看到，前两个主成分占数据集中总变异的88.21% 。

由于这个百分比非常高，因此分析双图中的哪些观测值彼此接近是有效的，因为组成双图的两个主要成分几乎解释了数据集中的所有变化。

其他资源

以下教程解释了如何在 SAS 中执行其他常见任务：

如何在 SAS 中执行简单线性回归
如何在 SAS 中执行多元线性回归
如何在 SAS 中执行逻辑回归