如何在 sas 中执行多元线性回归

多元线性回归是一种我们可以用来理解两个或多个预测变量与响应变量之间关系的方法。

本教程介绍如何在 SAS 中执行多元线性回归。

第 1 步：创建数据

假设我们想要拟合一个多元线性回归模型，该模型使用学习时间和练习考试次数来预测学生的期末考试成绩：

考试成绩 = β ₀ + β ₁ （小时）+ β ₂ （预备考试）

首先，我们将使用以下代码创建一个包含 20 名学生信息的数据集：

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

第 2 步：执行多元线性回归

接下来，我们将使用proc reg对数据拟合多元线性回归模型：

 /*fit multiple linear regression model*/
proc reg data =exam_data;
    model score = hours prep_exams;
run ; 

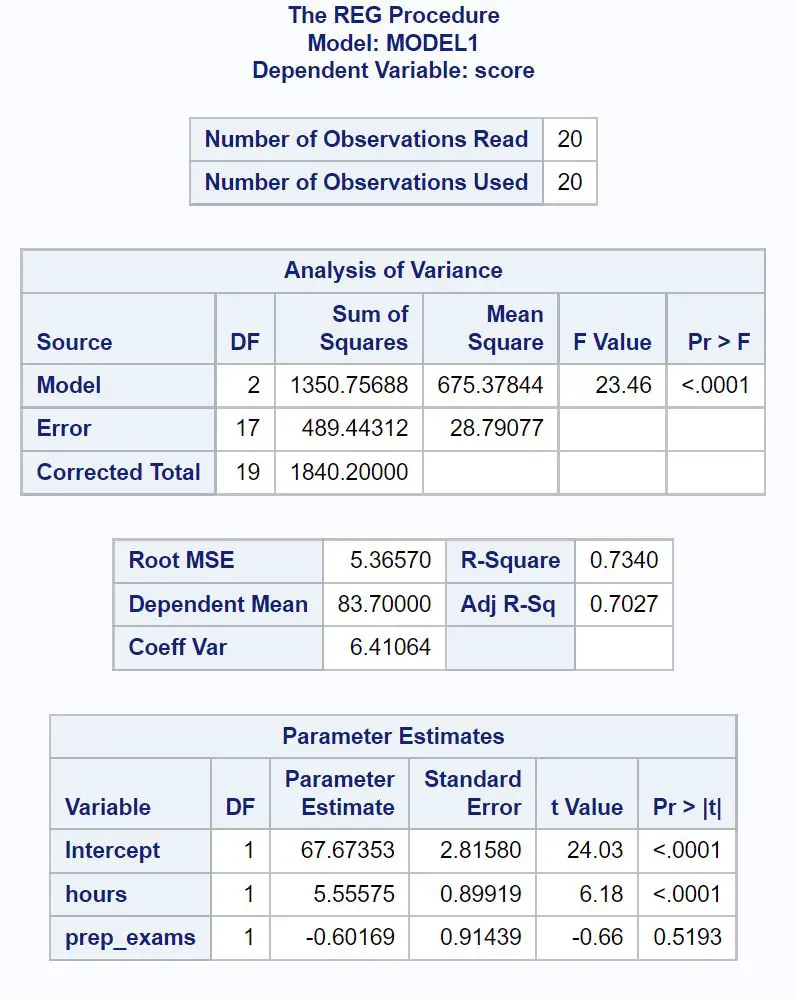
以下是如何解释每个表中最相关的数字：

差距分析表：

回归模型的总体F 值为23.46 ，相应的 p 值为<0.0001 。

由于该 p 值小于 0.05，因此我们得出结论，回归模型作为一个整体具有统计显着性。

模型拟合表：

R 方值告诉我们考试成绩的变化百分比，可以通过学习的小时数和参加的准备考试的次数来解释。

一般来说，回归模型的R 平方值越大，预测变量对响应变量值的预测效果就越好。

在这种情况下， 73.4%的考试成绩差异可以通过学习时数和参加预科考试的次数来解释。

了解Root MSE值也很有用。这表示观测值与回归线之间的平均距离。

在这个回归模型中，观测值与回归线平均偏离5.3657个单位。

参数估计表：

我们可以利用此表中的参数估计值来写出拟合回归方程：

考试成绩 = 67.674 + 5.556*(小时) – 0.602*(prep_exams)

我们可以使用这个方程根据学生的学习小时数和参加的练习考试次数来找到学生的估计考试成绩。

例如，学习 3 小时并参加 2 次预备考试的学生应获得83.1的考试成绩：

预计考试成绩 = 67.674 + 5.556*(3) – 0.602*(2) = 83.1

小时数的 p 值 (<0.0001) 小于 0.05，这意味着它与考试结果具有统计显着相关性。

然而，预备考试的 p 值 (0.5193) 不小于 0.05，这意味着它与考试结果没有统计上显着的关联。

我们可能决定从模型中删除预备考试，因为它们在统计上不显着，而是使用学习时间作为唯一的预测变量来执行简单的线性回归。

其他资源

以下教程解释了如何在 SAS 中执行其他常见任务：

如何在SAS中计算相关性
如何在 SAS 中执行简单线性回归
如何在 SAS 中执行单向方差分析