如何在 sas 中执行多项式回归
最常见的回归分析类型是简单线性回归,当预测变量和响应变量具有线性关系时使用。
然而,有时预测变量和响应变量之间的关系是非线性的。
在这些情况下,使用多项式回归是有意义的,它可以解释变量之间的非线性关系。
以下示例显示如何在 SAS 中执行多项式回归。
示例:SAS 中的多项式回归
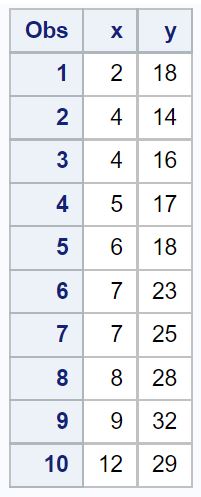
假设我们在 SAS 中有以下数据集:
/*create dataset*/ data my_data; input xy; datalines ; 2 18 4 14 4 16 5 17 6 18 7 23 7 25 8 28 9 32 12 29 ; run ; /*view dataset*/ proc print data =my_data;
现在假设我们创建一个散点图来可视化数据集中变量 x 和 y 之间的关系:
/*create scatter plot of x vs. y*/
proc sgplot data =my_data;
scatter x =x y =y;
run ;
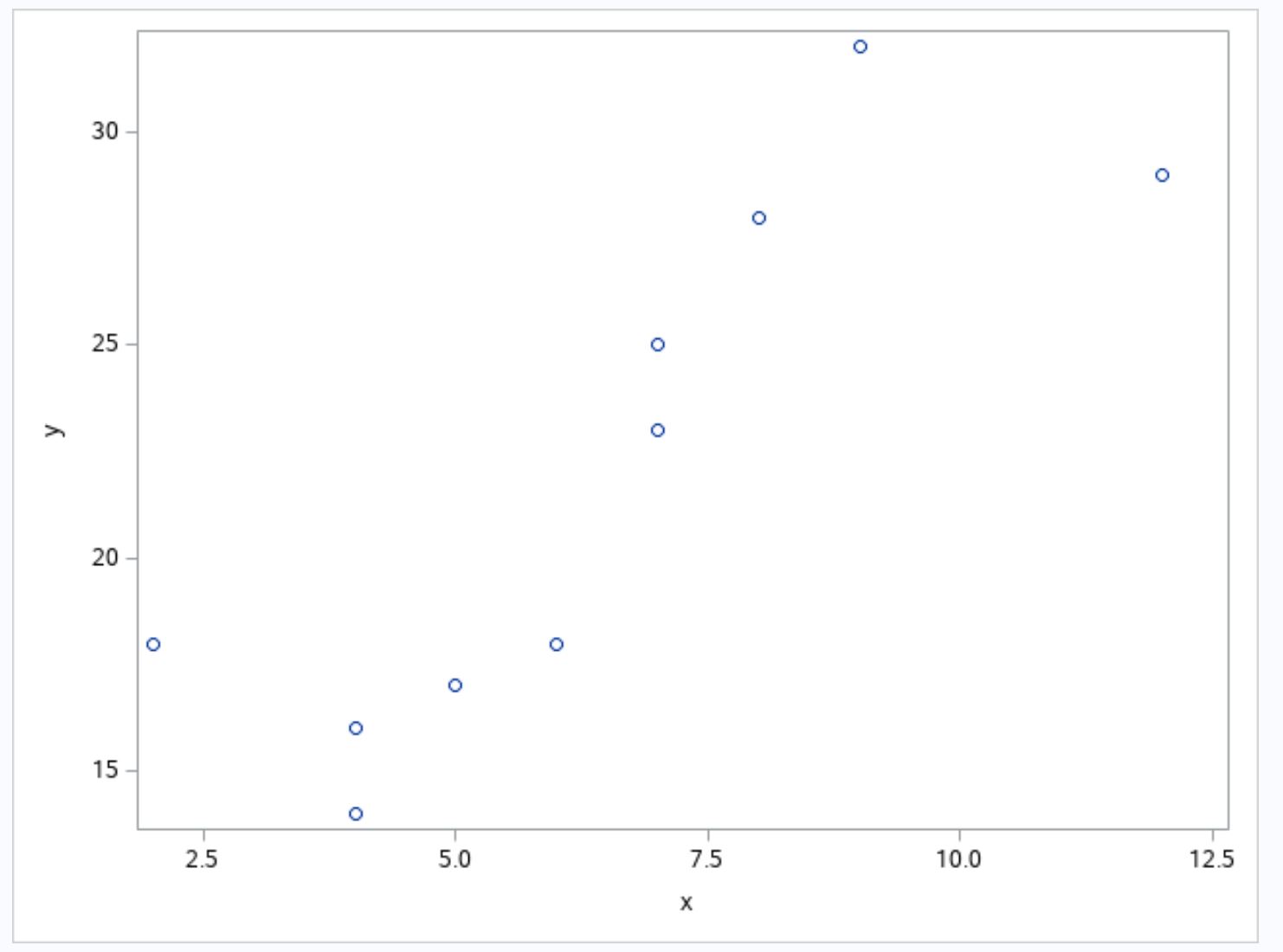
从图中我们可以看出,x 和 y 之间呈三次关系。
因此,我们可以在数据集中定义两个新的预测变量(x 2和 x 3 ),然后使用proc reg使用这些预测变量来拟合多项式回归模型:
/*create dataset with new predictor variables*/ data my_data; input xy; x2 = x** 2 ; x3 = x** 3 ; datalines ; 2 18 4 14 4 16 5 17 6 18 7 23 7 25 8 28 9 32 12 29 ; run ; /*fit polynomial regression model*/ proc reg data =my_data; model y = x x2 x3; run ;
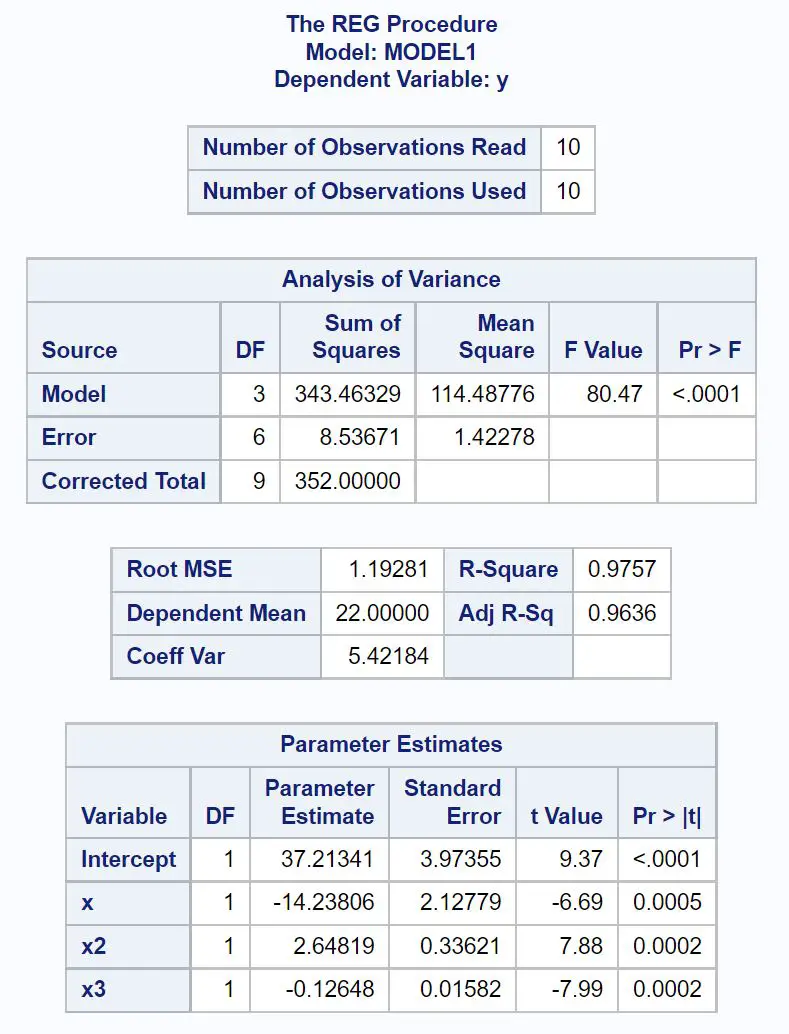
从参数估计表中,我们可以找到系数估计并将我们的拟合多项式回归方程写为:
y = 37.213 – 14.238x + 2.648x 2 – 0.126x 3
在给定预测变量值的情况下,该方程可用于查找响应变量的期望值。
例如,如果 xa 的值为 4,则 y 的值为 14.565:
y = 37.213 – 14.238(4) + 2.648(4) 2 – 0.126(4) 3 = 14.565
我们还可以看到,多项式回归模型的调整后 R 平方值为0.9636 ,该值非常接近 1,这表明该模型在拟合数据集方面做得非常出色。
其他资源
以下教程解释了如何在 SAS 中执行其他常见任务: