如何在 sas 中计算优势比（附示例）

在统计学中，优势比告诉我们治疗组中发生事件的几率与对照组中发生事件的几率之比。

在对 2 × 2 表进行分析时，我们经常计算优势比，其格式如下：

要计算 SAS 中的优势比，我们可以使用PROC FREQ语句。

下面的例子展示了如何在实践中使用这个语句。

示例：计算 SAS 中的优势比

假设 50 名篮球运动员正在使用新的训练计划，50 名篮球运动员正在使用旧的训练计划。在节目结束时，我们会测试每个玩家，看看他们是否通过了特定的技能测试。

下表显示了通过和失败的玩家数量（基于他们使用的程序）：

假设我们要计算优势比来比较玩家使用新程序与使用旧程序通过技能测试的机会。

我们可以将以下语法与 SAS 中的PROC FREQ结合使用，并结合chisq和relrisk指令来计算优势比以及相对风险值：

 /*create dataset*/
data my_data;
    input result $program $count;
    datalines ;
Passed New 34
Passed Old 39
_Failed New 16
_Failed Old 11
;
run ;
/*calculate odds ratio*/
proc freq data =my_data;
    weightcount ;
    tables program * result / chisq relrisk ;
run ;

结果的第一个表显示了每个分类变量组合的频率：

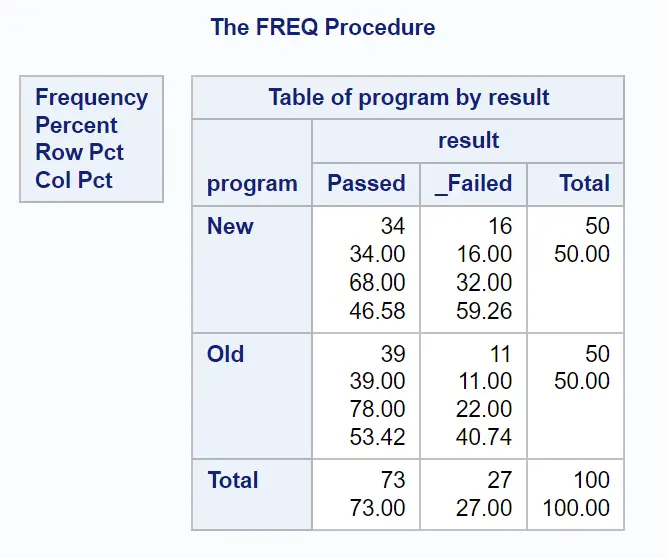
结果的最后一个表显示了我们感兴趣的优势比：

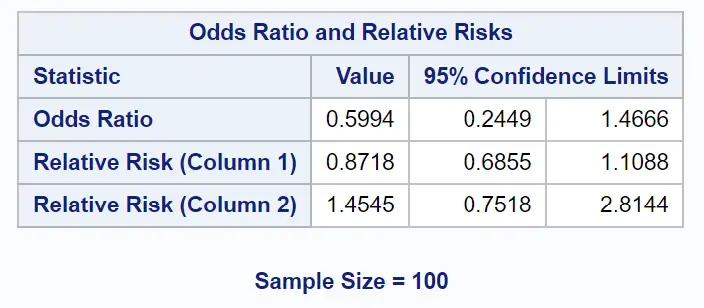
优势比为0.5994 。

我们将此解释为，使用新程序的玩家通过测试的几率仅为使用旧程序的玩家通过测试的几率的 0.5994 倍。

换句话说，通过使用新程序，玩家通过测试的几率实际上降低了约40.06%。

我们还可以使用“结果95% 置信限”列中的值来构建以下优势比的 95% 置信区间：

优势比的 95% 置信区间： [0.2449, 1.4666] 。

我们 95% 确信新旧训练计划之间的真实优势比包含在该区间内。

由于置信区间包含优势比值为 1，这意味着优势比不具有统计显着性。

换句话说，我们从优势比得知，玩家使用新程序的成功机会低于使用旧程序的成功机会，但这些机会之间的差异实际上在统计上并不显着。

其他资源

以下教程提供了有关优势比的其他信息：

比值比和相对风险之间的差异
完整指南：如何报告优势比
如何计算优势比的置信区间