如何在 sas 中计算 aic（附示例）

赤池信息准则 (AIC) 是用于比较多个回归模型拟合度的指标。

计算方法如下：

AIC = 2K – 2 ln (L)

金子：

• K：模型参数的数量。 K 的默认值为 2，因此只有一个预测变量的模型的 K 值为 2+1 = 3。
• ln (L) ：模型的对数似然。大多数统计软件可以自动为您计算该值。

AIC 旨在找到解释数据变化最大的模型，同时惩罚使用过多参数的模型。

拟合多个回归模型后，您可以比较每个模型的 AIC 值。 AIC越低，模型越适合。

以下示例显示如何计算 SAS 中不同回归模型的 AIC。

示例：如何在 SAS 中计算 AIC

假设我们想要拟合三种不同的多元线性回归模型来预测学生在班级中将取得的考试成绩。

以下是我们将在每个模型中使用的预测变量：

• 模型 1 中的预测变量：学习时间
• 模型 2 中的预测变量：过去的实际考试
• 模型 3 中的预测变量：学习和练习考试所花费的时间

首先，我们将使用以下代码创建一个包含 20 名学生信息的数据集：

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

接下来，我们将使用proc reg来拟合这些回归模型中的每一个，并且我们将使用Selection=adjrsq sse aic语句来计算每个模型的 AIC 值：

 /*fit multiple linear regression models and calculate AIC for each model*/
proc reg data =exam_data;
    model score = hours prep_exams / selection=adjrsq sse aic;
run ; 

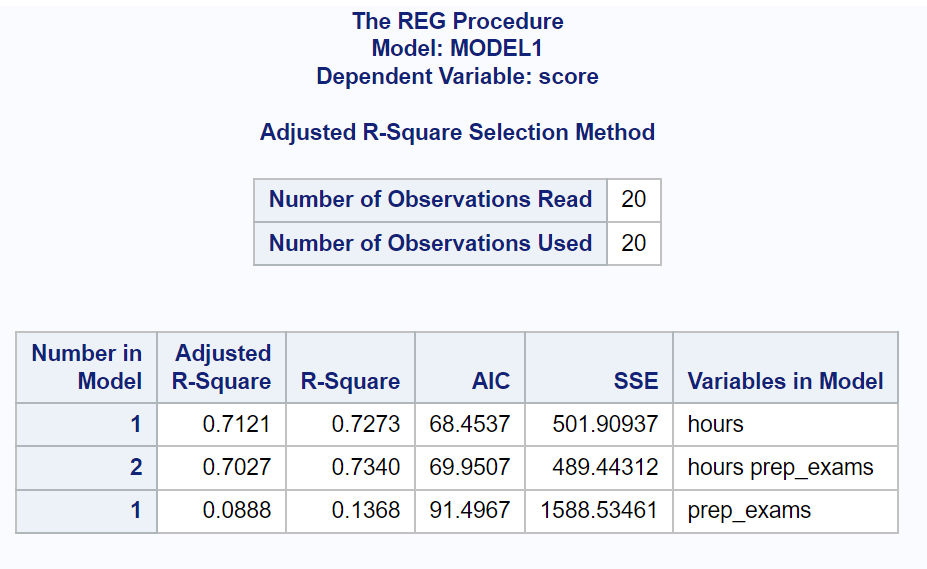
从结果中我们可以看到每个模型的AIC值：

• 以小时为预测变量的 AIC： 68.4537
• 以学时和考试作为预测变量的 AIC： 69.9507
• 以考试为预测变量的 AIC： 91.4967

AIC 值最低的模型是仅包含小时数作为预测变量的模型。

因此，我们声明以下模型最适合数据：

分数 = β ₀ + β ₁ （学习时间）

一旦我们确定该模型是最佳模型，我们就可以对其进行拟合并分析结果（包括 R 平方值和 beta 系数），以确定学习时间和学生成绩之间的确切关系。 ‘期末考试。

其他资源

以下教程解释了如何在 SAS 中执行其他常见任务：

如何在 SAS 中执行简单线性回归
如何在 SAS 中执行多元线性回归
如何在 SAS 中计算 R 平方
如何在 SAS 中计算 RMSE