如何在 sas 中执行简单线性回归

简单线性回归是一种我们可以用来理解预测变量和响应变量之间关系的技术。

该技术找到一条最“适合”数据的线，并采用以下形式：

ŷ = b ₀ + b ₁ x

金子：

• ŷ : 估计响应值
• b ₀ ：回归线的原点
• b ₁ ：回归线的斜率

这个方程帮助我们理解预测变量和响应变量之间的关系。

以下分步示例展示了如何在 SAS 中执行简单线性回归。

第 1 步：创建数据

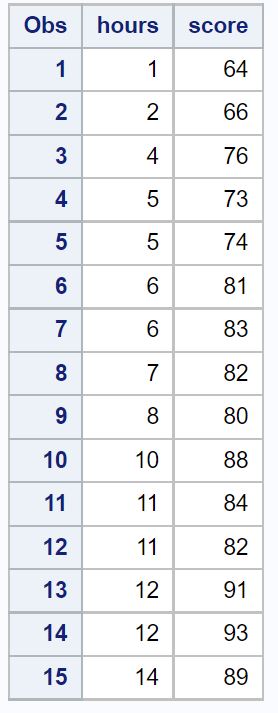
在此示例中，我们将创建一个数据集，其中包含 15 名学生的学习总时数和期末考试成绩。

我们将使用小时作为预测变量并使用分数作为响应变量来拟合一个简单的线性回归模型。

以下代码显示了如何在 SAS 中创建此数据集：

 /*create dataset*/
data exam_data;
    input hours score;
    datalines ;
1 64
2 66
4 76
5 73
5 74
6 81
6 83
7 82
8 80
10 88
11 84
11 82
12 91
12 93
14 89
;
run ;

/*view dataset*/
proc print data =exam_data;

步骤 2：拟合简单线性回归模型

接下来，我们将使用proc reg来拟合简单线性回归模型：

 /*fit simple linear regression model*/
proc reg data =exam_data;
   model score = hours;
run ; 

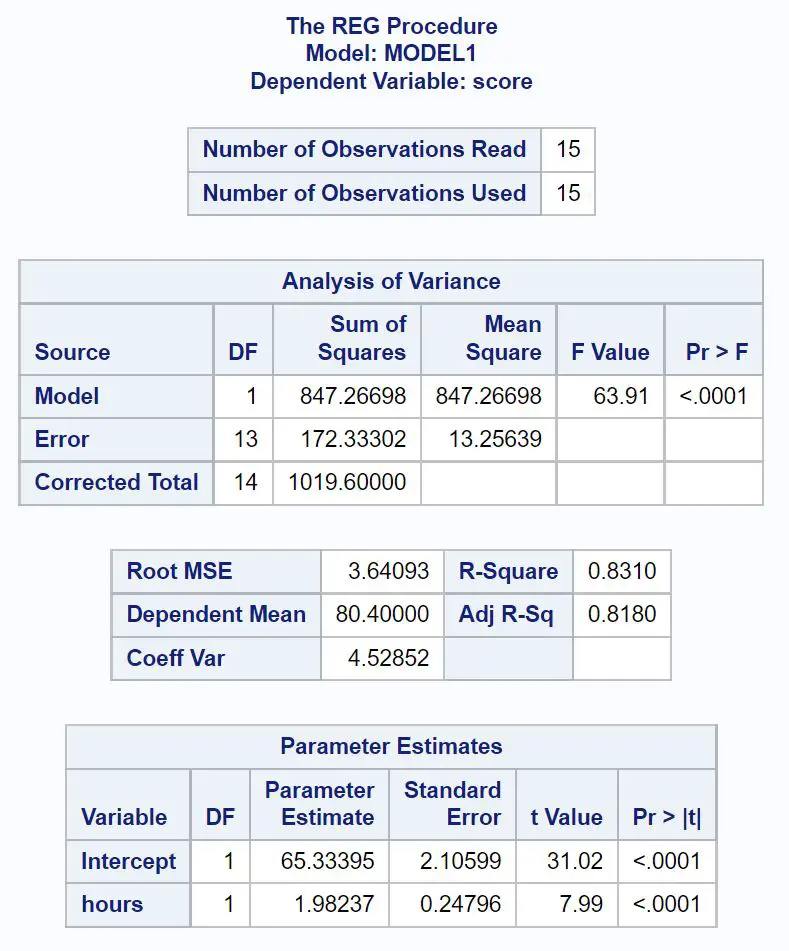
以下是如何解释结果中每个表中最重要的值：

差距分析表：

回归模型的总体F 值为63.91 ，相应的 p 值为<0.0001 。

由于该 p 值小于 0.05，因此我们得出结论，回归模型作为一个整体具有统计显着性。换句话说，时间是预测考试结果的有用变量。

模型拟合表：

R 方值告诉我们可以通过学习小时数来解释的考试成绩变化百分比。

一般来说，回归模型的R 平方值越大，预测变量对响应变量值的预测效果就越好。

在这种情况下， 83.1%的考试成绩差异可以用学习时数来解释。这个值相当高，表明学习时间是预测考试结果的一个非常有用的变量。

参数估计表：

从该表我们可以看到拟合的回归方程：

分数 = 65.33 + 1.98*（小时）

我们将此解释为意味着每多学习一小时，考试成绩就会平均提高1.98 分。

原始值告诉我们零学时学生的平均考试成绩是65.33 。

我们还可以使用这个方程根据学生学习的小时数找到预期的考试成绩。

例如，学习 10 小时的学生应获得85.13的考试成绩：

分数 = 65.33 + 1.98*(10) = 85.13

由于此表中小时的 p 值 (<0.0001) 小于 0.05，因此我们得出结论，这是一个具有统计显着性的预测变量。

第 3 步：分析残差图

简单线性回归对模型残差做出两个重要假设：

• 残差呈正态分布。
• 残差在预测变量的每个水平上具有相等的方差（“同方差”）。

如果不满足这些假设，那么我们的回归模型的结果可能不可靠。

为了验证是否满足这些假设，我们可以分析 SAS 自动在输出中显示的残差图：

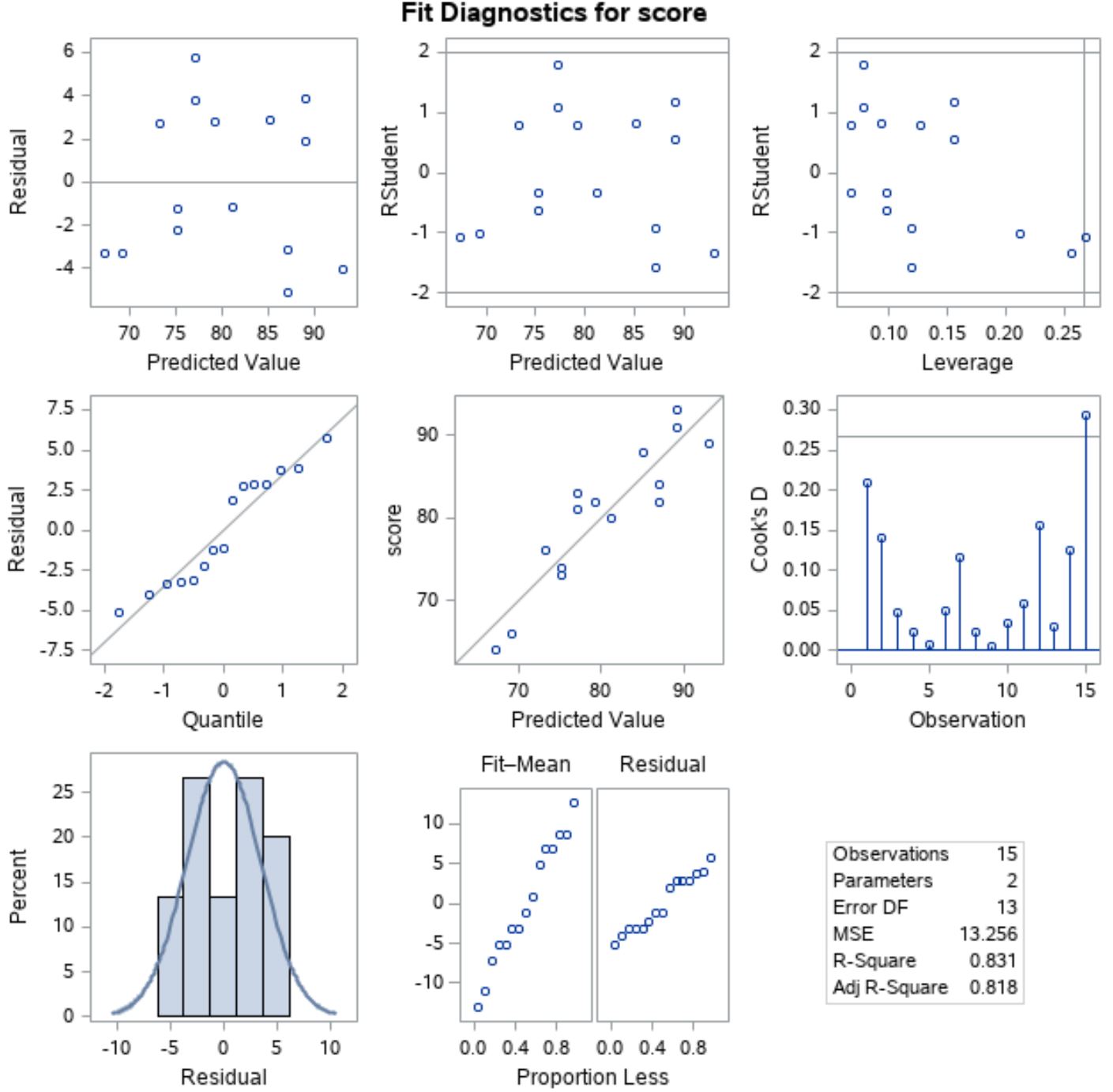
为了验证残差是否服从正态分布，我们可以分析中线左侧位置的图，其中 x 轴为“分位数”，y 轴为“残差”。

该图称为QQ 图，是“分位数-分位数”的缩写，用于确定数据是否服从正态分布。如果数据呈正态分布，QQ 图上的点将位于一条直线对角线上。

从图中我们可以看到这些点大致沿着直线对角线分布，因此我们可以假设残差呈正态分布。

接下来，为了验证残差是否是同方差的，我们可以查看第一行左侧位置的图，其中 x 轴为“预测值”，y 轴为“残差”。

如果绘图点随机散布在零周围，没有清晰的模式，那么我们可以假设残差是同方差的。

从图中我们可以看到，点随机散布在零周围，整个图中每个级别的方差近似相等，因此我们可以假设残差是同方差的。

由于满足两个假设，我们可以假设简单线性回归模型的结果是可靠的。

其他资源

以下教程解释了如何在 SAS 中执行其他常见任务：

如何在 SAS 中执行单向方差分析
如何在 SAS 中执行双向方差分析
如何在SAS中计算相关性