斯内装饰 f 分销
本文介绍了 Snedecor F 发行版是什么以及它的用途。此外,您将能够看到 Snedecor F 分布图及其统计特性。
什么是斯内装饰 F 分布?
Snedecor F 分布,也称为Fisher–Snedecor F 分布或简称F 分布,是一种用于统计推断,特别是方差分析的连续概率分布。
Snedecor F 分布的属性之一是它由两个实数参数m和n的值定义,这两个实数参数表示它们的自由度。因此,Snedecor 分布 F 的符号为F m,n ,其中m和n是定义分布的参数。

![Rendered by QuickLaTeX.com \left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d407869e61ca4357ffbcb40df3bd83ab_l3.png)
➤请参阅:什么是卡方分布?
Fisher-Snedecor F 分布得名于英国统计学家 Ronald Fisher 和美国统计学家 George Snedecor。
在统计学中,Fisher-Snedecor F 分布有不同的应用。例如,Fisher-Snedecor F 分布用于比较不同的线性回归模型,该概率分布用于方差分析 (ANOVA)。
Snedecor F分布图
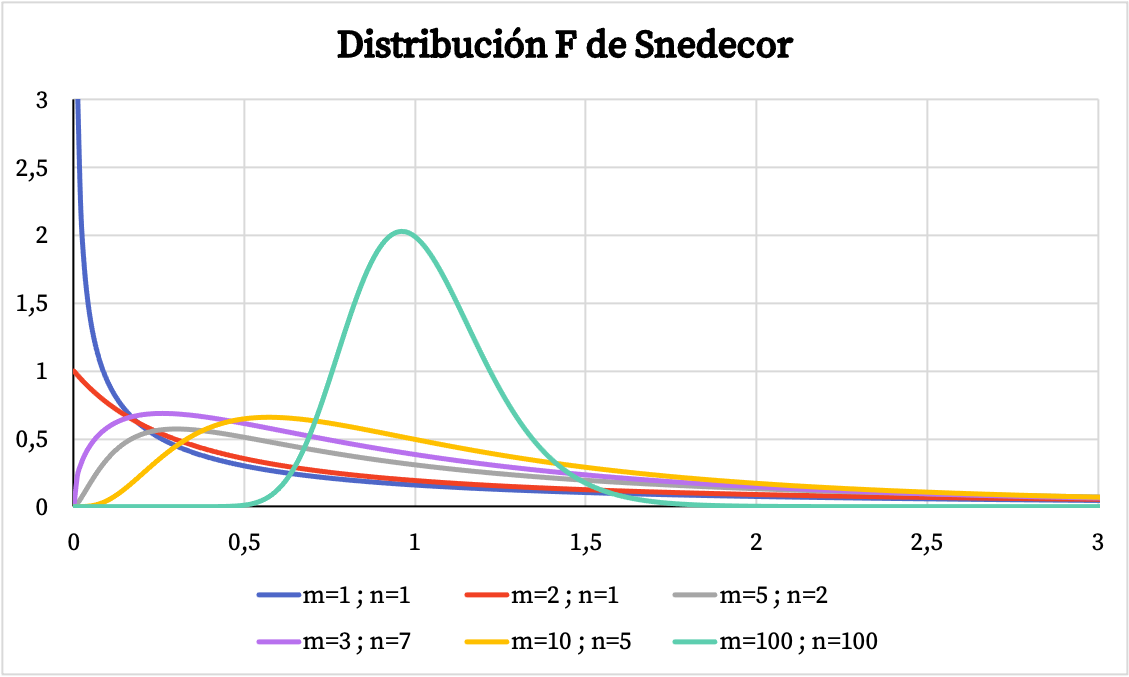
一旦我们了解了 Snedecor F 分布的定义,其密度函数图和累积概率图如下所示。
在下图中,您可以看到几个具有不同自由度的 Snedecor F 分布示例。
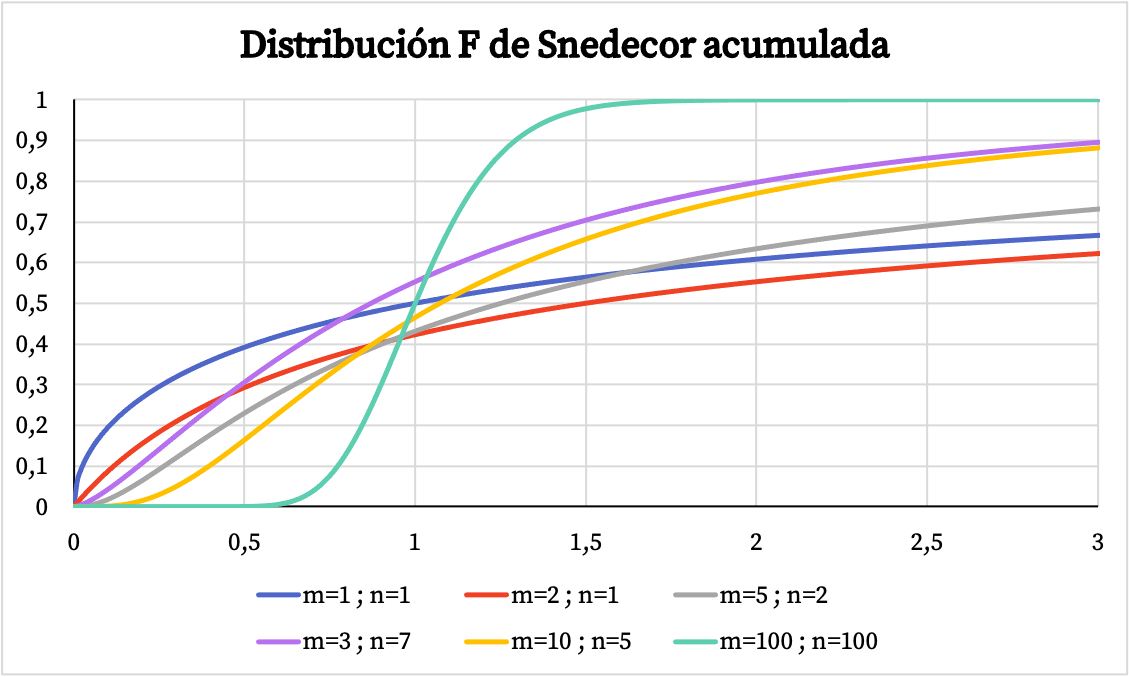
另一方面,在下图中,您可以看到 Snedecor F 分布的累积概率函数图如何根据其特征值而变化。
Snedecor F 分布的特征
最后,本节介绍了 Snedecor F 发行版最重要的特征。
- Snedecor F 分布的自由度m和n是定义分布形状的两个参数。 Snedecor F分布的这些特征值为正整数。
![\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”68″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> Snedecor F 分布的域由所有大于或等于零的实数组成。</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-043df156b055e7088fa83fe733825632_l3.png)
![]()
- 对于大于 2 的n值,Snedecor F 分布的平均值等于n减去n减 2。
![\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”225″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li>当参数<em>n</em>大于2时,Snedecor分布F的方差可以通过应用以下公式计算:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5861b8fbc6e7aef8cac0eb21cad00c9f_l3.png)
![\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} ” title=”Rendered by QuickLaTeX.com” height=”80″ width=”366″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li>如果参数<em>m</em>大于2,则Snedecor分布F的众数可以用以下表达式计算:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-9a284413da889eec7ac2e9a95e255169_l3.png)
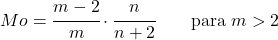
![Rendered by QuickLaTeX.com \displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-06871a7baaf462b75f545a02eac7dd11_l3.png)
- 如果变量遵循自由度为m和n的 Snedecor F 分布,则所述变量的反函数遵循具有相同自由度但改变其值顺序的 Snedecor F 分布。
![]()
- Student 分布与 Snedecor F 分布有以下关系:
![]()
➤请参阅:学生 t 分布是什么?