如何在 spss 中创建协方差矩阵

协方差是衡量一个变量的变化与第二个变量的变化如何关联的指标。更具体地说，它是两个变量线性相关程度的度量。

计算两个变量X和Y之间的协方差的公式为：

COV( X , Y ) = Σ(x- x )(y- y ) / n

协方差矩阵是一个方阵，显示数据集中不同变量之间的协方差。

本教程介绍如何在 SPSS 中为给定数据集创建协方差矩阵。

示例：SPSS 中的协方差矩阵

假设我们有以下数据集，显示 10 名不同学生在数学、科学和历史这三个科目中的测试成绩：

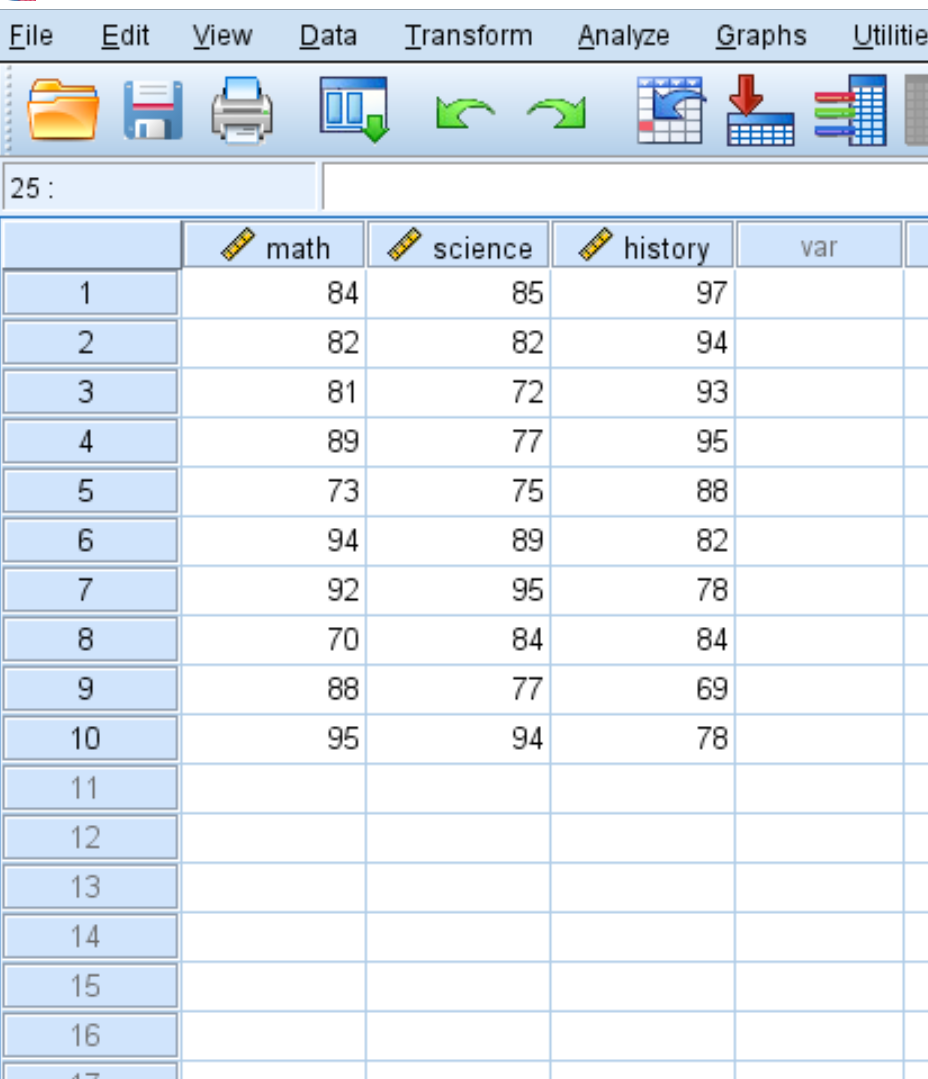
要为此数据集创建协方差矩阵，请单击“分析”选项卡，然后单击“关联” ，然后单击“双变量” ：

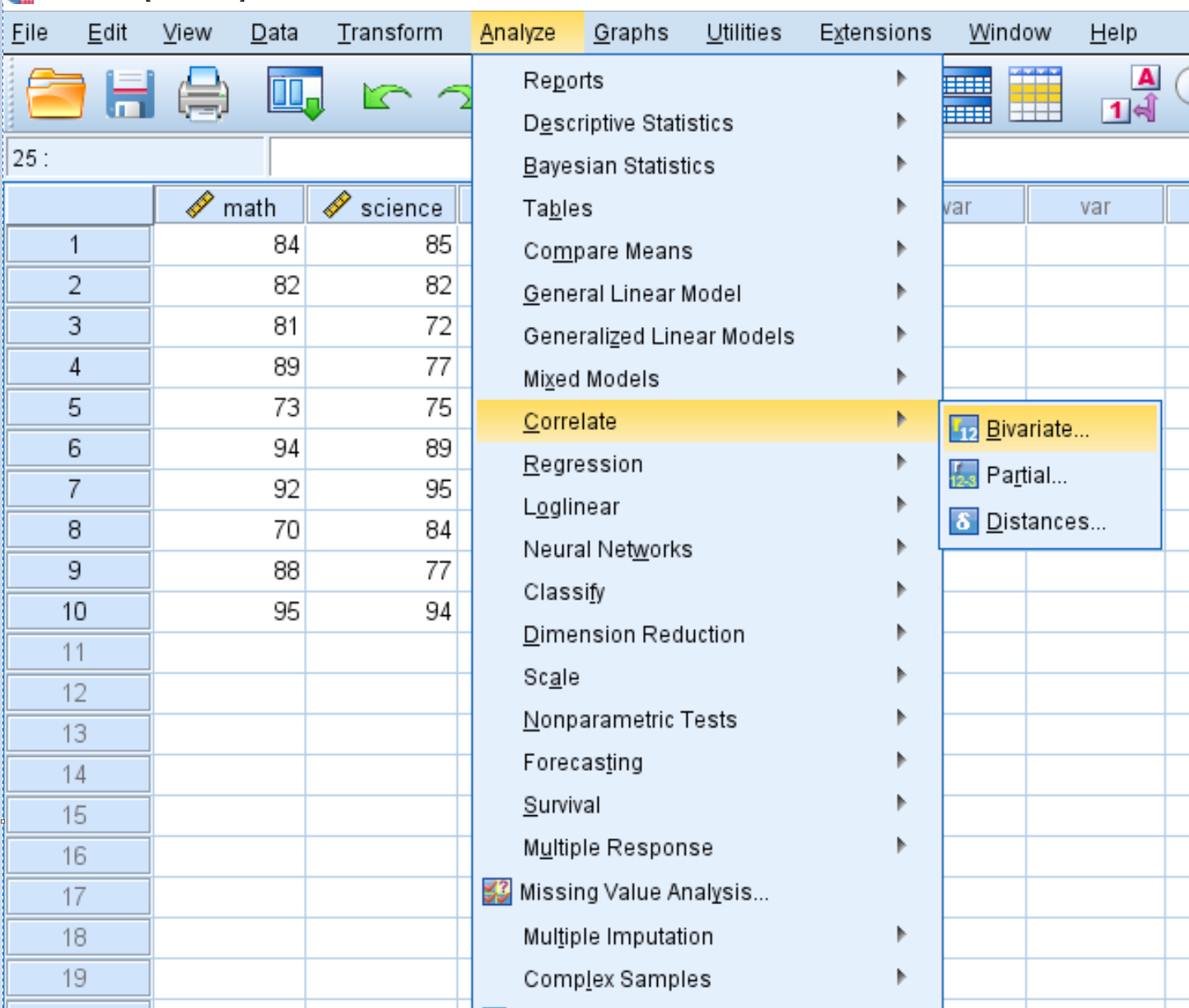
在出现的新窗口中，将三个变量分别拖到标记为Variables的框中：

接下来，单击“选项” 。选中产品之间的方差和协方差旁边的框。然后单击“继续” 。

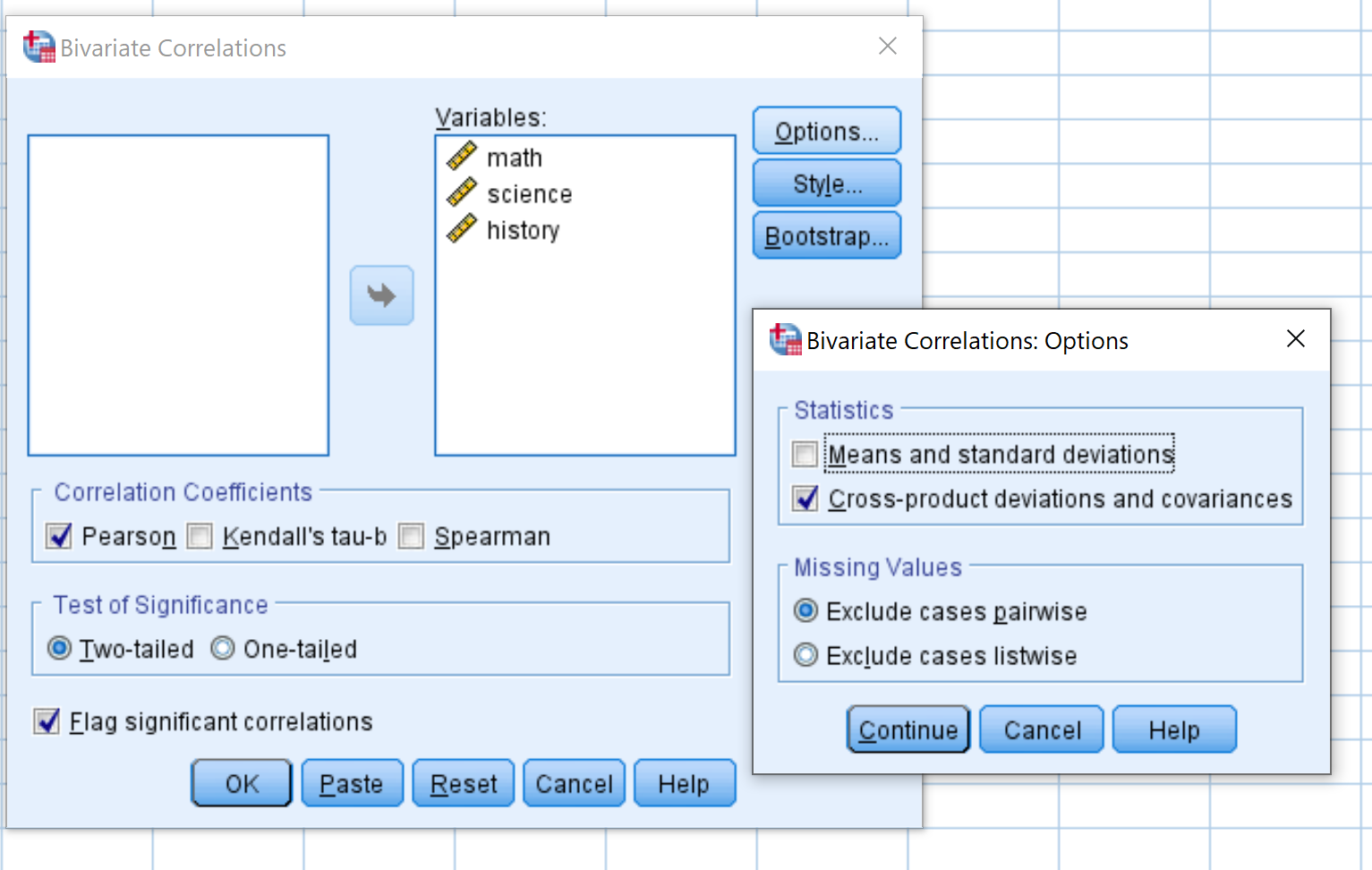
然后单击“确定” 。结果将出现在新窗口中：

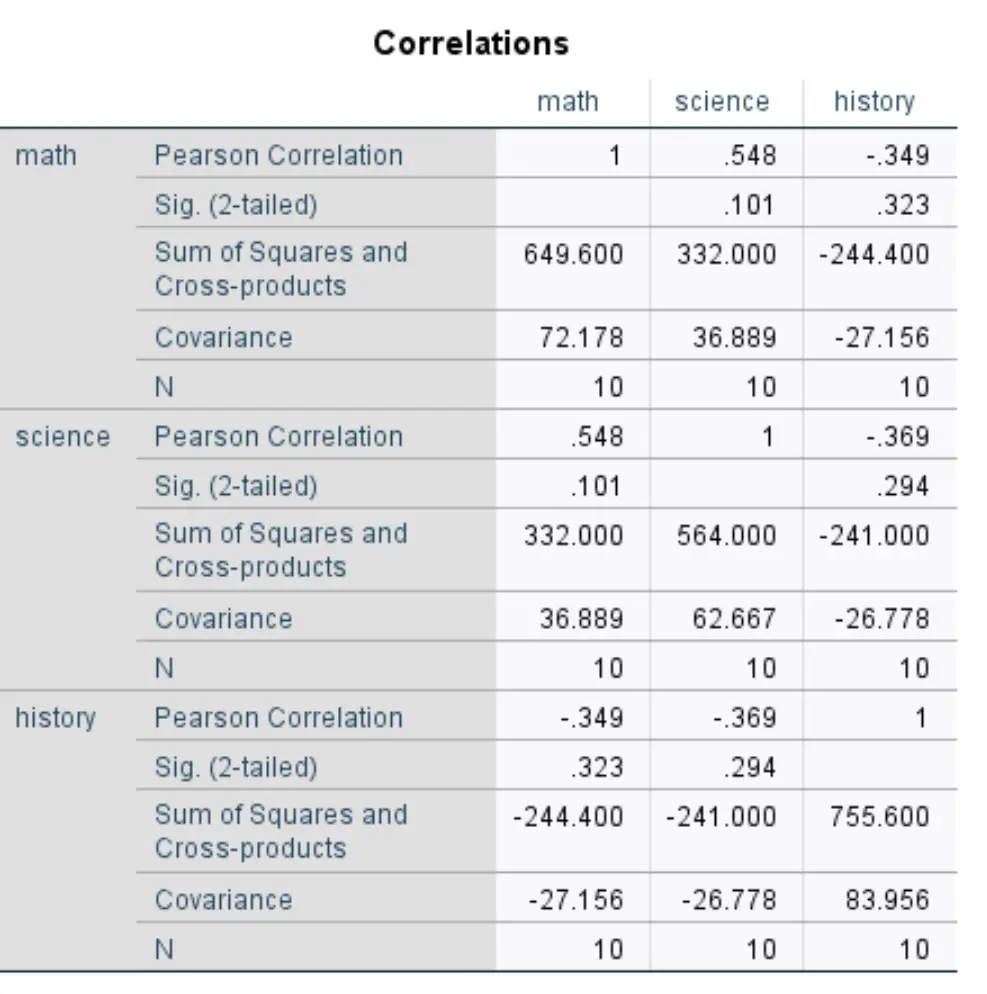
要获得变量的每个成对组合的协方差，您需要将平方和和向量乘积除以N。

例如，数学和科学之间的协方差可以计算如下：

COV（数学、科学）= 332,000 / 10 = 33.2 。

同样，数学和历史之间的协方差可以计算如下：

COV（数学、历史）= -244.400 / 10 = -24.44 。

您还可以通过将平方和和向量乘积除以N来获得每个变量的方差。

例如，数学上的方差可以计算如下：

VAR（数学）= 649.600 / 10 = 64.96 。

您可以通过执行类似的计算来获取该数据集的完整协方差矩阵：

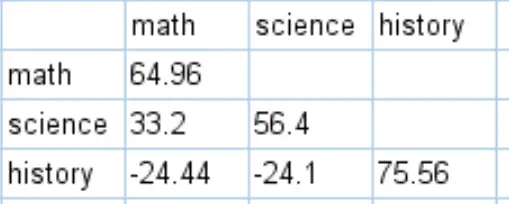
如何解释协方差矩阵

协方差矩阵对角线上的值就是每个受试者的方差。例如：

• 数学结果的方差为64.96 。
• 科学分数的方差是56.4 。
• 历史分数的方差为75.56 。

矩阵的其他值代表不同主体之间的协方差。例如：

• 数学和科学分数之间的协方差为33.2 。
• 数学和历史分数之间的协方差为-24.44 。
• 科学和历史分数之间的协方差为-24.1 。

协方差为正数表示两个变量倾向于同时增加或减少。例如，数学和科学具有正协方差 (33.2)，表明数学得分高的学生也往往在科学得分高。同样，数学成绩不佳的学生在科学方面也往往表现不佳。

协方差为负数表示随着一个变量的增加，第二个变量趋于减少。例如，科学和历史具有负协方差（-24.1），表明科学得分高的学生往往在历史得分较低。同样，科学得分低的学生往往在历史得分高。

其他资源

如何在 SPSS 中创建相关矩阵
如何在SPSS中计算偏相关