如何在 spss 中创建相关矩阵

相关矩阵是一个方表，显示数据集中不同变量之间的皮尔逊相关系数。

提醒一下，皮尔逊相关系数是两个变量之间线性关联的度量。它的值介于 -1 和 1 之间，其中：

• -1 表示两个变量之间完全负线性相关
• 0 表示两个变量之间不存在线性相关
• 1 表示两个变量之间存在完全正线性相关

相关系数离零越远，两个变量之间的相关性越强。

本教程介绍如何在 SPSS 中创建和解释相关矩阵。

示例：如何在 SPSS 中创建相关矩阵

按照以下步骤为此数据集创建一个相关矩阵，显示八名篮球运动员的平均助攻、篮板和得分：

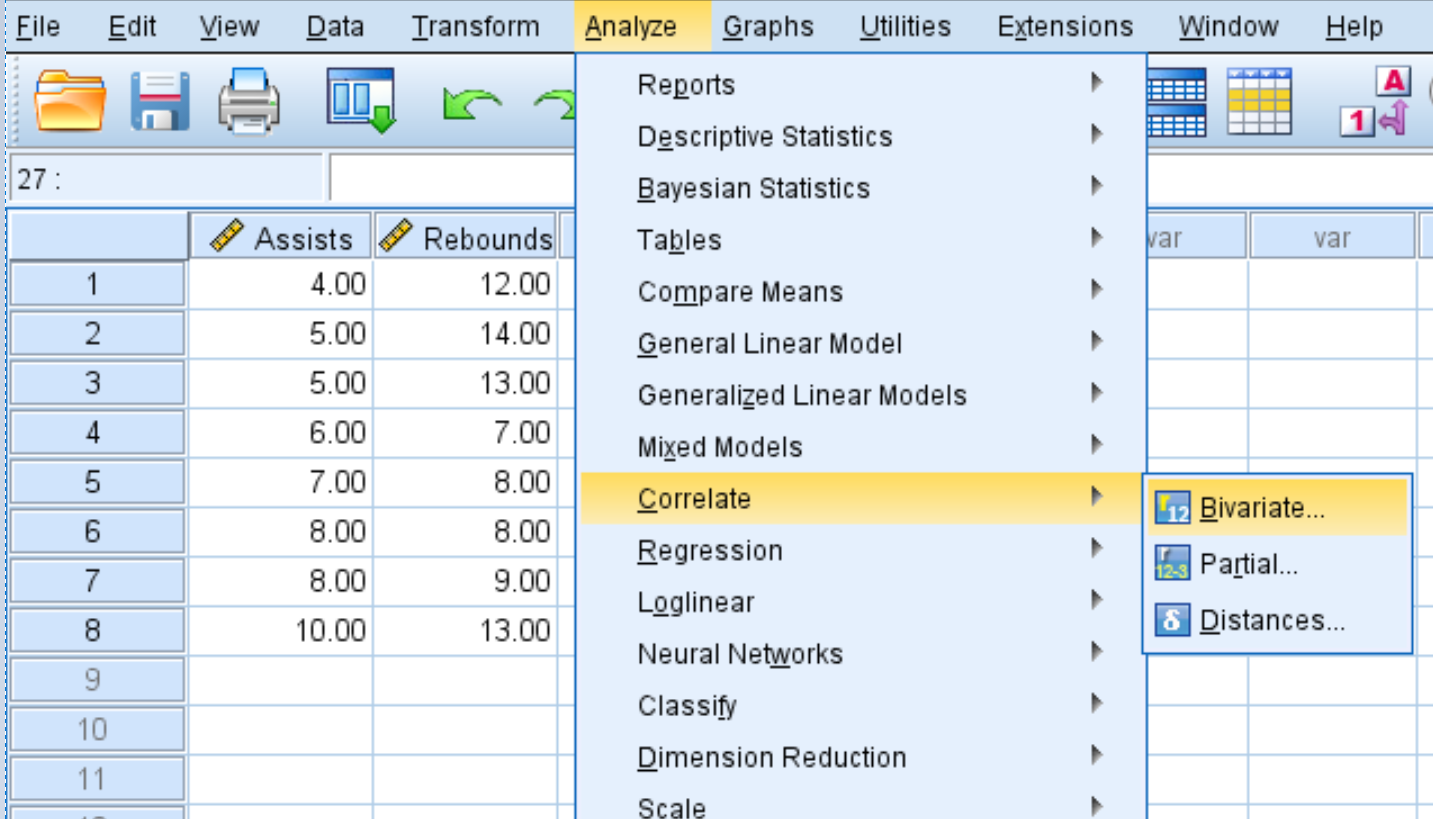
步骤 1：选择二元相关性。

• 单击分析选项卡。
• 单击“关联” 。
• 单击双变量。

步骤 2：创建相关矩阵。

数据集中的每个变量最初将显示在左侧框中：

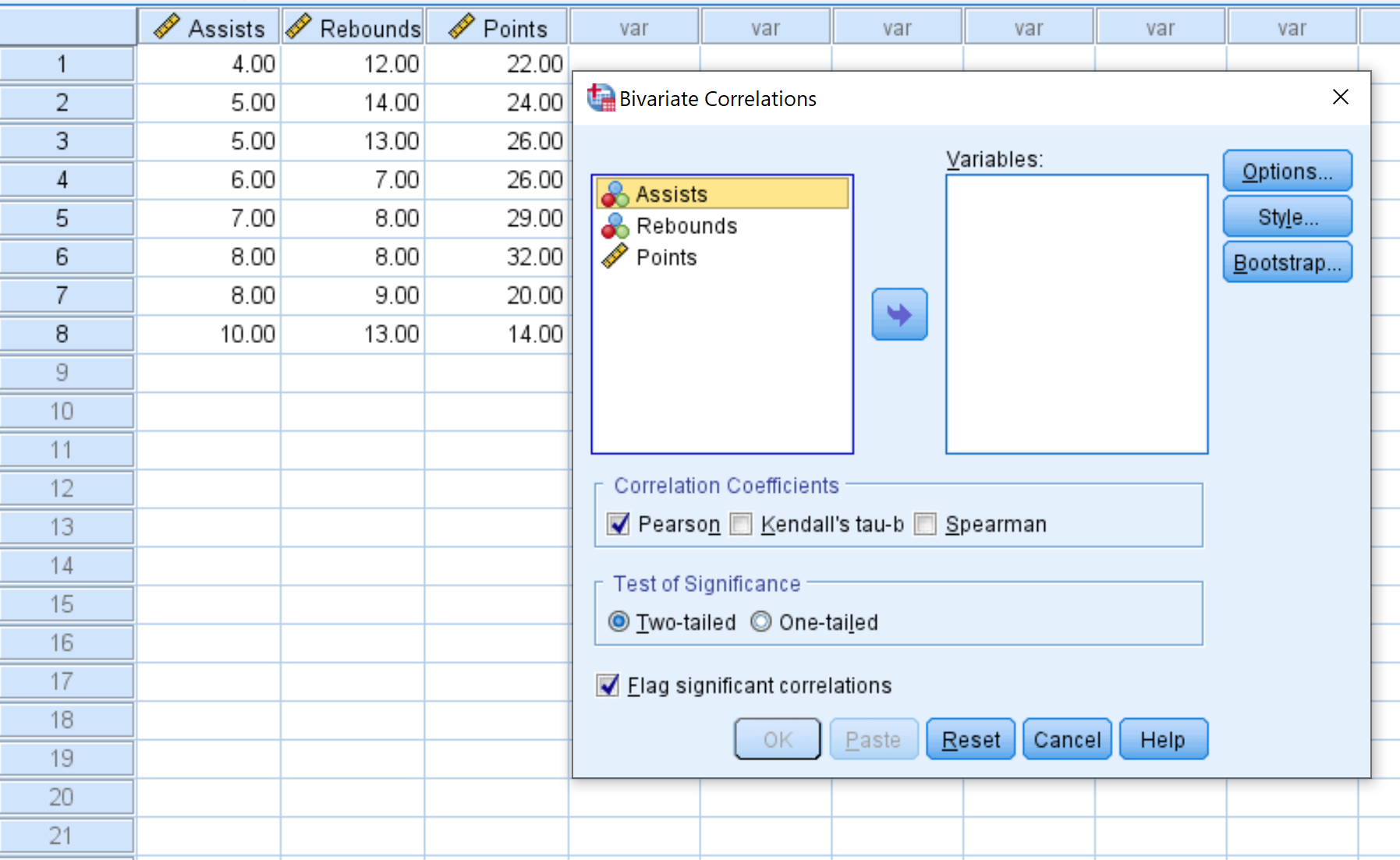
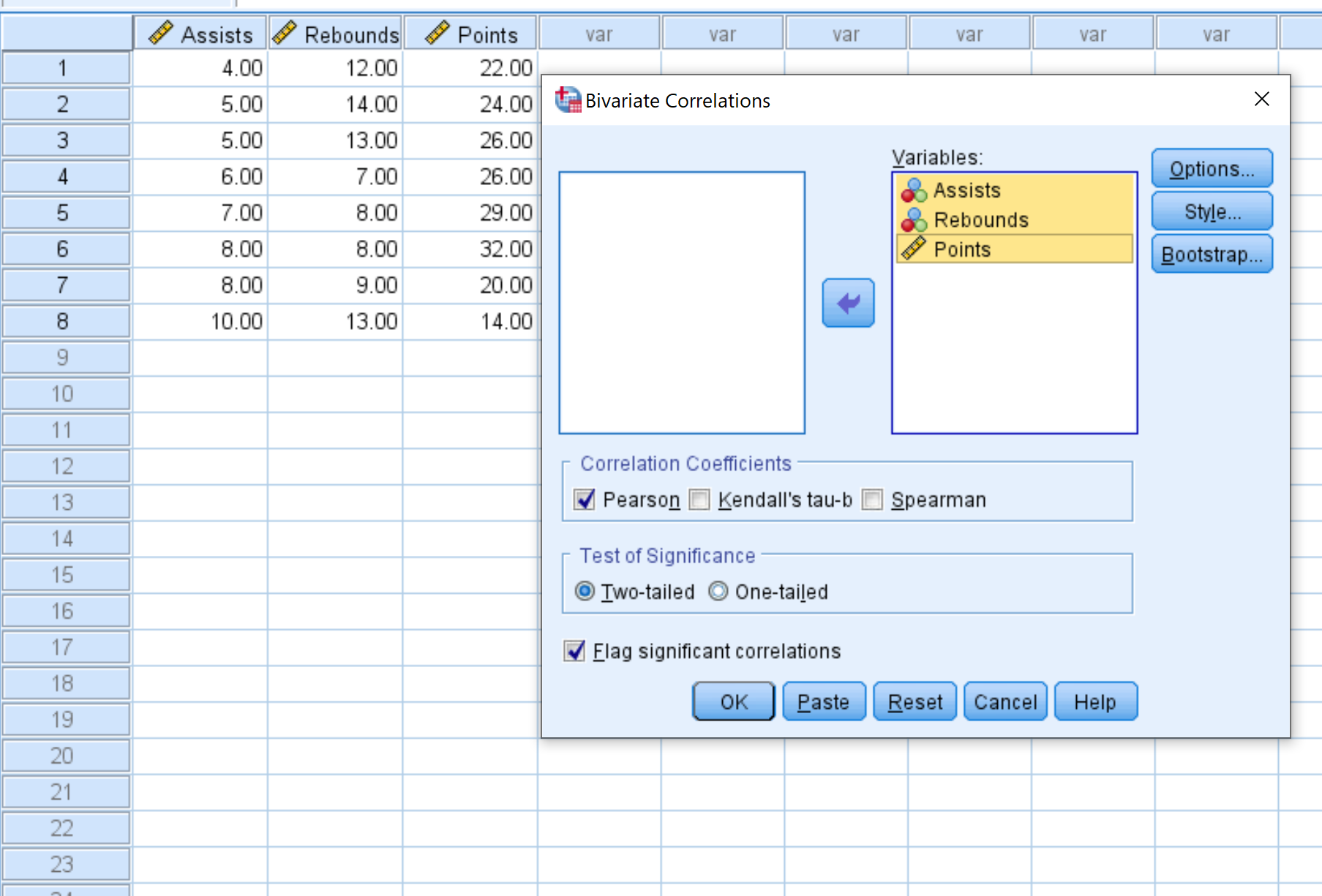
• 选择要包含在相关矩阵中的每个变量，然后单击箭头将它们传输到“变量”框中。我们将在此示例中使用所有三个变量。
• 在“相关系数”下，选择是否要使用 Pearson 相关性、Kendall tau 相关性或 Spearman 相关性。在本例中，我们将其保留为 Pearson。
• 在显着性检验下，选择是否要使用双尾检验或单尾检验来确定两个变量是否具有统计显着关联。我们将其保留为双尾。
• 如果您希望 SPSS报告显着相关的变量，请选中报告显着相关性旁边的框。
• 最后，单击“确定” 。

单击“确定”后，将出现以下相关矩阵：

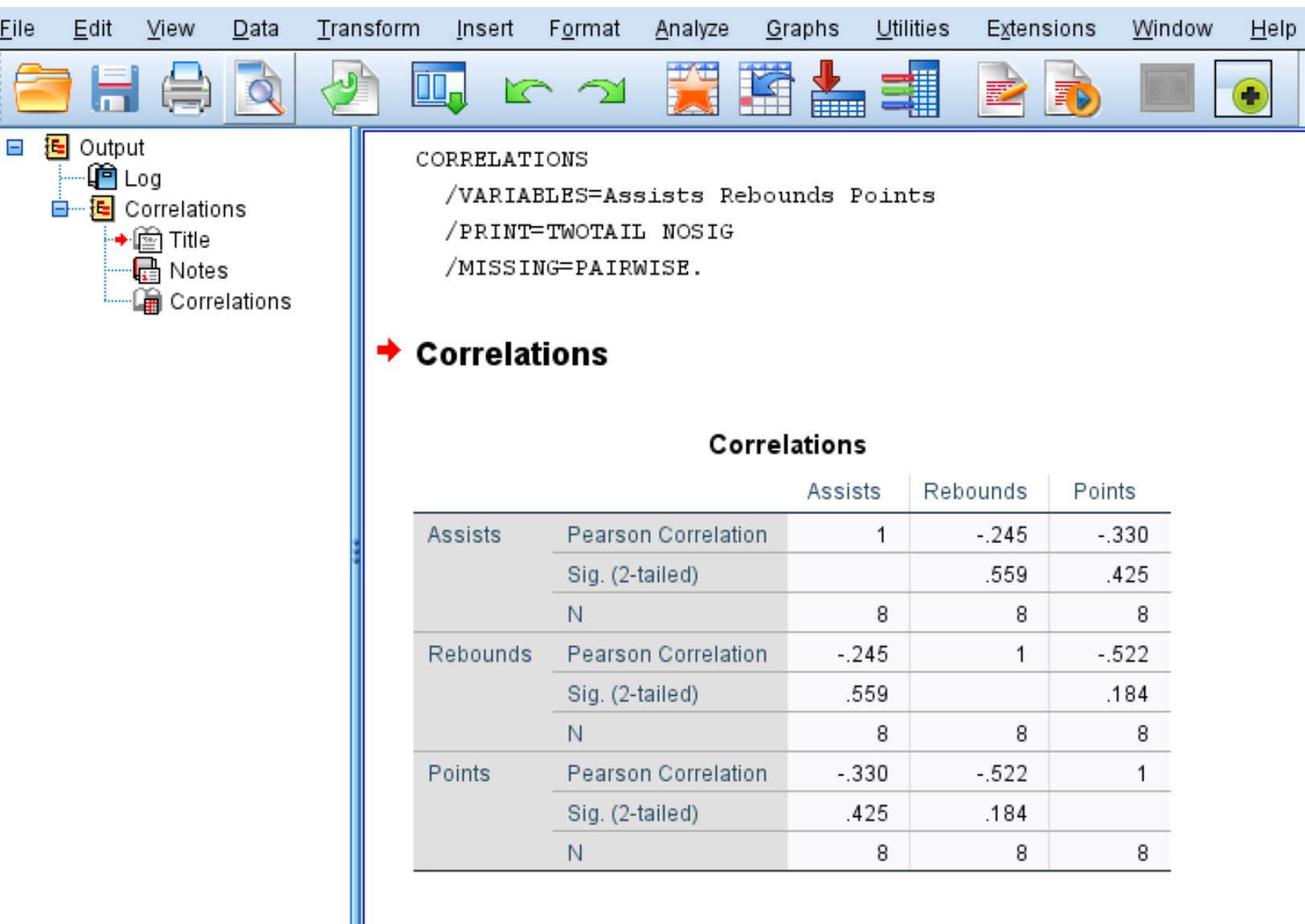
步骤 3：解释相关矩阵。

相关矩阵显示每个变量的以下三个测量值：

• 皮尔逊相关性：两个变量之间线性关联的度量，范围从 -1 到 1。
• 签名。 （双尾）：与相关系数相关的双尾 p 值。这告诉您两个变量是否具有统计显着关联（例如，如果 p < 0.05）
• N：用于计算皮尔逊相关系数的对数。

例如，以下是如何解释 Assists 变量的结果：

• 助攻和篮板之间的皮尔逊相关系数为-0.245 。由于这个数字是负数，这意味着这两个变量具有负相关性。
• 与助攻和篮板的 Pearson 相关系数相关的 p 值为0.559 。由于该值不小于 0.05，因此这两个变量不具有统计显着关联。
• 用于计算皮尔逊相关系数的对数为8 （例如，在该计算中使用了8对玩家）。

步骤 4：可视化相关矩阵。

您还可以创建散点图矩阵来可视化每个变量之间的线性关系。

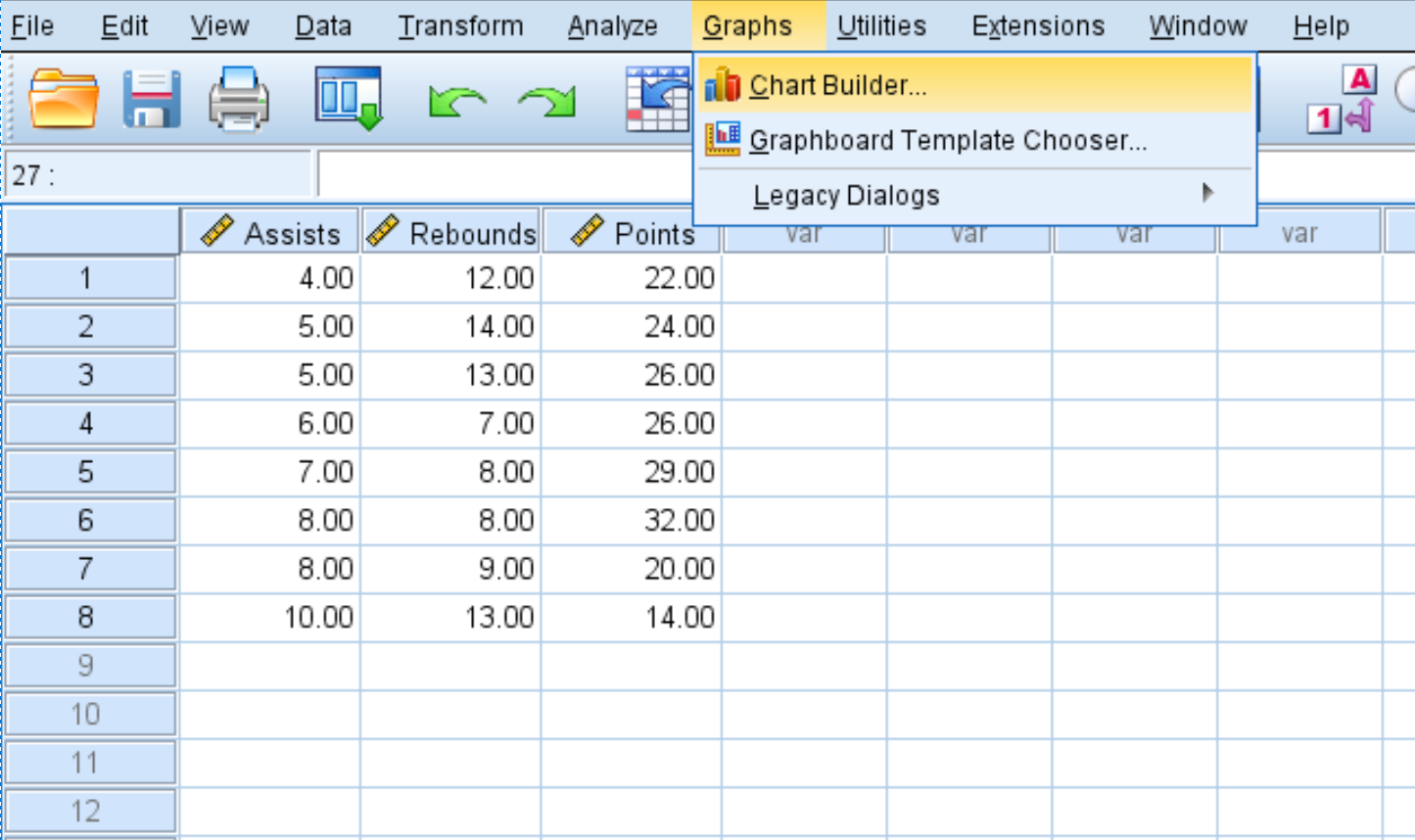
• 单击图表选项卡。
• 单击图表生成器。

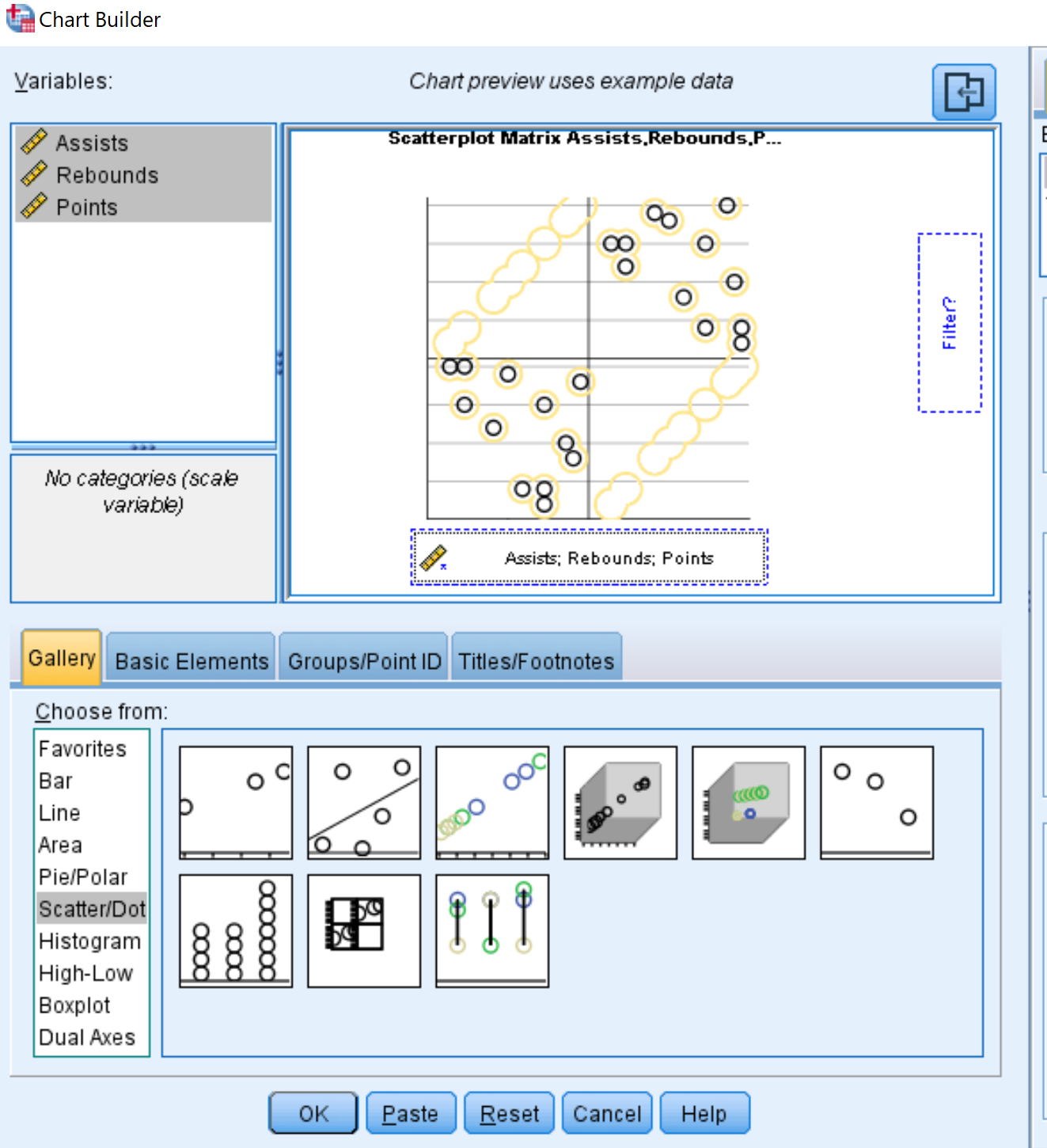
• 对于图表类型，单击散点/点。
• 单击显示Scatterplot Matrix的图像。
• 在左上角的“变量”框中，按住 Ctrl 并单击三个变量名称。将它们拖到图表底部显示Scattermatrix 的框。
• 最后，单击“确定” 。

将自动出现以下散点图矩阵：

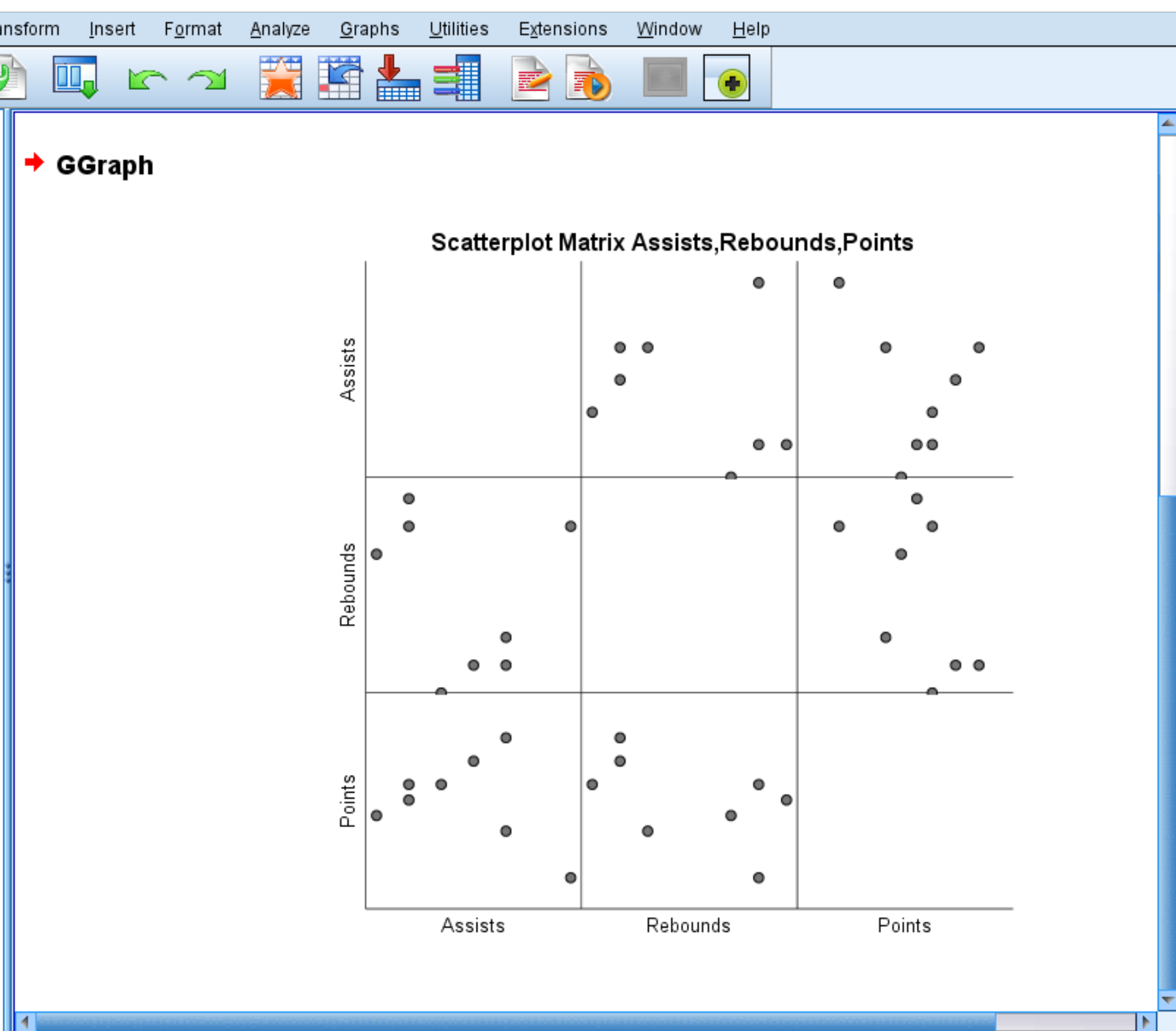
每个单独的散点图显示两个变量之间的成对组合。例如，左下角的散点图显示了数据集中 8 名球员的得分和助攻的成对组合。

散点图矩阵是可选的，但它提供了一种很好的方法来可视化数据集中变量的每个成对组合之间的关系。