如何在 spss 中检验正态性

许多统计测试要求一个或多个变量服从正态分布，测试结果才可靠。

本教程介绍了两种不同的方法，可用于在 SPSS 中测试变量的正态性。

每种方法都将使用以下数据集，该数据集显示 20 名不同篮球运动员每场比赛的平均得分：

方法一：直方图

查看变量是否服从正态分布的一种方法是创建直方图来显示变量的分布。如果变量呈正态分布，则直方图应呈“钟形”形状，靠近中心的值较多，位于尾部的值较少。

要为此篮球数据集创建直方图，我们可以单击“图表”选项卡，然后单击“图表生成器” 。

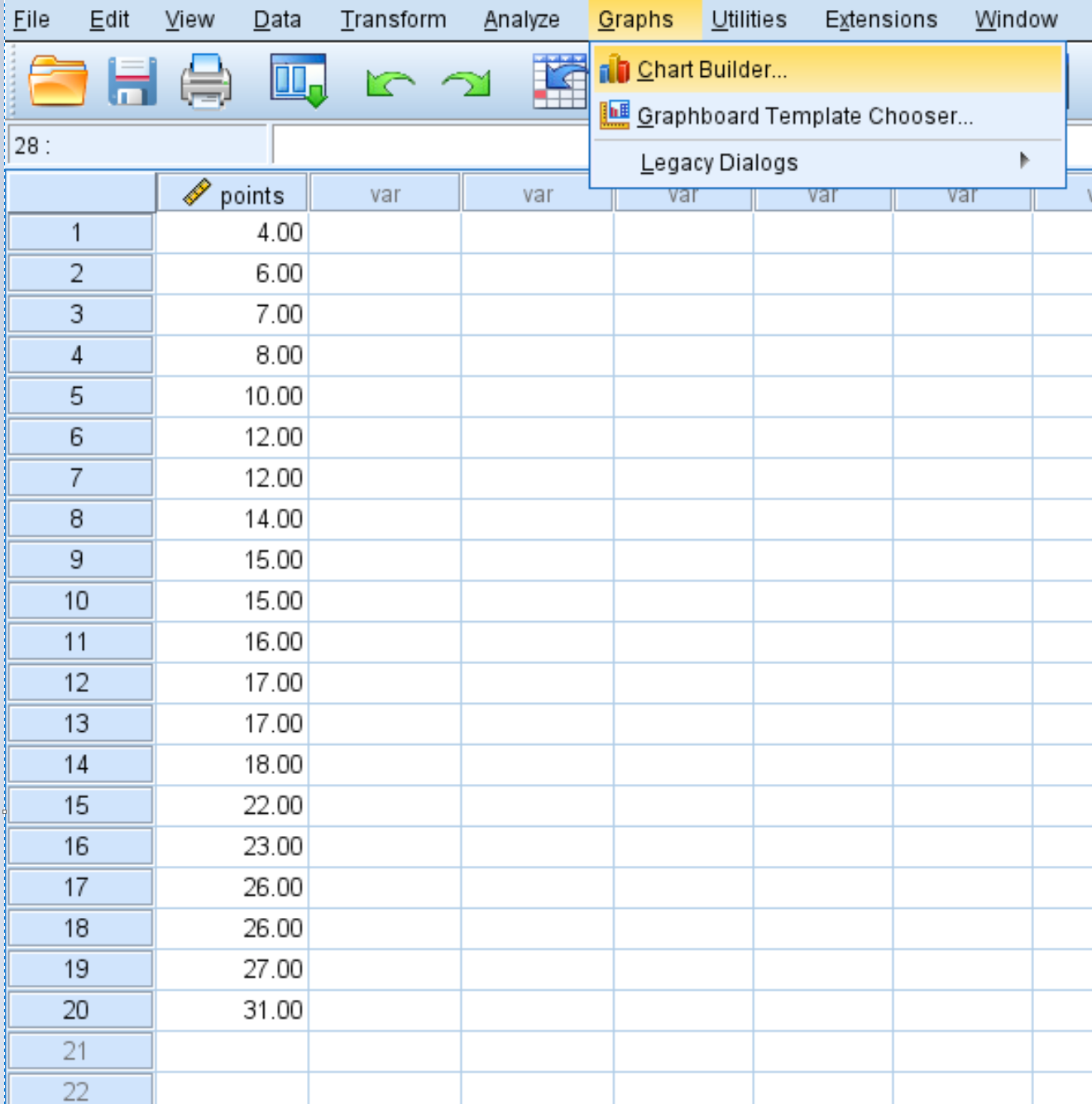
在出现的窗口中，从“选择范围”列表中选择“直方图”并将其拖到编辑窗口中。然后将变量点拖到 x 轴上：

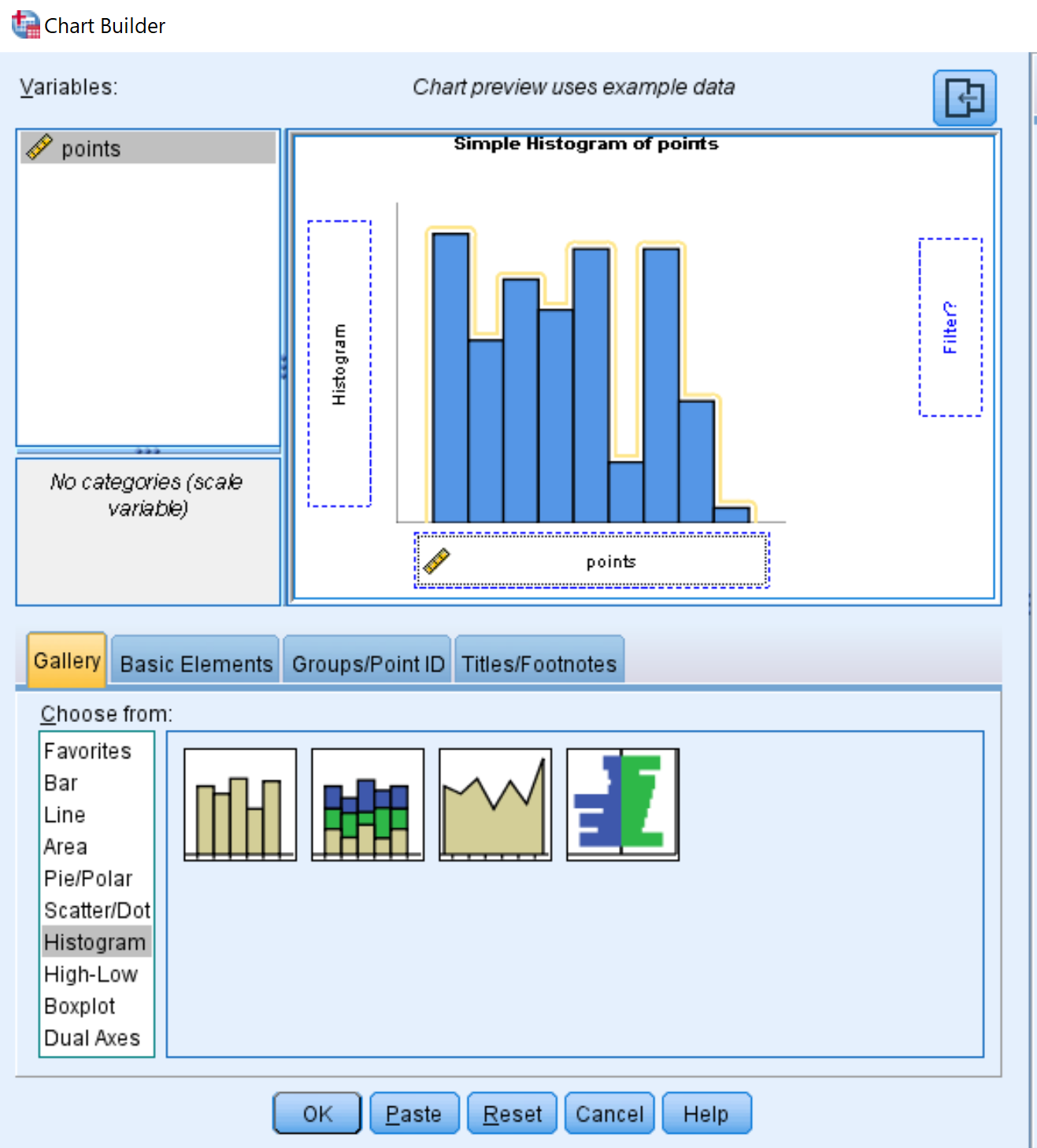
单击“确定”后，将出现以下直方图：

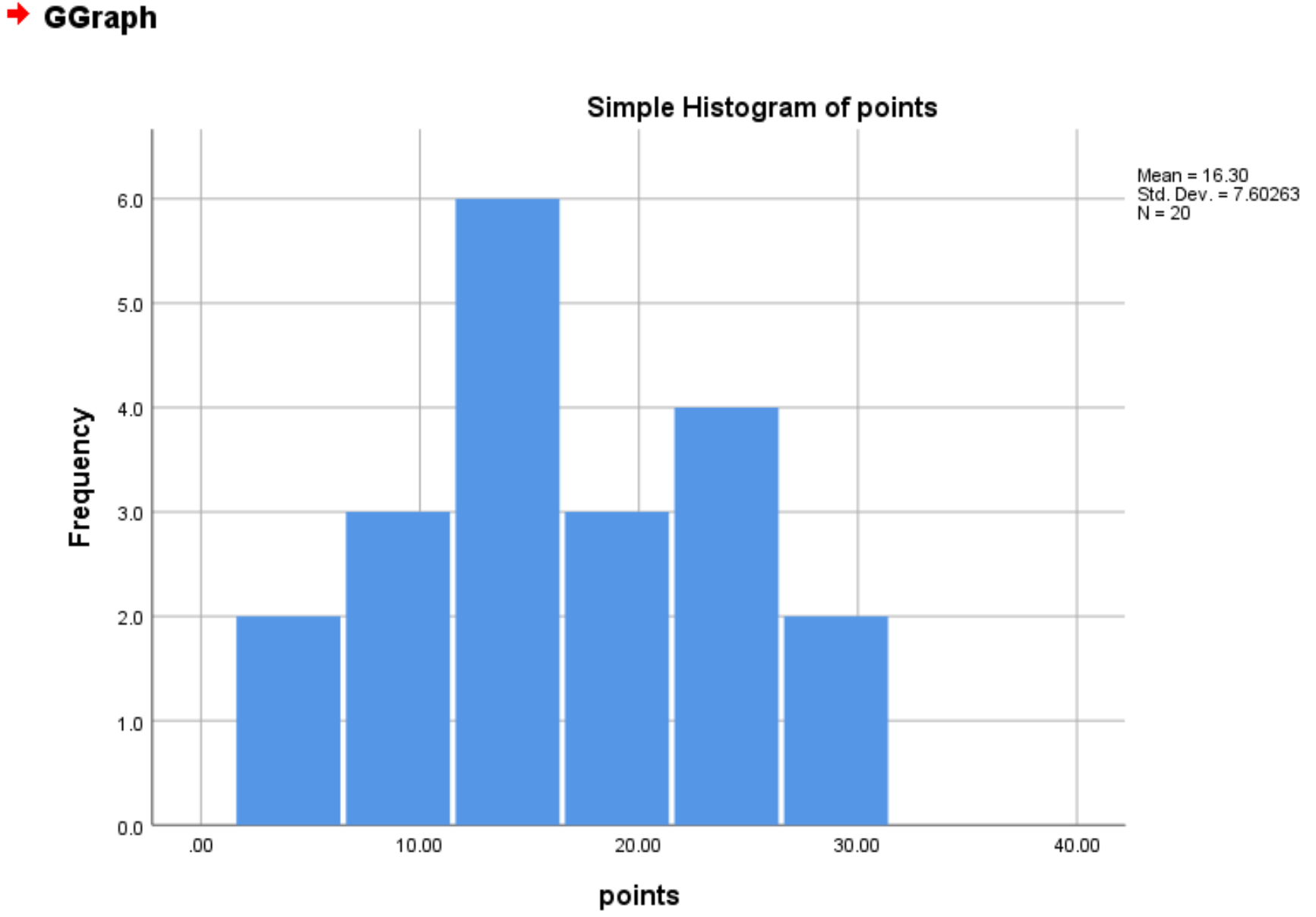
我们可以看到，变量分数并不是完全正态分布的，但它们大致呈钟形，大多数球员每场得分在 10 到 20 分之间，而得分超出该分数的球员则较少。

虽然这不是测试正态性的正式方法，但它为我们提供了一种快速可视化变量分布的方法，并让我们大致了解分布是否为钟形。

方法2：正式统计检验

我们还可以使用正式的统计检验来确定变量是否服从正态分布。 SPSS 提供以下正态性检验：

• 夏皮罗-威尔克检验
• 柯尔莫哥洛夫-斯米尔诺夫检验

每个检验的零假设是给定变量呈正态分布。如果检验的 p 值低于一定的显着性水平（常见选择包括 0.01、0.05 和 0.10），那么我们可以拒绝零假设并得出结论：有足够的证据断言变量不呈正态分布。

要在 SPSS 中同时执行这两个测试，请单击“分析”选项卡，然后单击“描述性统计” ，然后单击 探索：

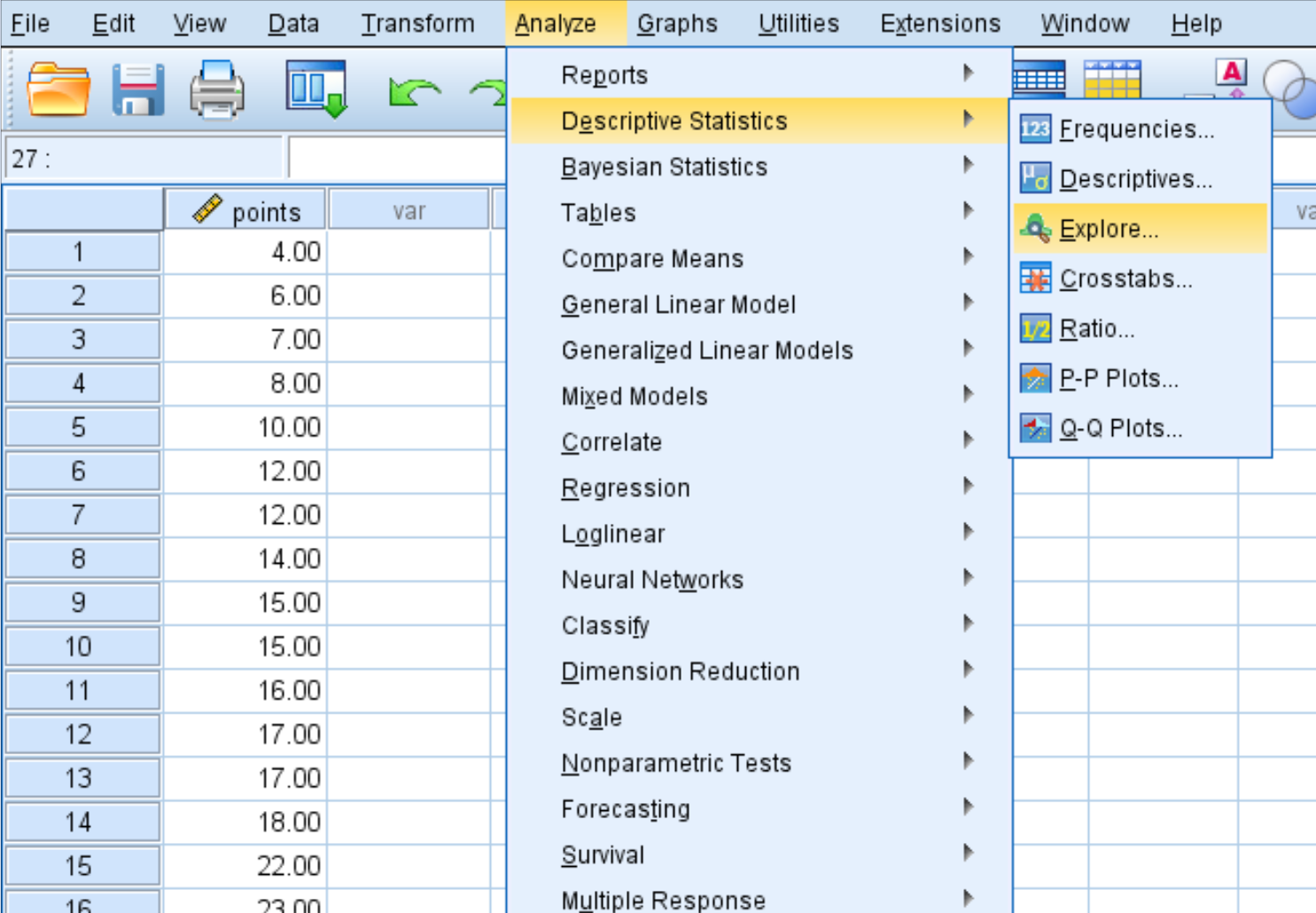
在出现的新窗口中，将变量点拖到标记为“从属列表”的区域中。然后单击“图”并确保选中“带检验的正态图”旁边的框。然后单击“继续” 。然后单击“确定” 。

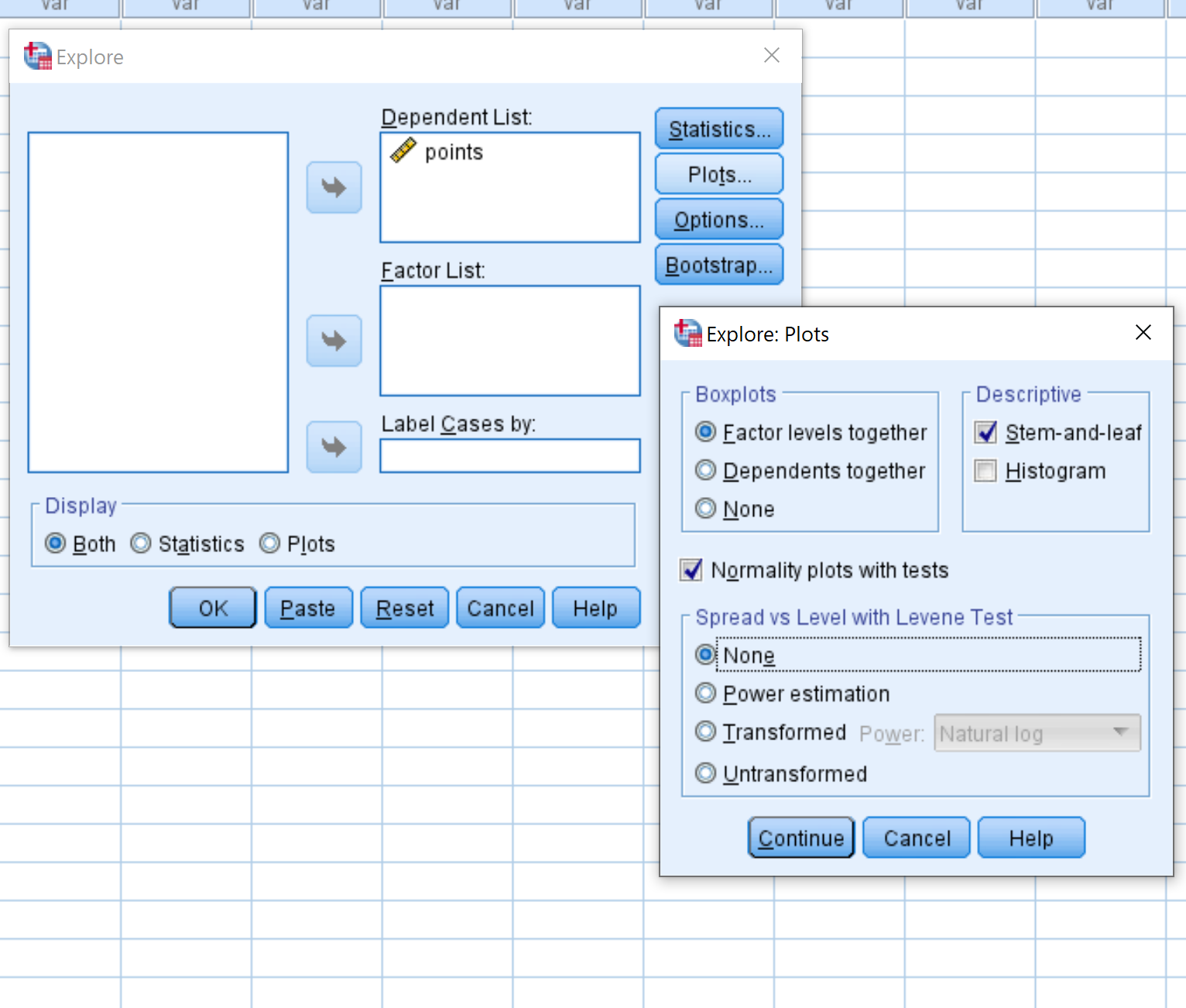
单击“确定”后，正态性检验结果将显示在以下框中：

显示每个测试的测试统计量和相应的 p 值：

柯尔莫哥洛夫-斯米尔诺夫检验：

• 检验统计量： 0.113
• p 值： 0.200

夏皮罗-威尔克检验：

• 检验统计量： 0.967
• p 值： 0.699

两项检验的 p 值均不小于 0.05，这意味着我们没有足够的证据表明point变量不呈正态分布。

如果我们想假设变量服从正态分布来进行统计检验，我们就会知道变量点满足这个假设。