如何在 spss 中进行简单线性回归
简单线性回归是我们可以用来理解预测变量和响应变量之间关系的方法。
本教程介绍如何在 SPSS 中执行简单线性回归。
示例：SPSS 中的简单线性回归
假设我们有以下数据集，显示 20 名学生的学习小时数和考试成绩：
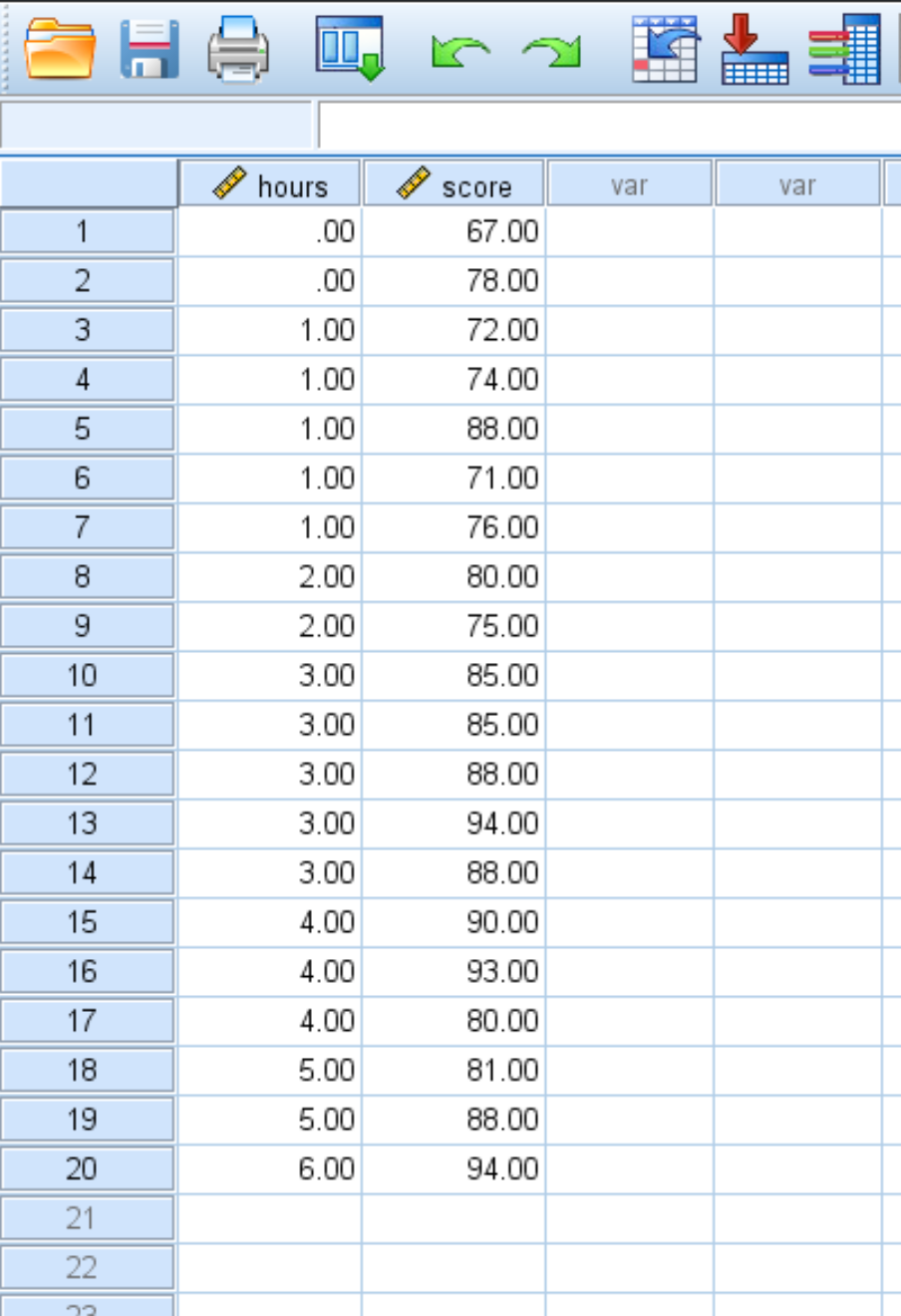
使用以下步骤对此数据集执行简单的线性回归，以量化学习时间和考试分数之间的关系：
步骤 1：可视化数据。
首先，我们将创建一个散点图来可视化小时数和分数之间的关系，以确保两个变量之间的关系看起来是线性的。否则，简单线性回归将不是一种合适的技术。
单击“图表”选项卡，然后单击“图表生成器” ：
从“选择来源”菜单中，单击散点/点并将其拖动到主编辑窗口中。然后将变量时间拖到 x 轴上，将分数拖到 y 轴上。
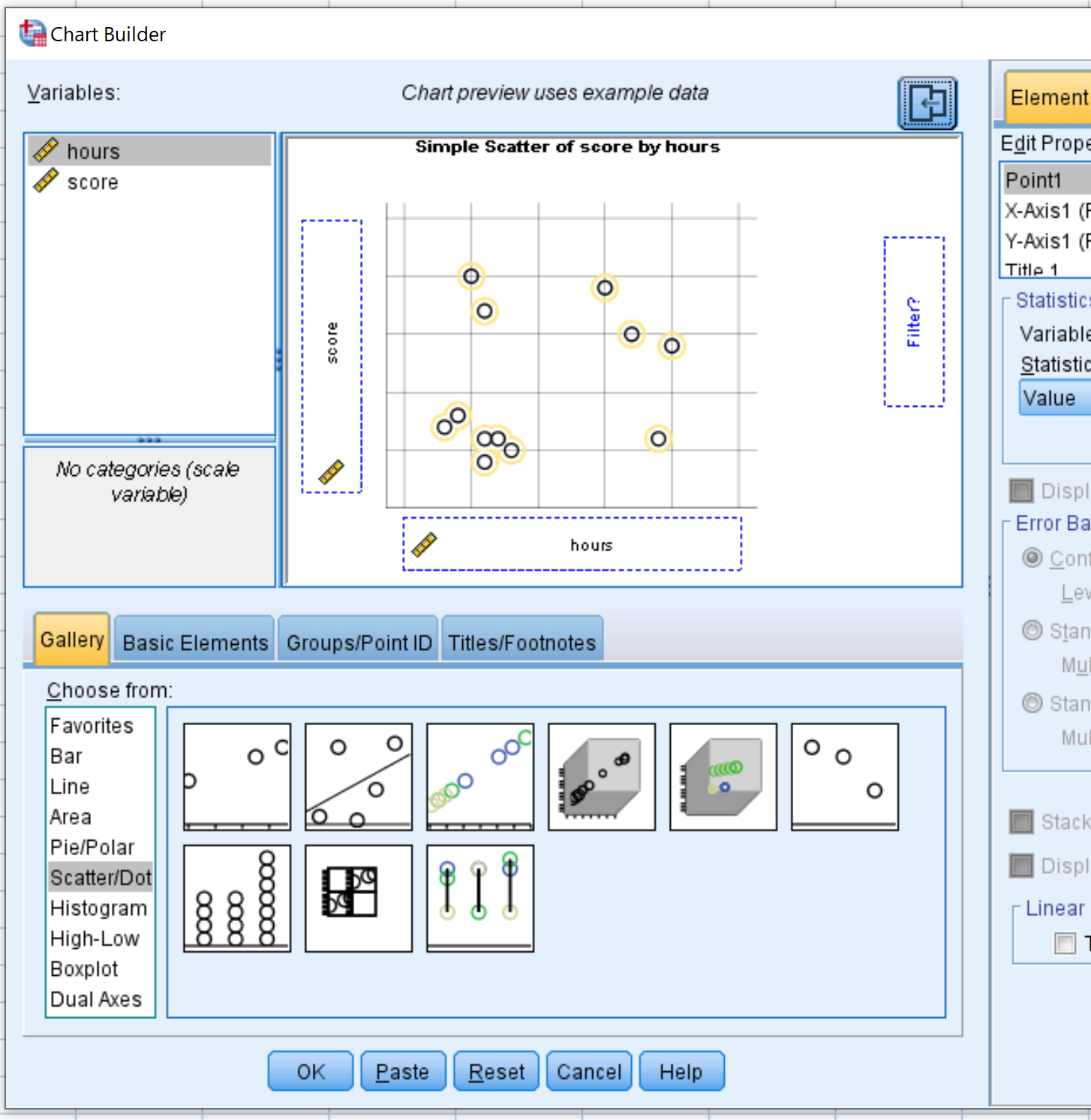
单击“确定”后，将出现以下散点图：
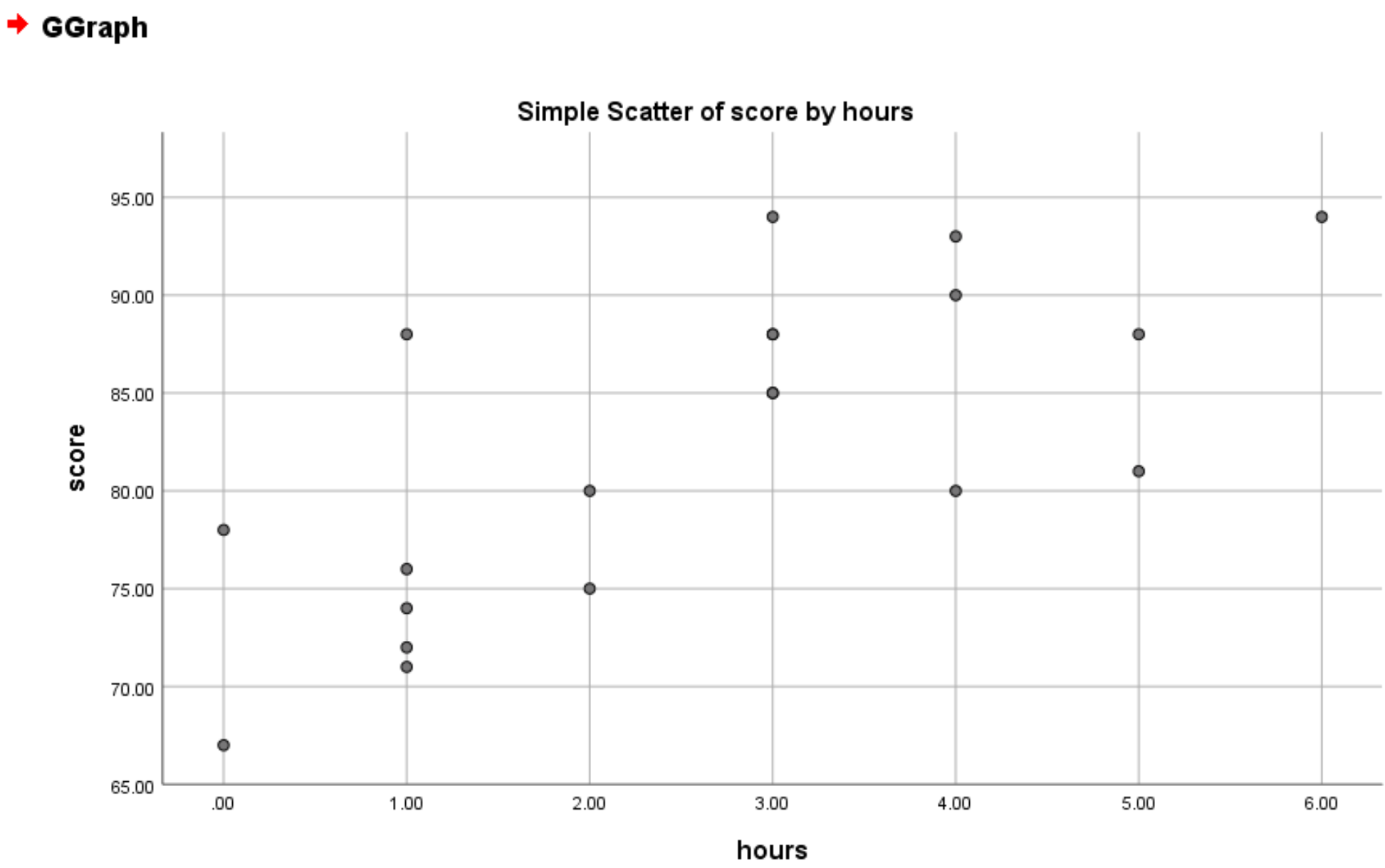
从图中我们可以看出，时间和成绩之间存在正线性关系。一般来说，学习时间越长的学生往往得分越高。
由于两个变量之间存在明显的线性关系，我们将继续对数据集拟合一个简单的线性回归模型。
步骤 2：拟合一个简单的线性回归模型。
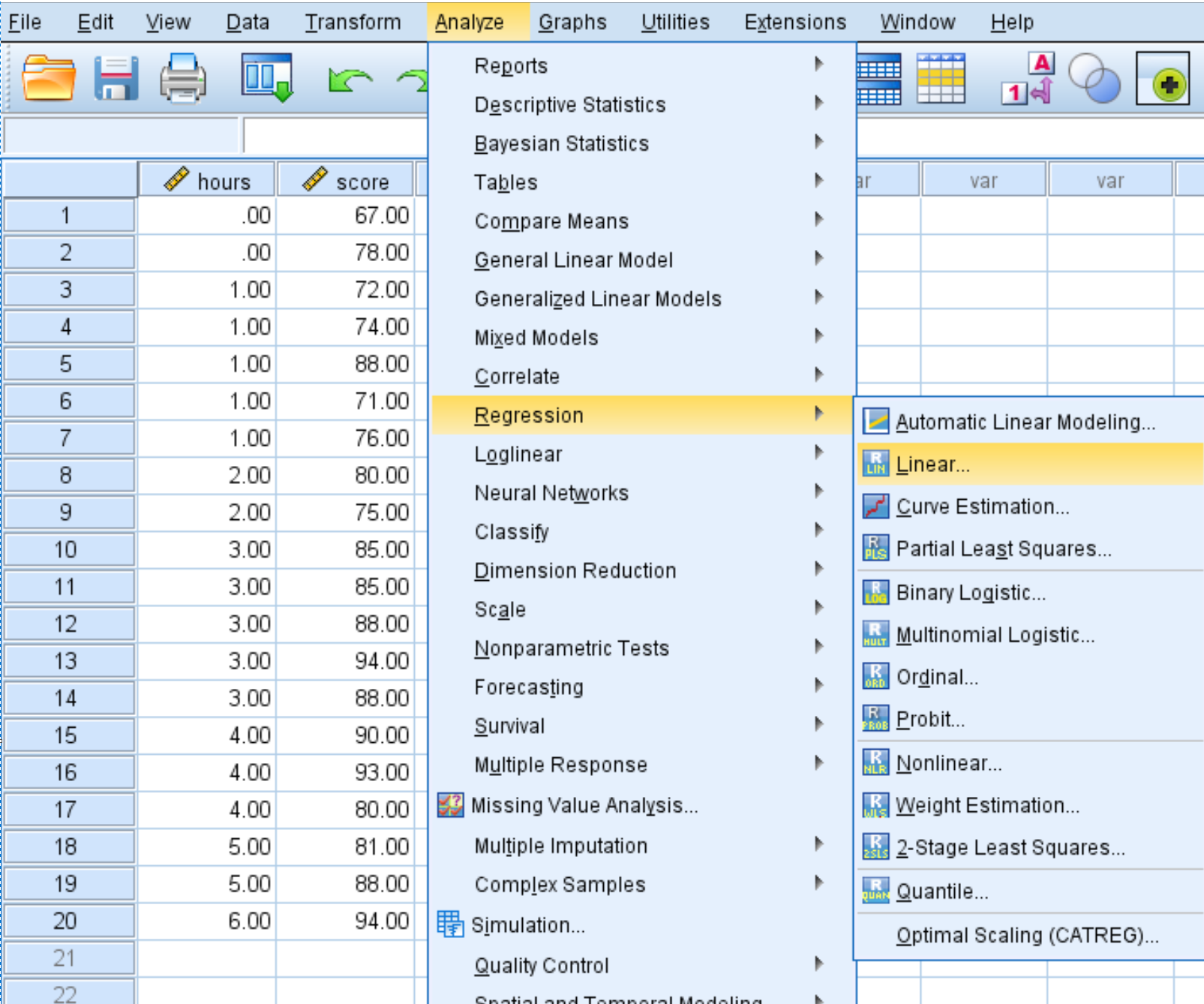
单击“分析”选项卡，然后单击“回归” ，然后单击“线性” ：
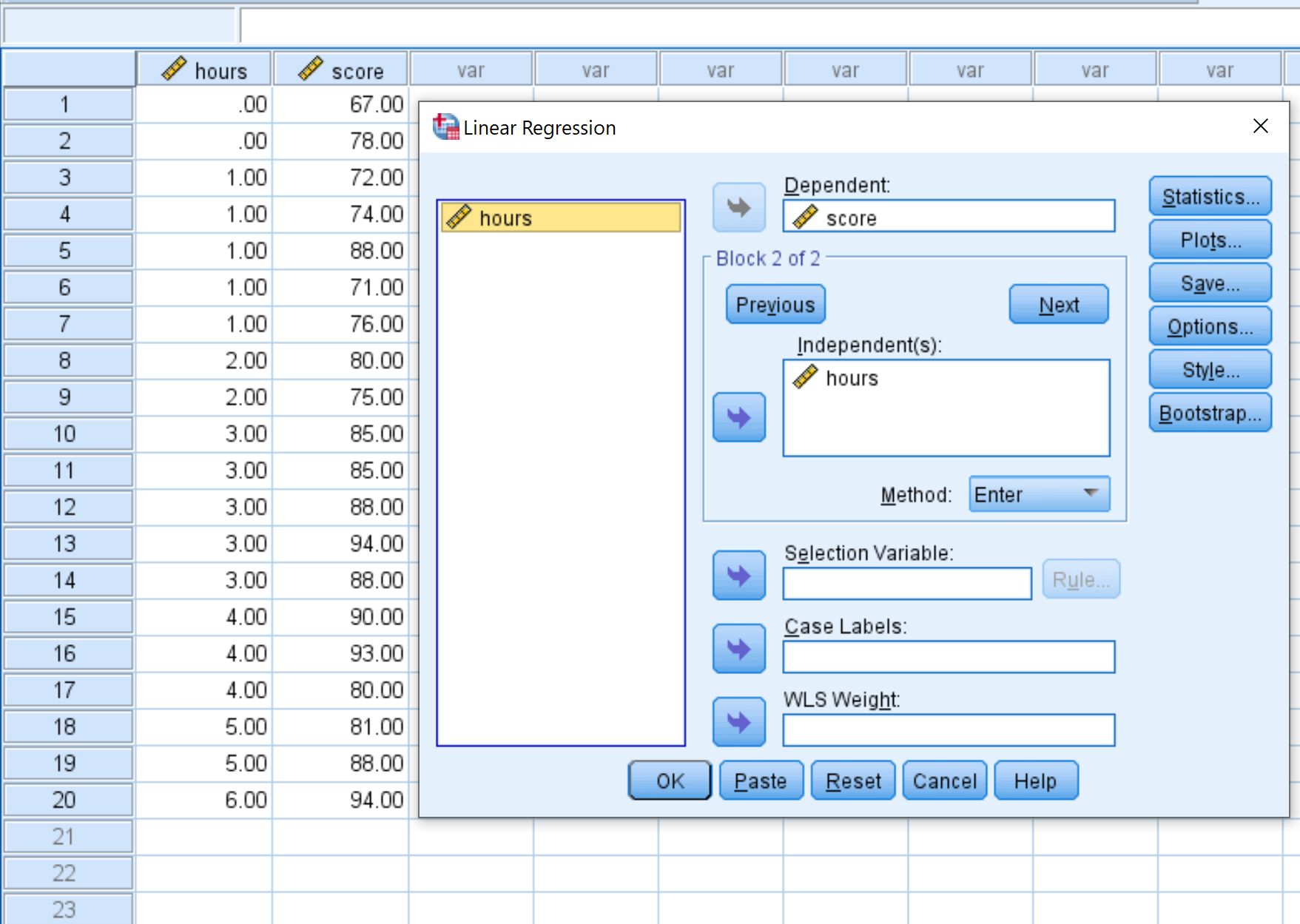
在出现的新窗口中，将变量分数拖动到标记为“从属”的框中，并将小时数拖动到标记为“独立”的框中。然后单击“确定” 。
第 3 步：解释结果。
单击“确定”后，将显示简单线性回归结果。我们感兴趣的第一个表是名为“模型摘要”的表：
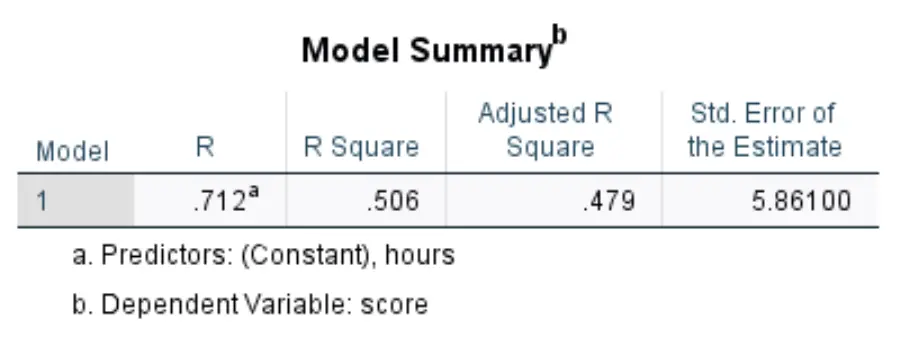
以下是如何解释此表中最相关的数字：
- R 方：这是可以由解释变量解释的响应变量中方差的比例。在此示例中， 50.6%的考试成绩差异可以通过学习时间来解释。
- 标准。估计误差：标准误差是观测值与回归线之间的平均距离。在此示例中，观测值与回归线平均偏差5,861个单位。
我们感兴趣的下表的标题是“系数” ：
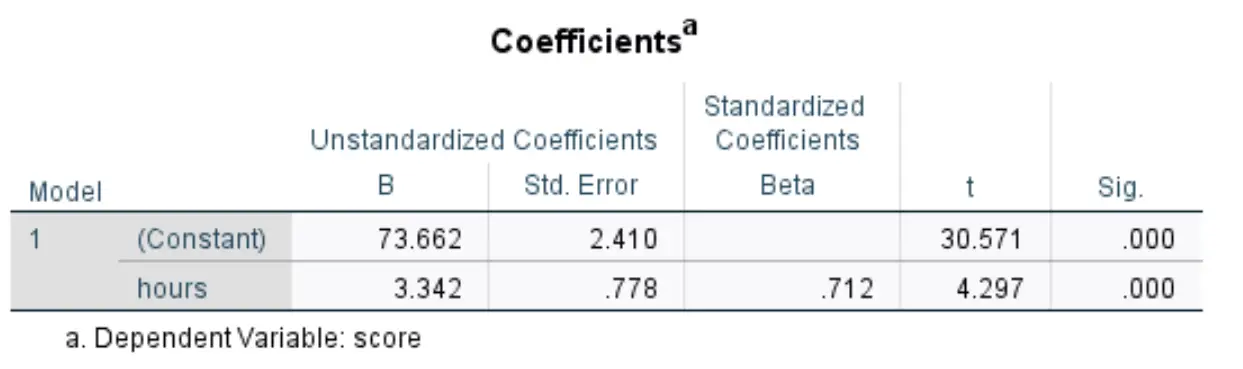
以下是如何解释此表中最相关的数字：
- 非标准化 B（常数） ：这告诉我们当预测变量为零时响应变量的平均值。在此示例中，当学习时间为零时，平均考试成绩为73.662 。
- B 非标准化（小时）：这告诉我们与预测变量增加一个单位相关的响应变量的平均变化。在此示例中，每多学习一小时，考试成绩平均就会增加3,342 。
- Sig（小时）：这是与小时内检验统计量相关的p 值。在本例中，由于该值小于 0.05，因此我们可以得出结论，预测变量hours具有统计显着性。
最后，我们可以使用constant和hours的值形成回归方程。在这种情况下，方程为：
预计考试成绩 = 73.662 + 3.342*（小时）
我们可以使用这个方程根据学习的小时数找到学生的估计考试成绩。
例如，学习 3 小时的学生应获得 83.688 的考试成绩：
预计考试成绩 = 73.662 + 3.342*(3) = 83.688
第四步：报告结果。
最后，我们想总结一下简单线性回归的结果。以下是如何执行此操作的示例：
进行简单的线性回归来量化学习时间和考试成绩之间的关系。分析中使用了 20 名学生的样本。
结果显示，学习时间和考试成绩之间存在统计显着关系（t = 4.297，p < 0.000），并且学习时间占考试成绩解释变异的 50.6%。考试。
回归方程为：
预计考试成绩 = 73.662 + 3.342*（小时）
平均每多学习一小时，考试成绩就会提高3,342分。
其他资源
以下教程说明如何在 SPSS 中执行其他常见任务：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多