如何在 spss 中执行双向方差分析

双向方差分析用于确定已分成两个因素的三个或更多独立组的平均值之间是否存在统计显着差异。

双向方差分析的目的是确定两个因素对响应变量的影响，并确定这两个因素对响应变量是否存在交互作用。

本教程介绍如何在 SPSS 中执行双向方差分析。

示例：SPSS 中的双向方差分析

植物学家想知道植物生长是否受到阳光照射和浇水频率的影响。她种下了 30 颗种子，让它们在不同的阳光照射和浇水频率条件下生长两个月。两个月后，她记录了每株植物的高度（以英寸为单位）。

结果如下所示：

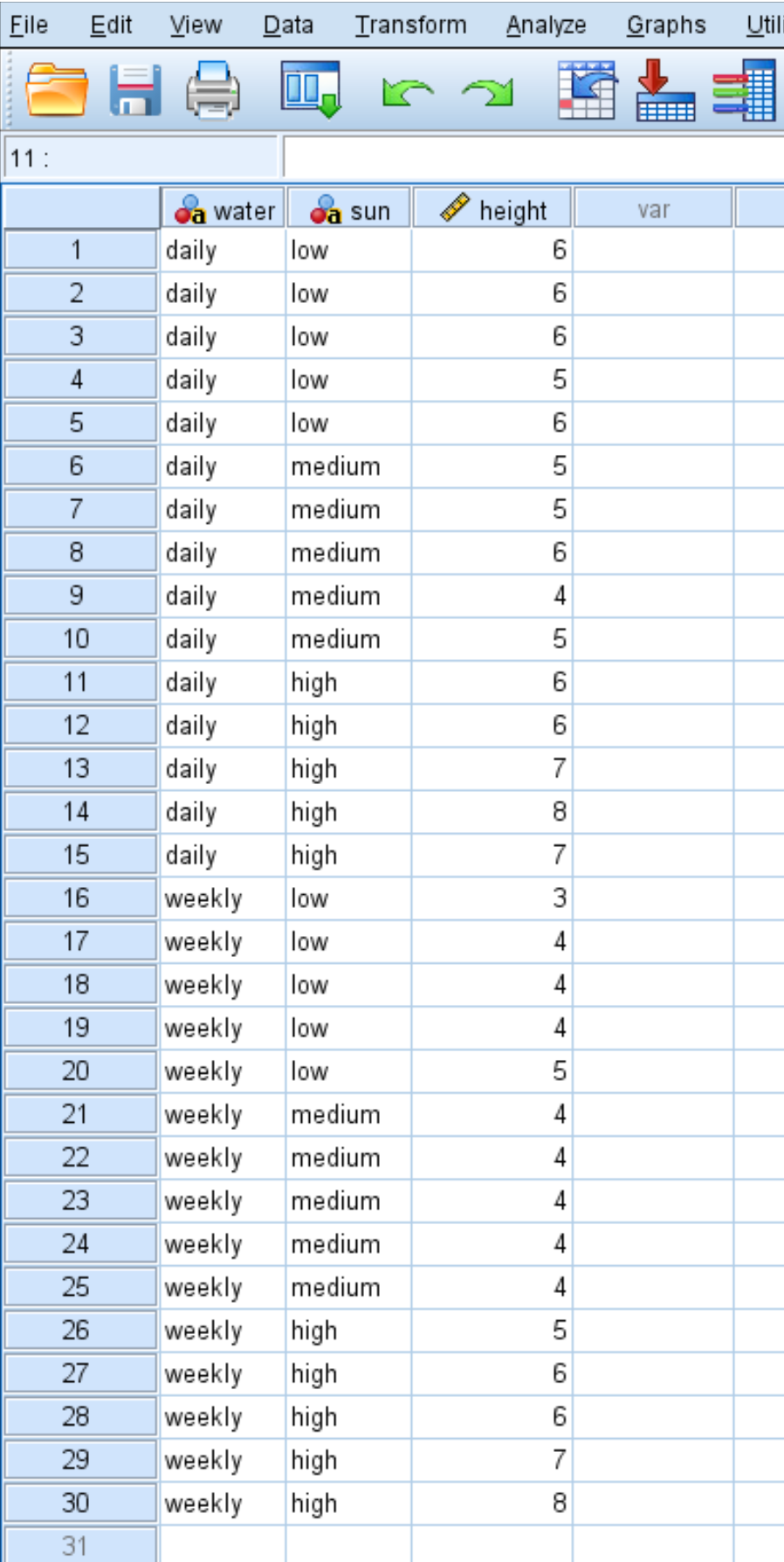
使用以下步骤进行双向方差分析，以确定浇水频率和阳光照射是否对植物生长有显着影响，并确定浇水频率和阳光照射之间是否存在交互作用。浇水和暴露在阳光下。

步骤 1：执行双向方差分析。

单击“分析”选项卡，然后单击“一般线性模型” ，然后单击“单变量” ：

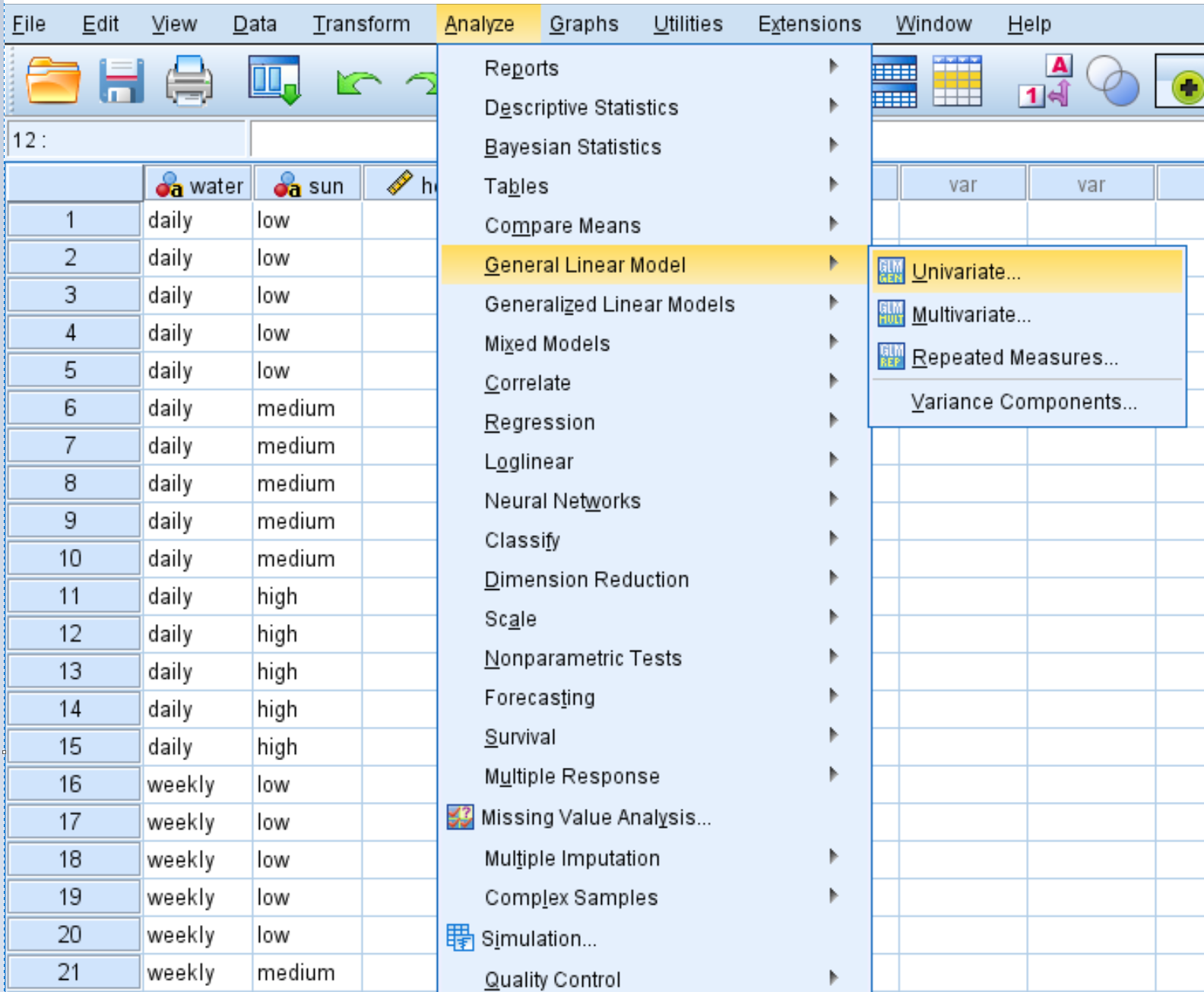
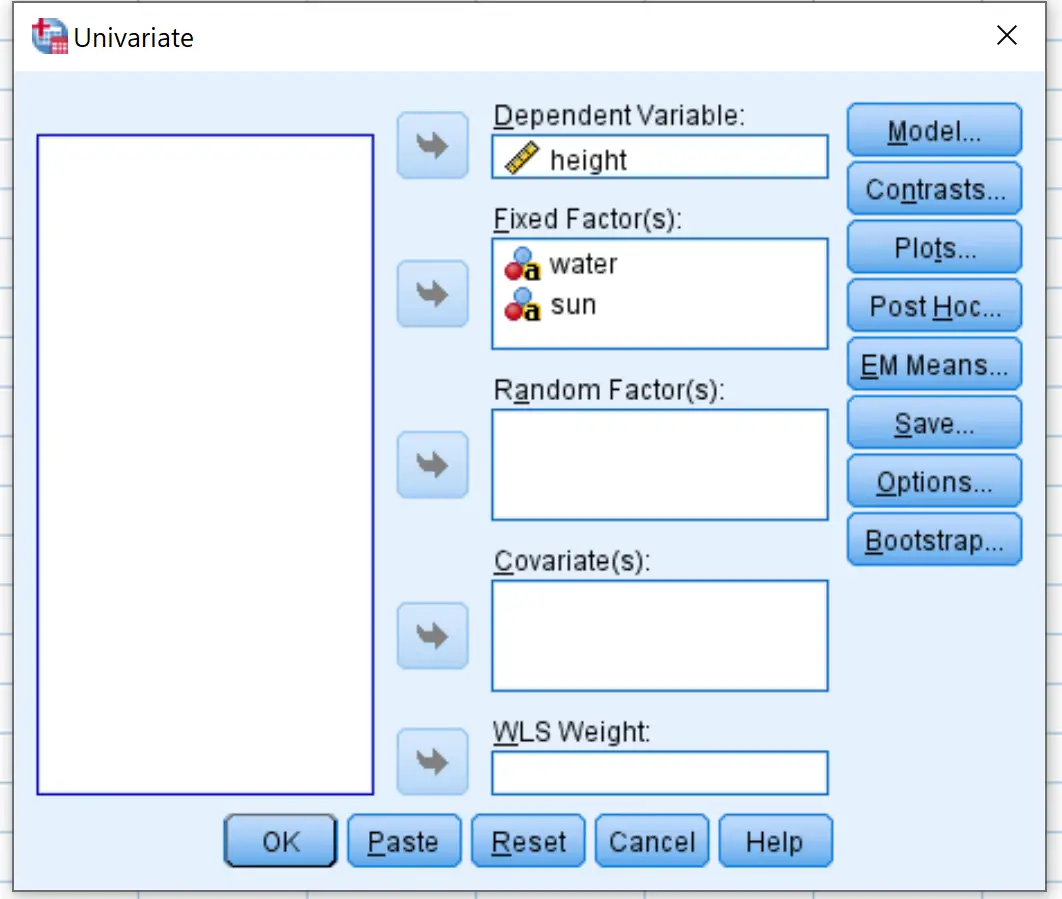
将响应变量的高度拖到标记为“因变量”的框中。将两个水和阳光因子变量拖到标记为“固定因子”的框中：

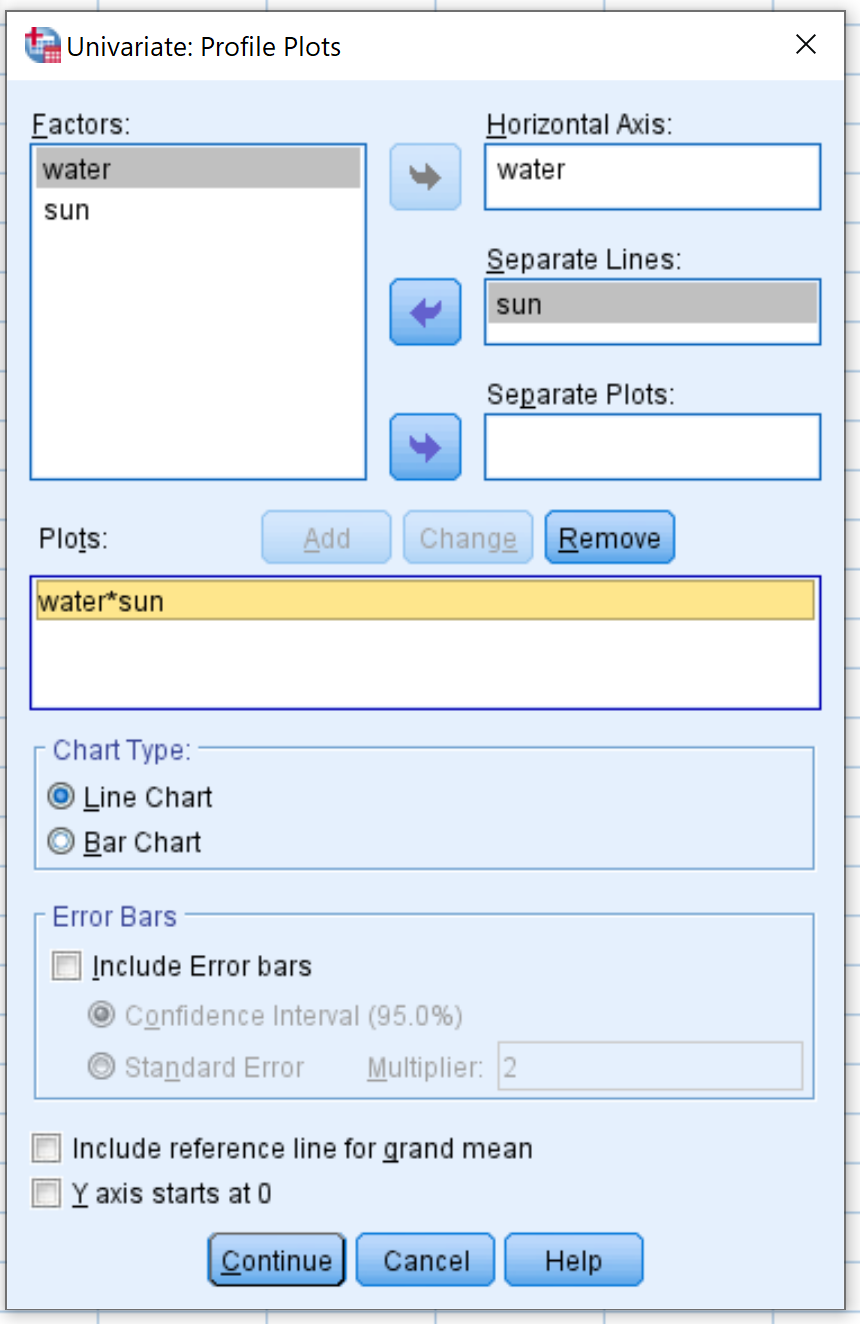
接下来，单击绘图按钮。将水拖入标记为“水平轴”的区域，将太阳拖入标记为“分隔线”的区域。然后单击“添加” 。 “水*太阳”一词将出现在标题为“绘图”的框中。然后单击“继续” 。

接下来，单击事后按钮。在出现的新窗口中，将sun变量拖到标记为事后测试的框中。然后选中Tukey旁边的框。然后单击“继续” 。

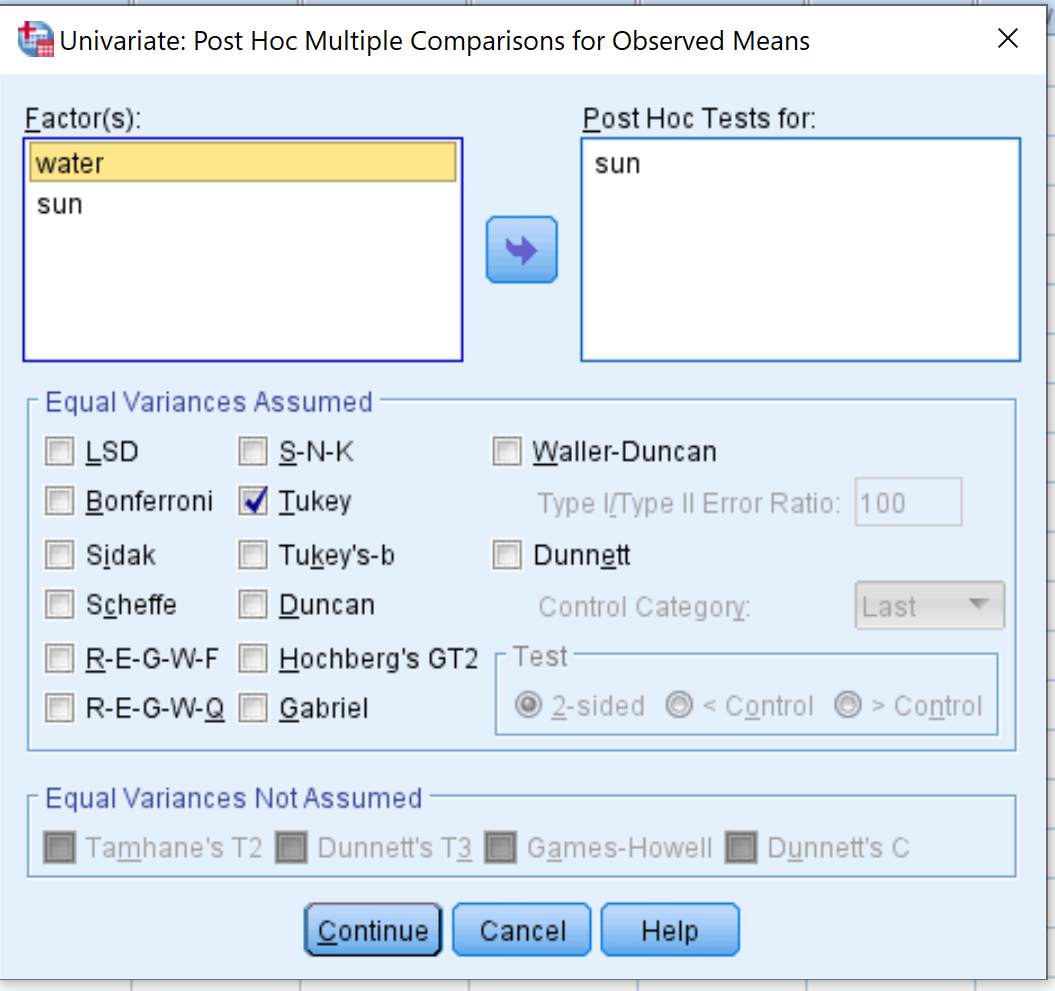
接下来，单击“EM 均值”按钮。将以下变量拖到标记为“显示平均值”的框中。然后单击“继续” 。

最后，单击“确定” 。

第 2 步：解释结果。

单击“确定”后，将显示双向方差分析结果。以下是如何解释结果：

受试者间效应测试

第一个表显示了水和阳光因素的 p 值，以及水*阳光的相互作用效应：

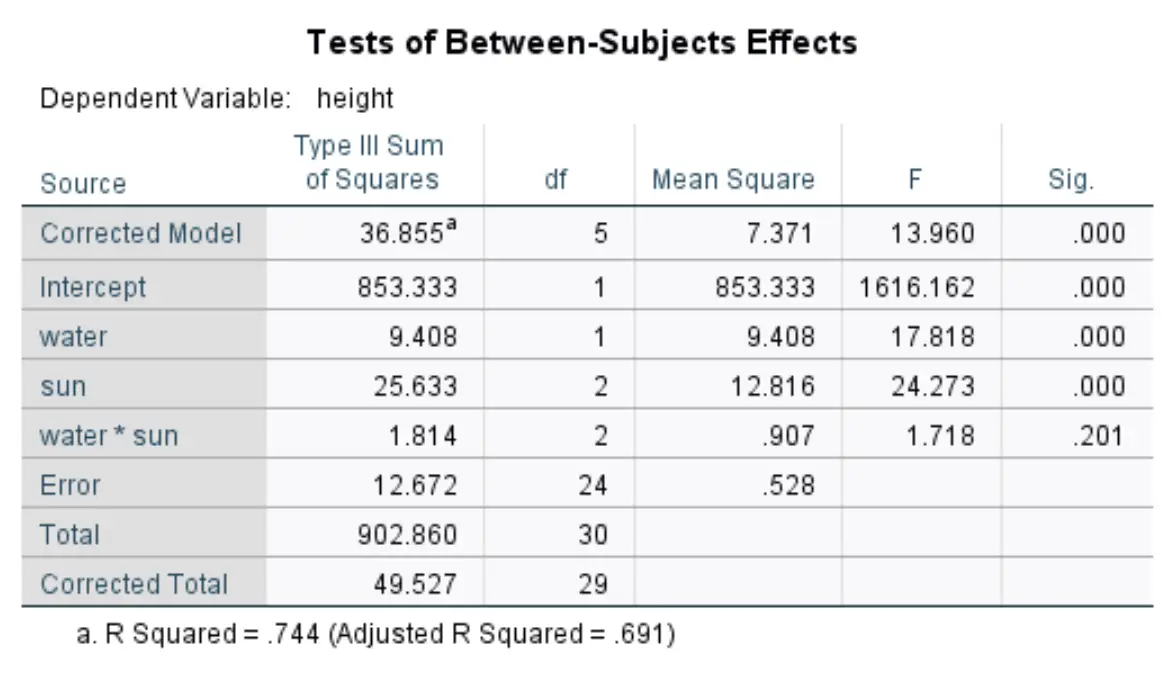
我们可以看到表中每个因素的以下 p 值：

• 水： p 值 = 0.000
• 太阳： p 值 = 0.000
• 水*阳光： p 值 = 0.201

由于水和阳光的 p 值小于 0.05，这告诉我们这两个因素对植物高度具有统计上显着的影响。

由于交互效应的 p 值 (0.201) 不小于 0.05，这告诉我们阳光照射和浇水频率之间不存在显着的交互效应。

估计边际均值

第一个表显示每个因素的观测值平均值：

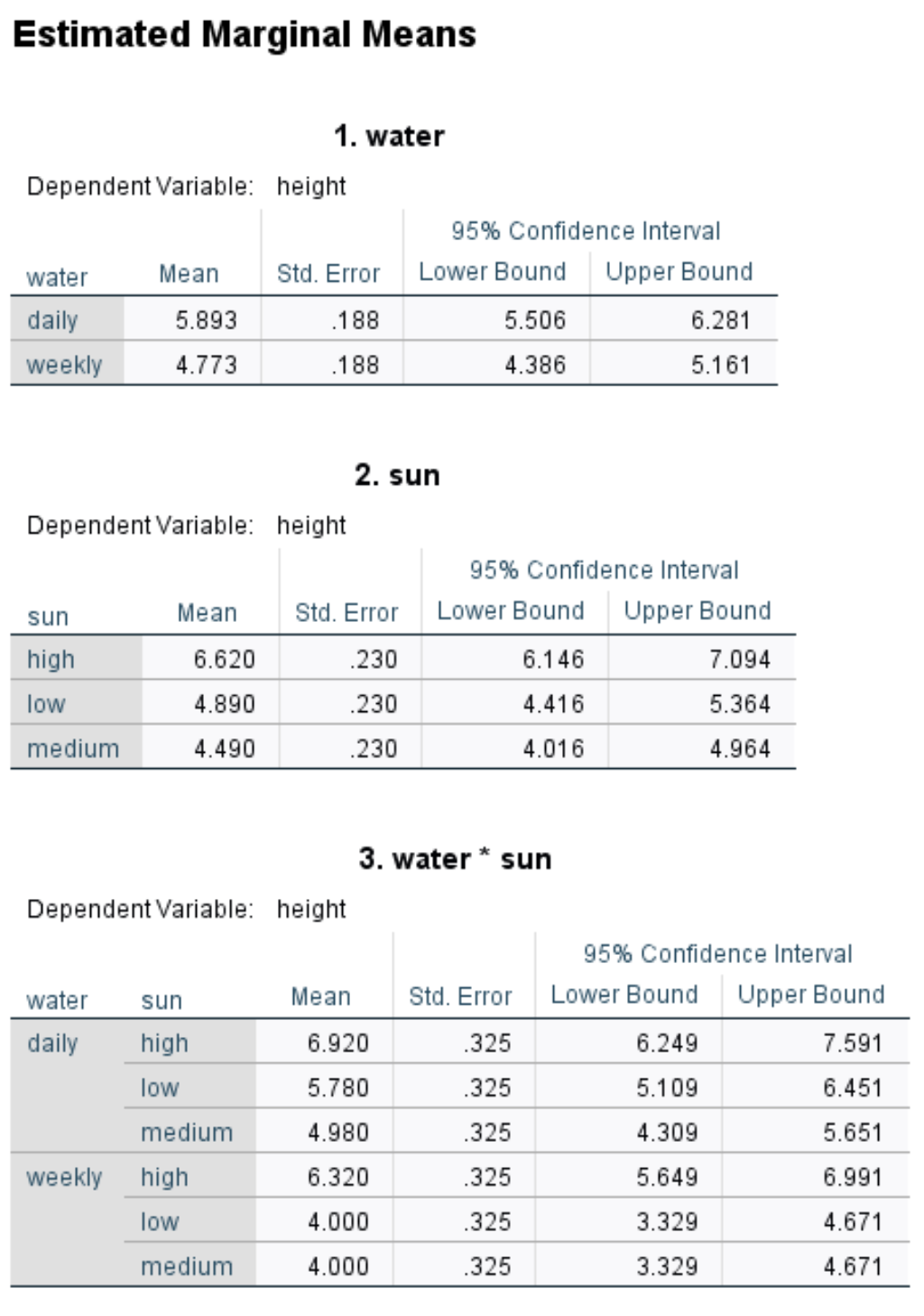
例如：

• 每天浇水的植物的平均高度为5.893英寸。
• 强烈阳光照射下植物的平均高度为6.62英寸。
• 每天浇水并大量暴露在阳光下的植物的平均高度为6.32英寸。

等等。

事后测试

该表显示了 Tukey 对三种不同阳光照射水平之间的事后比较的 p 值。

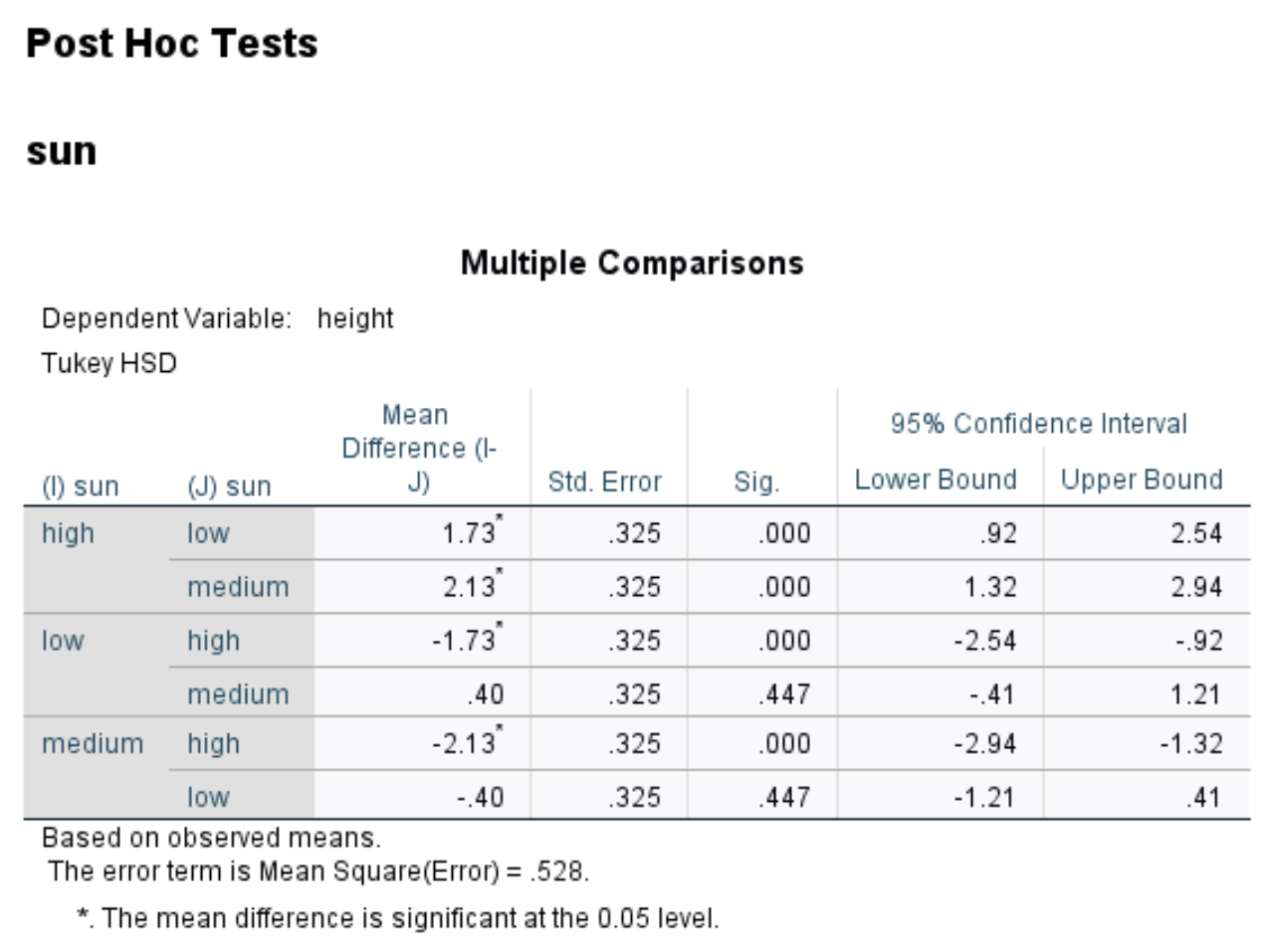
在表中我们可以看到以下比较的 p 值：

• 高 vs.低: | p 值 = 0.000
• 高与中| p 值 = 0.000
• 低与中| p 值 = 0.447

这告诉我们，高和低阳光照射之间以及高和中阳光照射之间存在统计显着差异，但低和中阳光照射之间没有显着差异。

第三步：报告结果。

最后，我们可以报告双向方差分析的结果。以下是如何执行此操作的示例：

进行双向方差分析以确定浇水频率（每天或每周）和阳光照射（低、中、高）是否对植物生长有显着影响。研究中总共使用了 30 种植物。

双向方差分析显示浇水频率 (p < 0.000) 和阳光照射 (p < 0.000) 均对植物生长具有统计显着影响。

每天浇水的植物比每周浇水的植物生长明显更快。

此外，图基的多重比较测试表明，接受高日照照射的植物比接受中度或低日照照射的植物生长显着更高。然而，接受中度和低度阳光照射的植物之间没有显着差异。

浇水频率和阳光照射之间也没有统计学上显着的交互作用。