如何在 spss 中创建和解释 roc 曲线

逻辑回归是一种统计方法，当响应变量是二元时，我们用它来拟合回归模型。为了评估逻辑回归模型对数据集的拟合程度，我们可以查看以下两个指标：

• 敏感性：当结果实际上是积极的时，模型预测观察结果为积极的概率。
• 特异性：当结果实际上为负时，模型预测观察结果为负的概率。

可视化这两个指标的一个简单方法是创建ROC 曲线，它是显示逻辑回归模型的敏感性和特异性的图表。

本教程介绍如何在 SPSS 中创建和解释 ROC 曲线。

示例：SPSS 中的 ROC 曲线

假设我们有以下数据集，显示一名篮球运动员是否被选入 NBA（0 = 否，1 = 是）以及他在大学期间的场均得分：

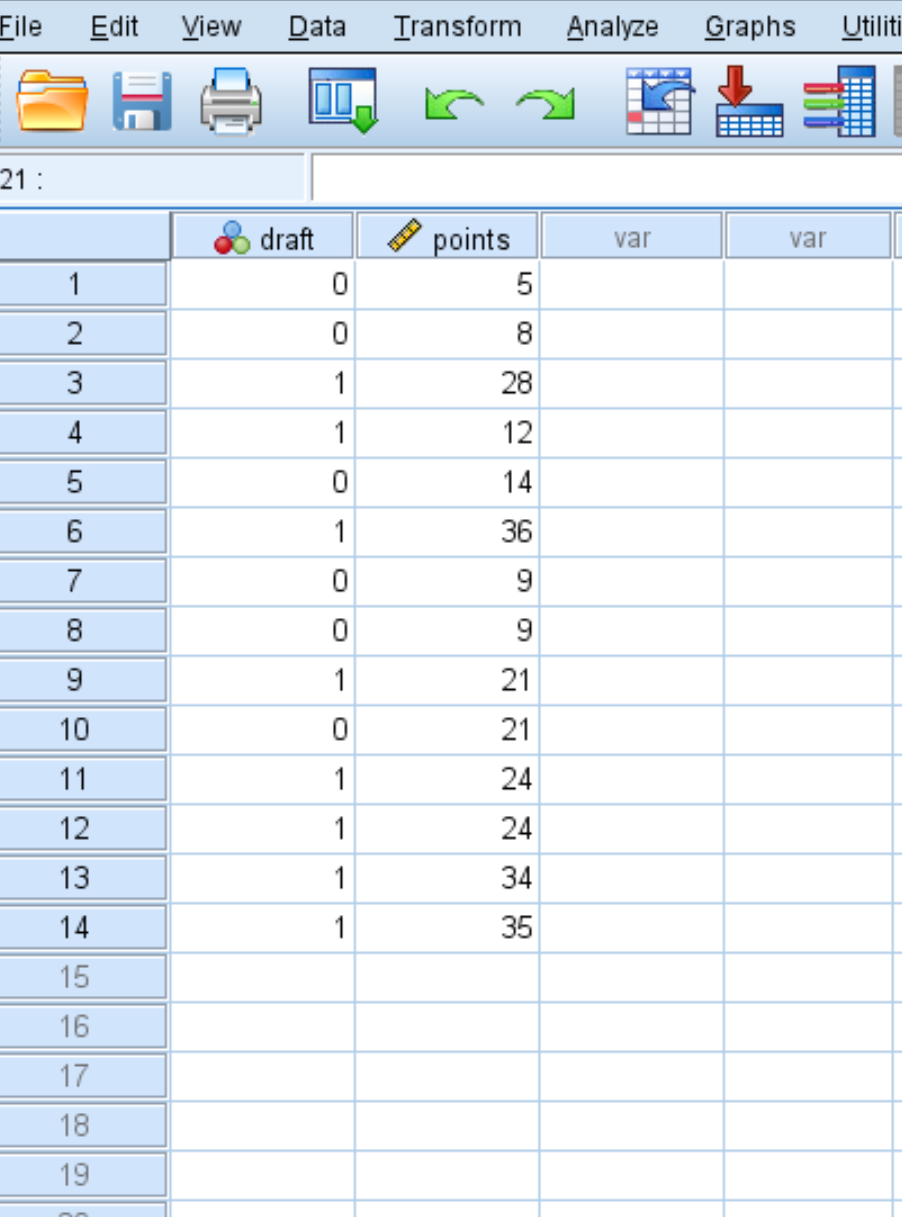
要为此数据集创建 ROC 曲线，请单击“分析”选项卡，然后单击“分类” ，然后单击“ROC 曲线” ：

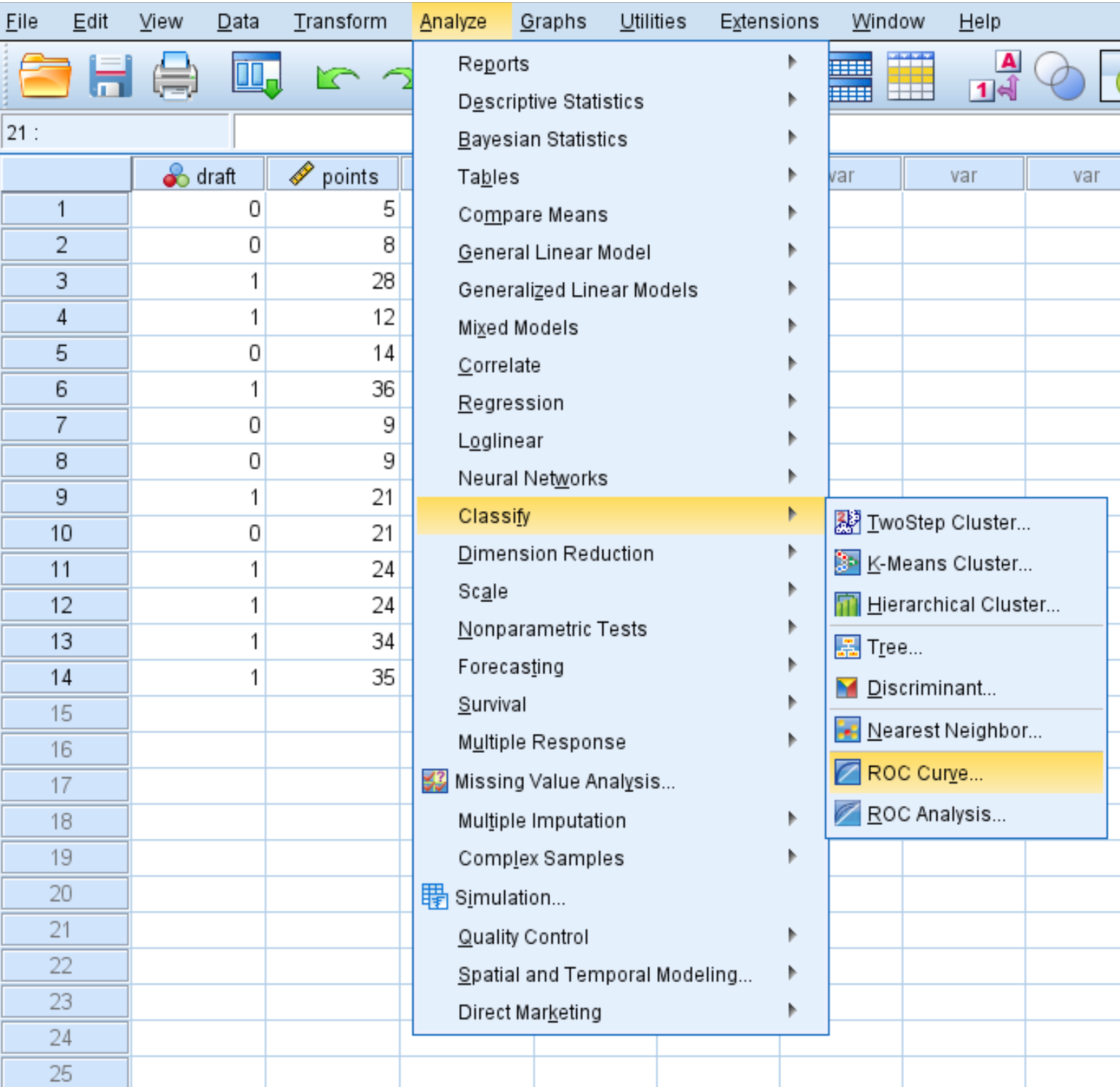
在出现的新窗口中，将草图变量拖到标记为“状态变量”的区域中。将状态变量的值设置为1 。 （该值表示球员已被选中）。将变量点拖到标记为“测试变量”的区域中。

选中“使用对角参考线”和“ROC 曲线点坐标”旁边的框。然后单击“确定” 。

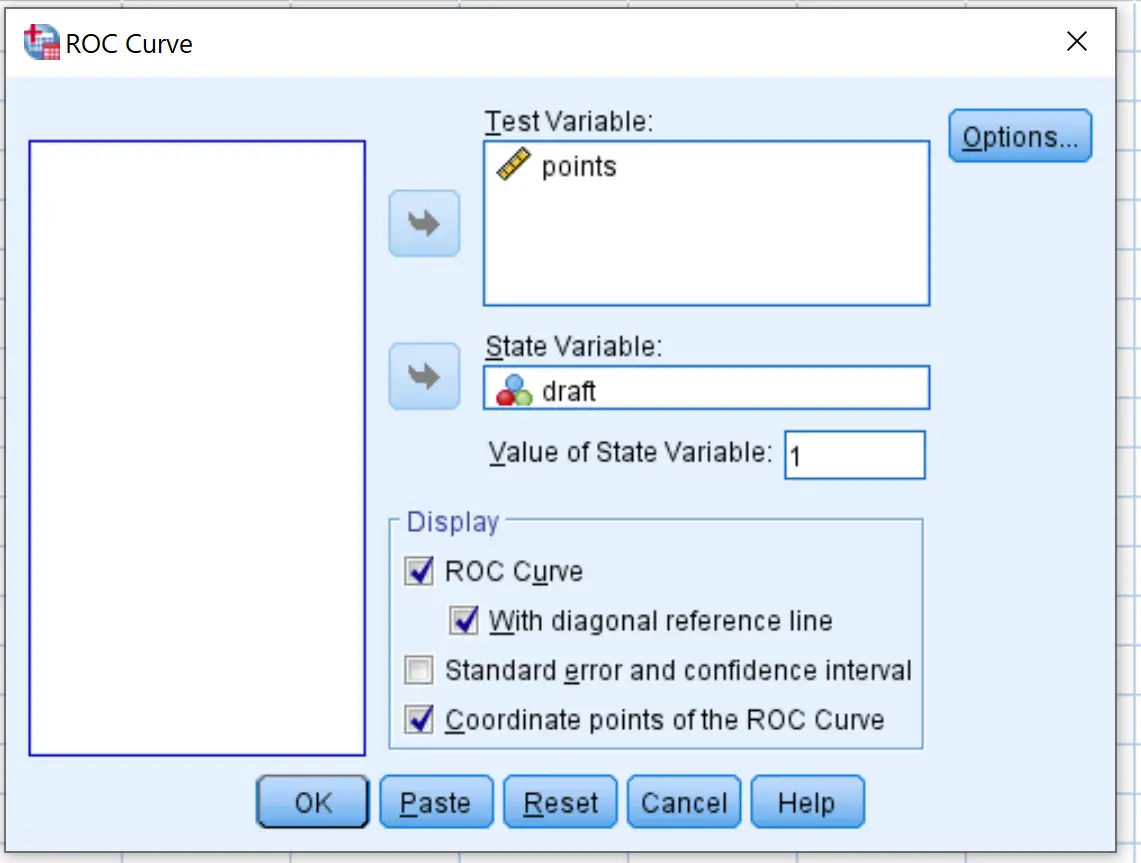
以下是如何解释结果：

文件处理总结：

此表显示数据集中正面和负面案例的总数。在此示例中，8 名球员被选中（正结果），6 名球员未被选中（负结果）：

ROC曲线：

受试者工作特征（ROC）曲线是当阈值从 0 变化到 1 时灵敏度值与特异性 1 的关系图：

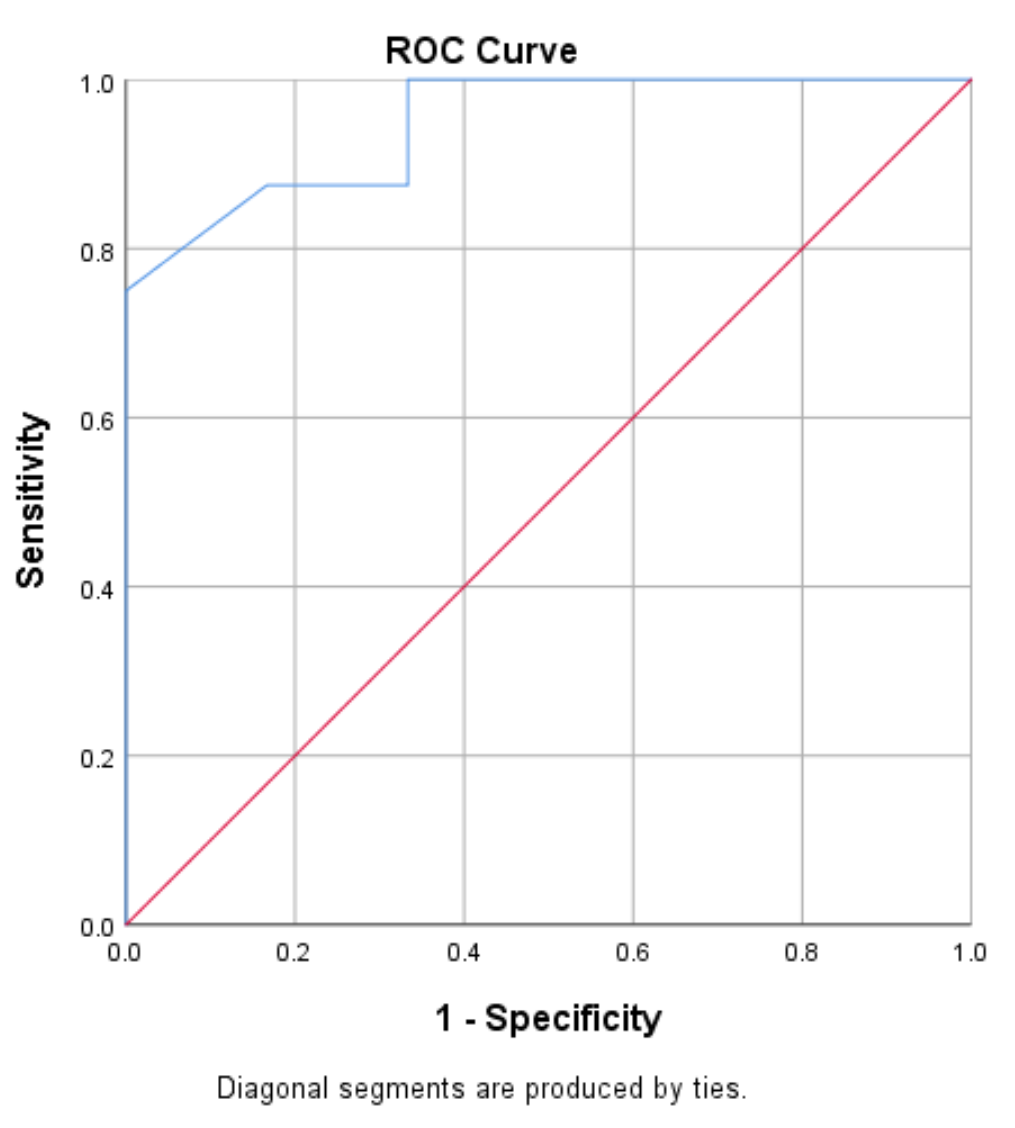
具有高灵敏度和特异性的模型将具有适合图左上角的 ROC 曲线。低灵敏度和低特异性的模型将具有接近 45 度对角线的曲线。

我们可以看到，本例中的 ROC 曲线（蓝线）紧贴图的左上角，表明该模型根据球员的场均得分很好地预测了球员是否会被选中。 。

曲线下面积：

曲线下的面积让我们了解模型区分积极结果和消极结果的能力。 AUC 的范围可以从 0 到 1。AUC 越高，模型对结果进行正确分类的能力就越好。

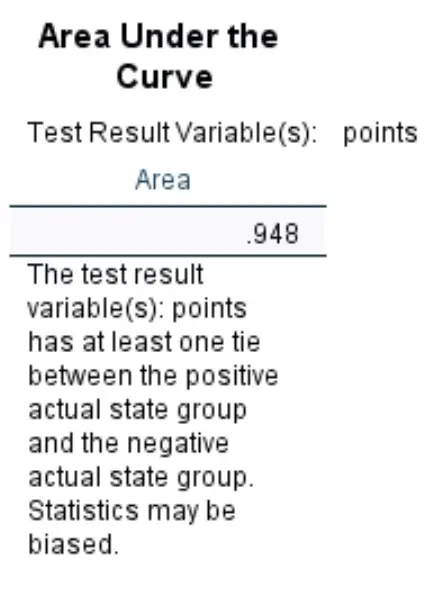
我们可以看到这个特定逻辑回归模型的 AUC 是0.948 ，这是非常高的。这表明该模型可以很好地预测球员是否会被选中。

曲线坐标：

最后一个表显示了不同阈值的 ROC 曲线的敏感性和特异性 1。

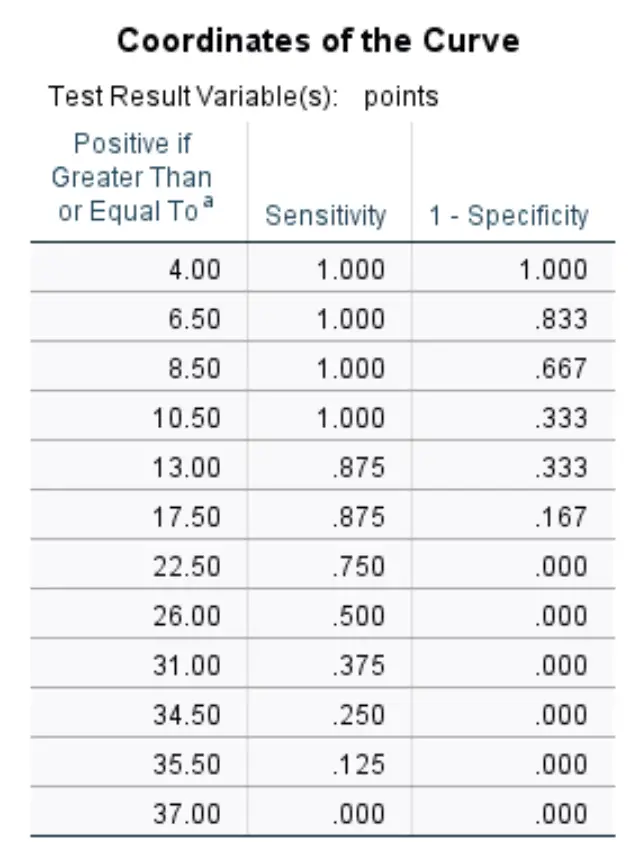
例如：

如果我们将阈值设置为8.50 ，这意味着我们预计任何场均得分低于 8.50 分的球员都不会被选中，而任何场均得分超过 8.50 分的球员都将被选中。

以此作为阈值，我们的敏感度将为 100%（因为每场比赛得分低于 8.50 分的每名球员确实都没有被选中），而我们的特异性 1将为66.7% （因为 12 名得分超过 8.50 分的球员中有 8 名）每场比赛都被选中）。

通过上表，我们可以看到每个潜在阈值的敏感性和特异性 1。