平方和简单指南:sst、ssr、sse
线性回归用于找到最“适合”一组数据的直线。
我们经常使用三个不同的平方和值来衡量回归线实际拟合数据的程度:
1. 总平方和 (SST) –各个数据点 (y i ) 与响应变量平均值 ( y ) 之差的平方和。
- 海温 = Σ(y i – y ) 2
2. 平方和回归 (SSR) – 预测数据点 (ŷ i ) 与响应变量平均值 ( y ) 之间的差值的平方和。
- SSR = Σ(ŷ i – y ) 2
3. 误差平方和 (SSE) – 预测数据点 (ŷ i ) 与观测数据点 (y i ) 之间差异的平方和。
- SSE = Σ(ŷ i – y i ) 2
这三个度量之间存在以下关系:
SST = SSR + SSE
因此,如果我们知道其中两个测量值,我们就可以使用简单的代数来计算第三个测量值。
SSR、SST 和 R 方
R 平方,有时称为决定系数,是衡量线性回归模型对数据集拟合程度的指标。它表示响应变量中可以由预测变量解释的方差的比例。
R 平方值的范围为 0 到 1。值 0 表示响应变量根本无法由预测变量解释。值为 1 表示响应变量可以由预测变量完美解释,没有错误。
使用 SSR 和 SST,我们可以计算 R 平方,如下所示:
R 平方 = SSR / SST
例如,如果给定回归模型的 SSR 为 137.5,SST 为 156,我们将按如下方式计算 R 平方:
R 平方 = 137.5 / 156 = 0.8814
这告诉我们,响应变量中 88.14% 的变异可以通过预测变量来解释。
计算 SST、SSR、SSE:分步示例
假设我们有以下数据集,显示了六名不同学生的学习小时数以及他们的期末考试成绩:
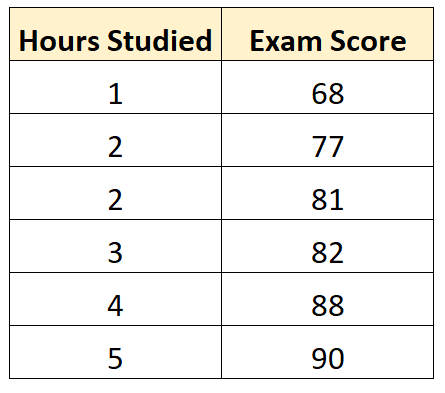
使用一些统计软件(如R 、 Excel 、Python )甚至手工,我们可以看到最佳拟合线是:
分数 = 66.615 + 5.0769*(小时)
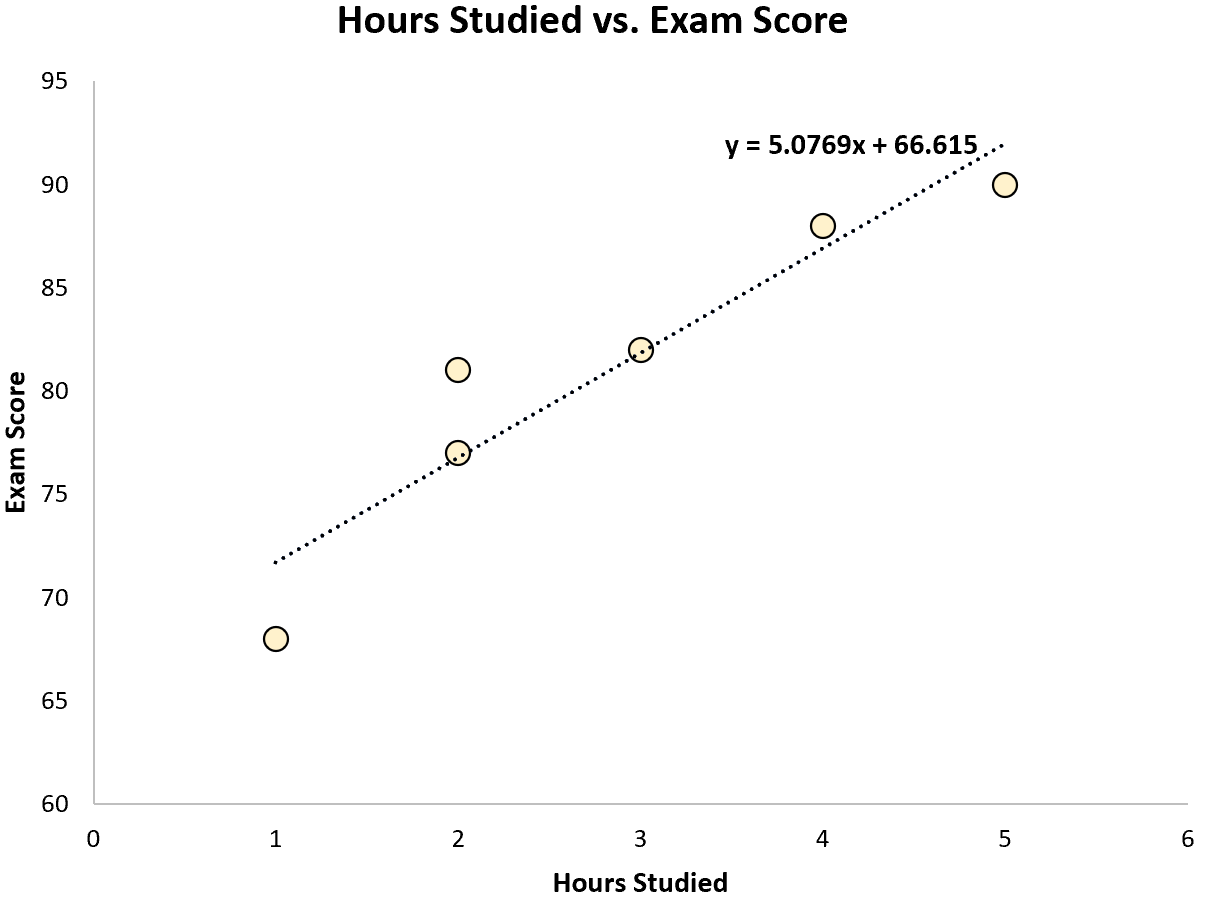
一旦我们知道了最佳拟合方程的直线,我们就可以使用以下步骤来计算 SST、SSR 和 SSE:
步骤 1:计算响应变量的平均值。
响应变量 ( y ) 的平均值为81 。
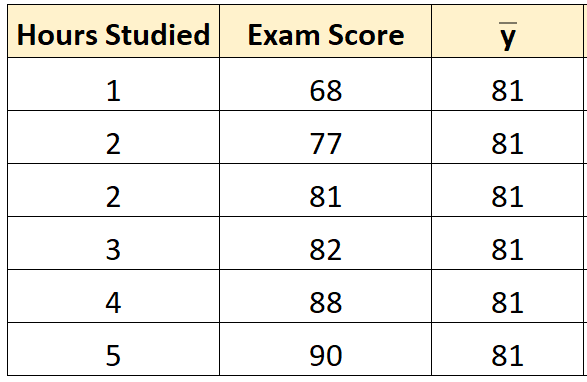
步骤 2:计算每个观测值的预测值。
然后我们可以使用最佳拟合方程的直线来计算每个学生的预测考试分数 ()。
例如,学习一小时的学生的预测考试成绩为:
分数 = 66.615 + 5.0769*(1) = 71.69 。
我们可以使用相同的方法来找到每个学生的预测分数:
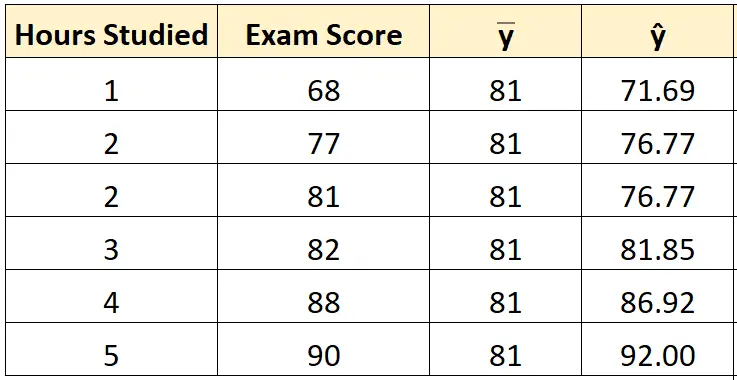
步骤 3:计算总平方和 (SST)。
然后我们就可以计算总的平方和了。
例如,第一个学生的总平方和为:
(y i – y ) 2 = (68 – 81) 2 = 169 。
我们可以使用相同的方法来计算每个学生的总平方和:
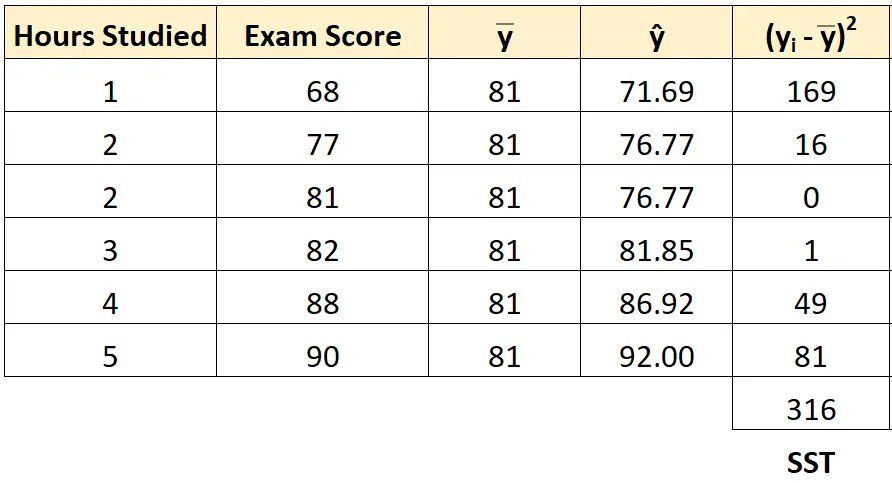
总平方和为316 。
步骤 4:计算平方和回归 (SSR)。
然后我们可以计算平方和回归。
例如,第一个学生的平方和回归为:
( ŷi – y ) 2 = (71.69 – 81) 2 = 86.64 。
我们可以使用相同的方法来找到每个学生的平方和的回归:
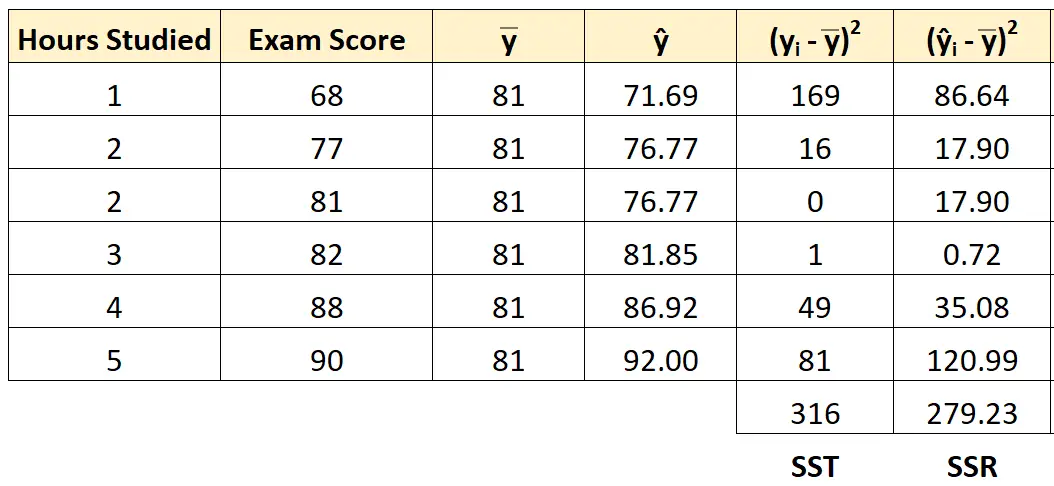
平方和回归结果为279.23 。
步骤 5:计算误差平方和 (SSE)。
然后我们就可以计算平方和的误差。
例如,第一个学生的误差平方和为:
(ŷ i – y i ) 2 = (71.69 – 68) 2 = 13.63 。
我们可以使用相同的方法来计算每个学生的误差平方和:
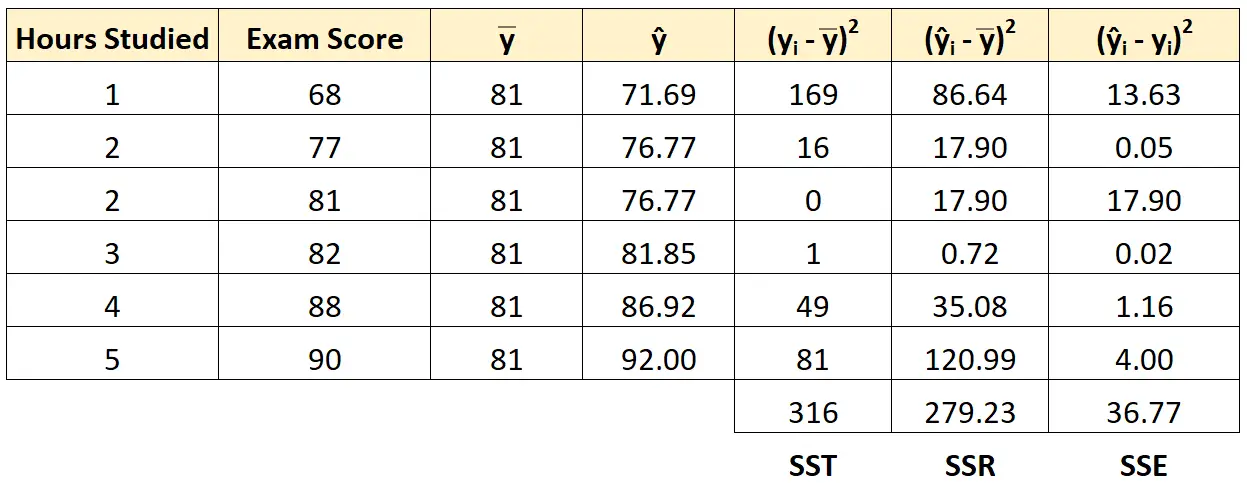
我们可以验证SST = SSR + SSE
- SST = SSR + SSE
- 316 = 279.23 + 36.77
我们还可以使用以下等式计算回归模型的 R 平方:
- R 平方 = SSR / SST
- R 平方 = 279.23 / 316
- R 平方 = 0.8836
这告诉我们, 88.36%的考试成绩差异可以通过学习时数来解释。
其他资源
您可以使用以下计算器自动计算任何简单线性回归线的 SST、SSR 和 SSE:
海温计算器
RSS 计算器
ESS计算器