统计中t值和p值的差异

学生在统计学中经常混淆的两个术语是t值和p值。

要理解这些术语之间的区别，有助于理解t 检验。

一般来说，t 检验分为三种不同类型：

• 单样本 t 检验：用于检验总体平均值是否等于某一值。
• 双样本t检验：用于检验两个总体的均值是否相等。
• 配对样本 t 检验：当一个样本中的每个观察值可以与另一个样本中的观察值相关时，用于测试两个总体的平均值是否相等。

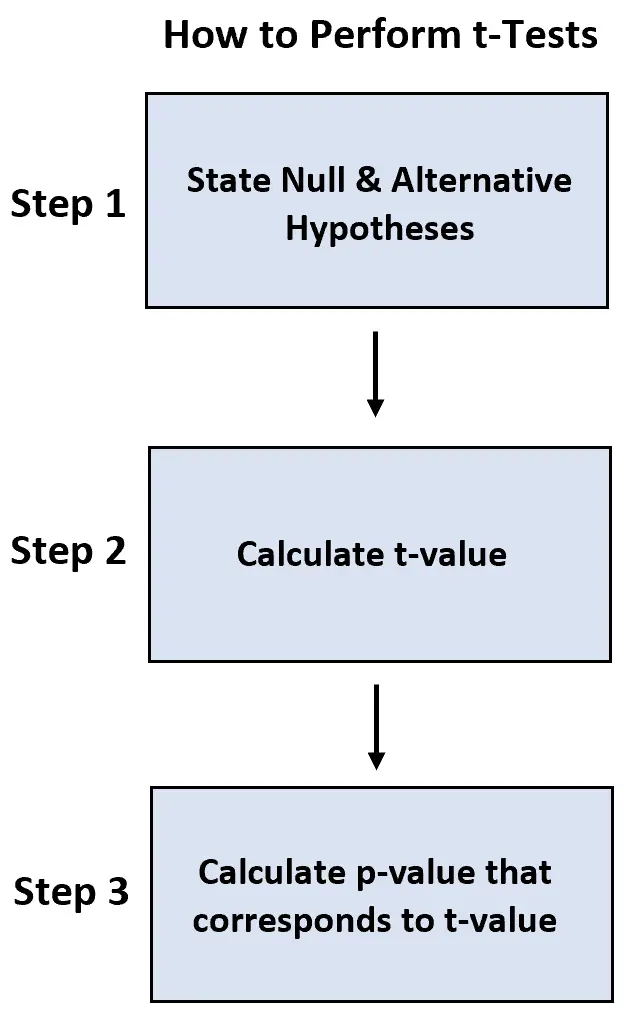
我们使用以下步骤来执行每个测试：

• 步骤 1：陈述原假设和备择假设。
• 步骤2：计算t值。
• 步骤 3：计算与 t 值对应的 p 值。

对于每个测试， t 值是量化总体均值之间差异的一种方式， p 值是获得绝对值至少与我们在“样本”中实际观察到的值一样大的 t 值的概率。数据（如果原假设确实为真）。

如果 p 值小于某个值（例如 0.05），则我们拒绝检验的原假设。

对于每种类型的 t 检验，我们对p 值感兴趣，并且我们只需使用t 值作为计算 p 值的中间步骤。

以下示例演示如何计算和解释双样本 t 检验的 t 值和相应的 p 值。

示例：计算并解释T值和P值

假设我们想知道两种不同种类的海龟的平均体重是否相等。我们从每个群体中收集 12 只海龟的简单随机样本，其权重如下：

物种 #1 ：301、298、295、297、304、305、309、298、291、299、293、304

物种#2 ：302、309、324、313、312、310、305、298、299、300、289、294

以下是如何使用此数据执行两个样本 t 检验：

步骤 1：陈述原假设和备择假设。

首先，我们将陈述原假设和备择假设：

• H ₀ : μ ₁ = μ ₂ （两个总体平均值相等）
• H ₁ : μ ₁ ≠ μ ₂ （两个总体平均值不相等）

步骤2：计算t值。

接下来，我们将每个海龟样本的权重输入二样本 t 检验计算器，发现 t 值为-1.608761 。

步骤 3：计算 p 值。

我们还可以使用双样本 t 检验计算器来查找与 t 值 -1.608761 对应的 p 值为0.121926 。

由于该 p 值不小于 0.05，因此我们无法拒绝原假设。

这意味着我们没有足够的证据表明两个种群之间海龟的平均体重不同。

请注意，我们只是使用 t 值作为计算 p 值的中间步骤。 p 值是我们感兴趣的真实值，但我们必须首先计算 t 值。

其他资源

以下教程提供有关 t 检验和 p 值的其他信息：

单样本 t 检验简介
二样本t检验简介
配对样本 t 检验简介
如何通过 t 检验手动计算 P 值