如何在 excel 中从 t 分数查找 p 值

在统计学中， 假设检验通常会产生 T 分数检验统计量。一旦我们找到了 t 分数，我们通常会找到与之相关的 p 值。如果该 p 值低于某个 alpha 水平（例如 0.10、0.05、0.01），则我们拒绝检验的原假设并得出结论：我们的结果是显着的。

本教程介绍如何使用T.DIST函数从 Excel 中的 t 分数查找 p 值，该函数采用以下参数：

T.DIST (x, deg_freedom)

金子：

• x：我们感兴趣的 T 分数。
• deg_freedom：自由度。

让我们看一些例子。

示例 1：来自 t 分数的 P 值（双尾）

植物学家想知道某种植物的平均高度是否等于 15 英寸。在 12 株植物的随机样本中，她发现样本的平均高度为 14.33 英寸，样本的标准差为 1.37 英寸。

使用 0.05 的 alpha 水平执行双尾假设检验，以确定平均高度是否等于 15 英寸。

第 1 步：陈述假设。

原假设 (H ₀ )：μ = 15

备择假设：(Ha)：μ ≠ 15

第 2 步：找到 T 分数和自由度。

得分 t = ( x -μ) / (s/√n) = (14.33-15) / (1.37/√12) = -1.694 。

自由度 = n-1 = 12-1 = 11 。

步骤 3：使用 Excel 查找 t 分数的 p 值。

为了找到 t 分数的 p 值，我们将在 Excel 中使用以下公式：

=T.DIST.2T(ABS(-1.694), 11)

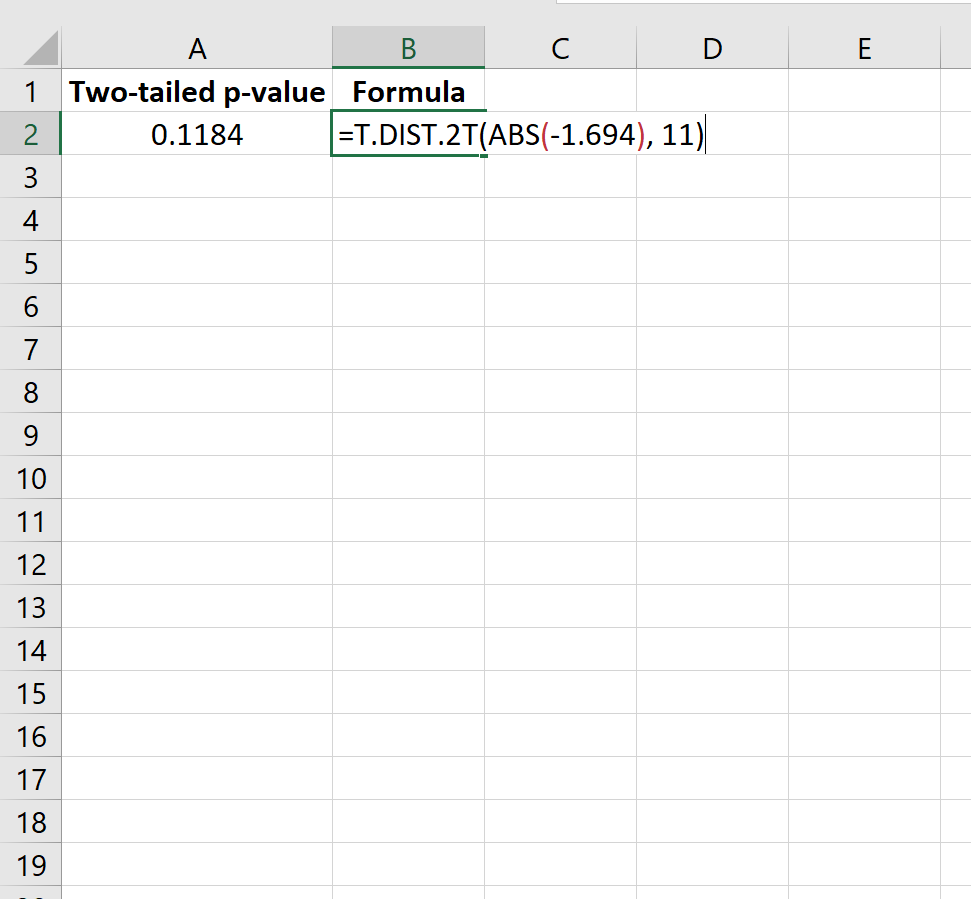
这告诉我们两侧的 p 值为0.1184 。

步骤 4：拒绝或不拒绝原假设。

由于 p 值0.1184不小于所选的 alpha 水平0.05 ，因此我们无法拒绝原假设。我们没有足够的证据表明平均植物高度不同于 15 英寸。

示例 2：T 分数的 P 值（单边）

一家公司想知道新型电池的平均寿命是否比当前标准电池（平均寿命为 18 小时）更长。他们随机抽取了 25 块新电池，发现平均寿命为 19 小时，标准差为 4 小时。

使用 0.05 的 alpha 水平进行单边假设检验，以确定新电池的平均寿命是否比当前标准电池的平均寿命长。

第 1 步：陈述假设。

原假设 (H ₀ )：μ ≤ 18

备择假设：(Ha)：μ > 18

第 2 步：找到 T 分数和自由度。

得分 t = ( x -μ) / (s/√n) = (19-18) / (4/√25) = 1.25 。

自由度 = n-1 = 25-1 = 24 。

步骤 3：使用 Excel 查找 t 分数的 p 值。

为了找到 t 分数的 p 值，我们将在 Excel 中使用以下公式：

=T.DIST.RT(1.25, 24)

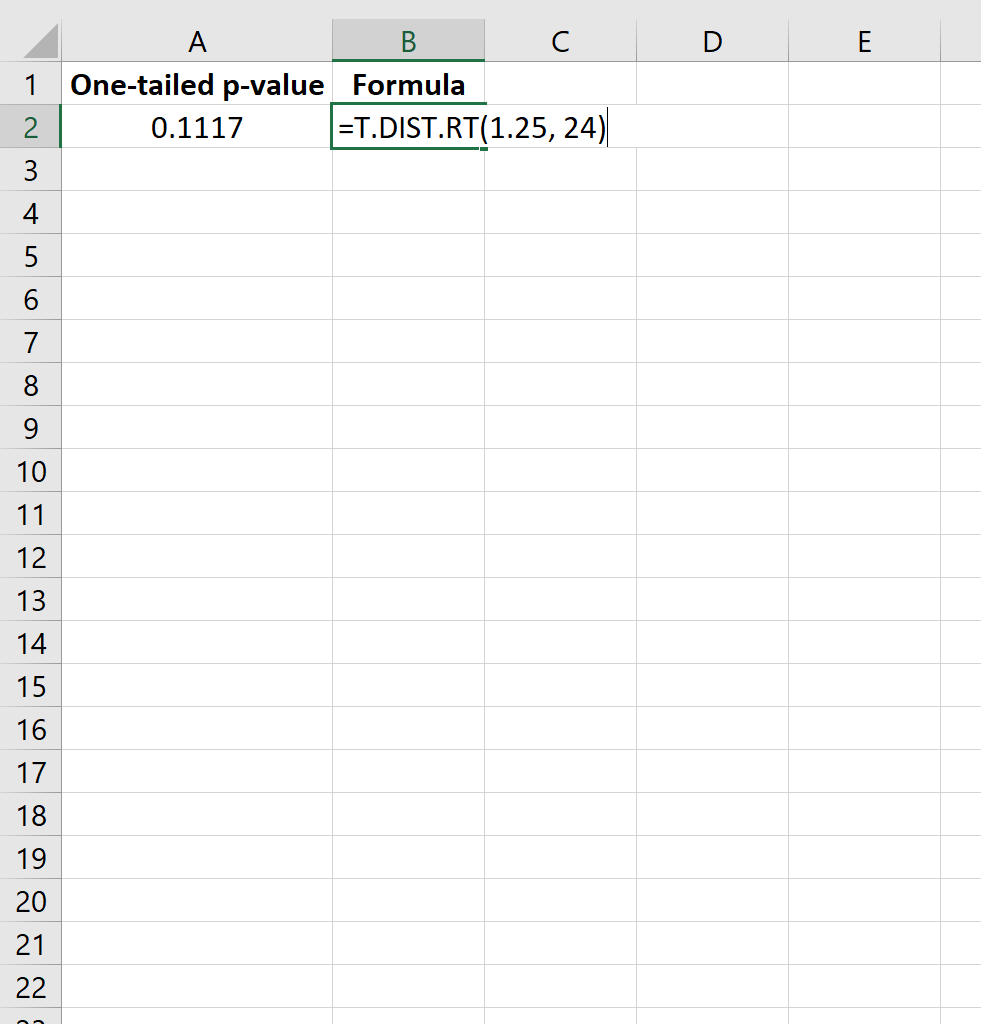
这告诉我们单边 p 值为0.1117 。

步骤 4：拒绝或不拒绝原假设。

由于 p 值0.1117大于所选的 alpha 水平0.05 ，因此我们无法拒绝原假设。我们没有足够的证据表明新电池的平均寿命比当前标准电池的平均寿命更长。

有关 Excel 统计的更多教程，请务必查看我们完整的Excel 指南列表。