如何使用不相等的样本量执行 t 检验

当谈到统计时，学生经常问的一个问题是：

各组样本量不等时是否可以进行t检验？

简短的回答：

是的，当样本量不相等时，您可以执行 t 检验。相同的样本量不是 t 检验中所做的假设之一。

当两个样本的方差不相等时，真正的问题就会出现，这是t 检验中所做的假设之一。

发生这种情况时，建议改用韦尔奇 t 检验，该检验不假设方差相等。

以下示例展示了当方差相等和不相等时如何使用不相等的样本量执行 T 检验。

示例 1：样本量不相等且方差相等

假设我们管理两个旨在帮助学生在某些考试中取得更好成绩的计划。

结果如下：

方案一：

• n （样本量）：500
• x （样本平均值）：80
• s （样本标准差）：5

方案2：

• n （样本量）：20
• x （样本平均值）：85
• s （样本标准差）：5

以下代码展示了如何在 R 中创建箱线图以可视化每个程序的考试分数分布：

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=5)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

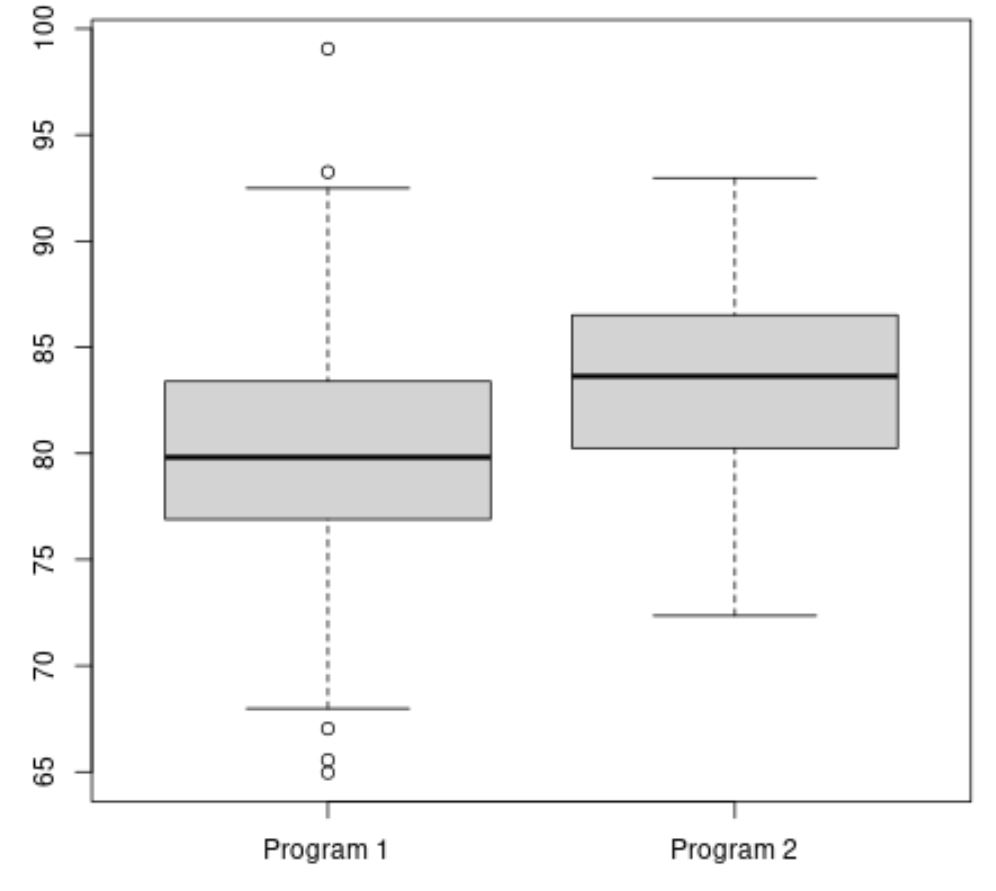
项目 2 的平均考试成绩似乎更高，但两个项目之间的考试成绩差异大致相等。

以下代码显示如何使用 Welch t 检验执行独立样本 t 检验：

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -3.3348, df = 518, p-value = 0.0009148
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.111504 -1.580245
sample estimates:
mean of x mean of y 
 80.11322 83.95910

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -3.3735, df = 20.589, p-value = 0.00293
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.219551 -1.472199
sample estimates:
mean of x mean of y 
 80.11322 83.95910 

独立样本 t 检验返回 p 值为0.0009 ，而 Welch t 检验返回 p 值为0.0029 。

由于每个测试的 p 值小于 0.05，因此我们会拒绝每个测试中的原假设，并得出结论：两个项目之间的平均考试成绩存在统计上的显着差异。

尽管样本量不相等，但独立样本 t 检验和 Welch t 检验都返回相似的结果，因为两个样本具有相等的方差。

示例 2：不等的样本量和不等的方差

假设我们管理两个旨在帮助学生在某些考试中取得更好成绩的计划。

结果如下：

方案一：

• n （样本量）：500
• x （样本平均值）：80
• s （样本标准差）：25

方案2：

• n （样本量）：20
• x （样本平均值）：85
• s （样本标准差）：5

以下代码展示了如何在 R 中创建箱线图以可视化每个程序的考试分数分布：

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=25)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

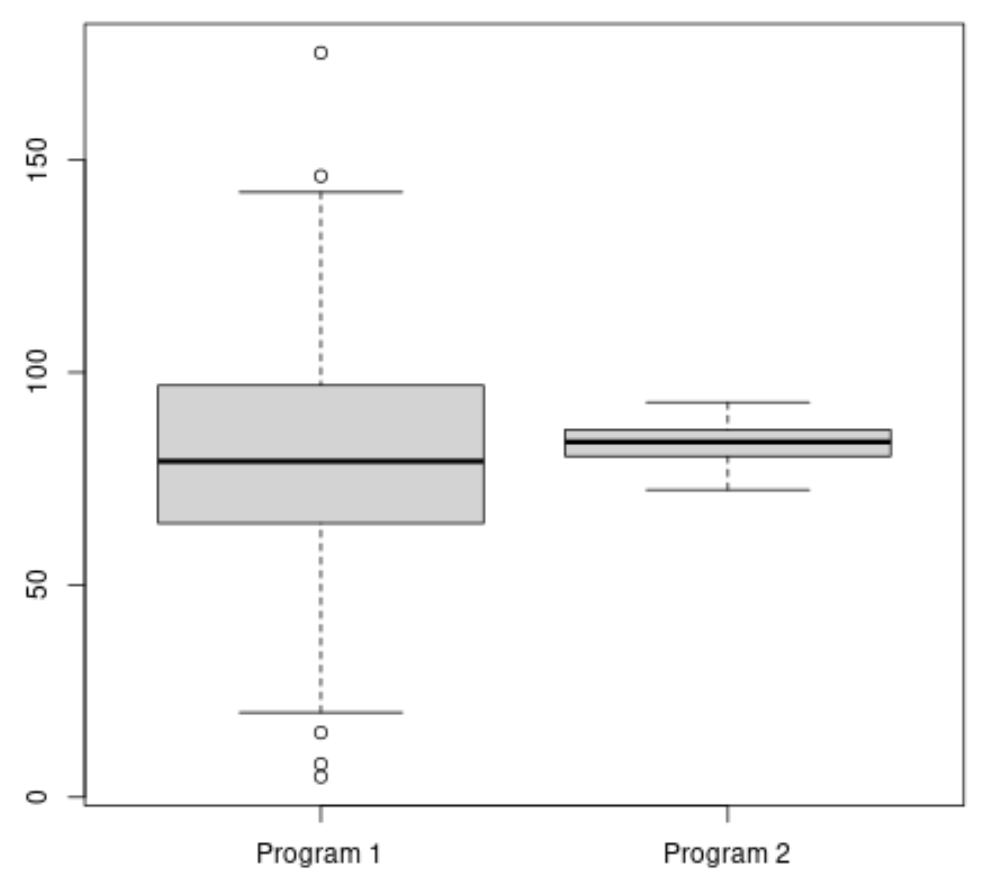
项目 2 的平均考试成绩似乎更高，但项目 1 的考试成绩方差远高于项目 2。

以下代码显示如何使用 Welch t 检验执行独立样本 t 检验：

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -0.5988, df = 518, p-value = 0.5496
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -14.52474 7.73875
sample estimates:
mean of x mean of y 
  80.5661 83.9591

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -2.1338, df = 74.934, p-value = 0.03613
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.560690 -0.225296
sample estimates:
mean of x mean of y 
  80.5661 83.9591 

独立样本 t 检验返回的 p 值为0.5496 ，而 Welch t 检验返回的 p 值为0.0361 。

独立样本 t 检验无法检测平均考试成绩的差异，但韦尔奇 t 检验能够检测统计显着性差异。

由于两个样本的方差不相等，因此只有韦尔奇 t 检验能够检测平均考试成绩的统计显着性差异，因为该检验不假设样本之间的方差相等。

其他资源

以下教程提供有关 t 检验的其他信息：

单样本 t 检验简介
双样本 t 检验简介
配对样本 t 检验简介