了解线性回归中的 t 检验
线性回归用于量化预测变量和响应变量之间的关系。
每当我们进行线性回归时,我们都想知道预测变量和响应变量之间是否存在统计上显着的关系。
我们通过对回归斜率执行 t 检验来检验显着性。我们对此 t 检验使用以下原假设和备择假设:
- H 0 : β 1 = 0(斜率为零)
- H A : β 1 ≠ 0 (斜率不为零)
然后我们计算检验统计量如下:
t = b / SE b
金子:
- b :系数的估计
- SE b :系数估计的标准误差
如果对应于t 的p 值低于某个阈值(例如 α = 0.05),则我们拒绝原假设并得出结论:预测变量和响应变量之间存在统计上显着的关系。
以下示例展示了如何在实践中对线性回归模型执行 t 检验。
示例:运行线性回归的 t 检验
假设一位教授想要分析 40 名学生的学习时间和考试成绩之间的关系。
它使用学习时间作为预测变量和收到的考试成绩作为响应变量来执行简单的线性回归。
下表显示了回归模型的结果:
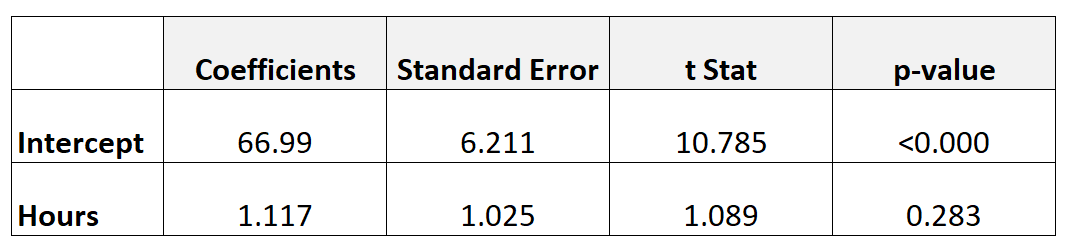
为了确定学习时间与期末考试成绩是否具有统计显着关系,我们可以进行 t 检验。
我们对此 t 检验使用以下原假设和备择假设:
- H 0 : β 1 = 0(研究时间的斜率等于零)
- H A : β 1 ≠ 0(研究时间的斜率不等于零)
然后我们计算检验统计量如下:
- t = b / SE b
- t = 1.117 / 1.025
- t = 1.089
对应于t = 1.089 且 df = n-2 = 40 – 2 = 38 的 p 值为0.283 。
请注意,我们还可以使用T 分数到 P 值计算器来计算此 p 值:

由于该 p 值不小于 0.05,因此我们无法拒绝原假设。
这意味着学习时间与期末考试成绩之间没有统计学上的显着关系。
其他资源
以下教程提供有关线性回归的其他信息: