如何在 ti-84 计算器上执行二次回归
当两个变量存在线性关系时,我们通常可以使用简单线性回归来量化它们的关系。

然而,当两个变量存在二次关系时,我们可以使用二次回归来量化它们的关系。

本教程介绍如何在 TI-84 计算器上执行二次回归。
示例:TI-84 计算器上的二次回归
假设我们想了解工作时间与幸福感之间的关系。我们有以下关于 11 名不同的人每周工作时数和报告的幸福程度(范围为 0 到 100)的数据:

按照以下步骤在 TI-84 计算器上执行二次回归。
步骤 1:可视化数据。
在使用二次回归之前,我们必须确保解释变量(小时)和响应变量(幸福)之间的关系确实是二次关系。
首先,我们将输入解释变量和响应变量的数据值。按统计,然后按编辑。在 L1 列中输入解释变量(工作时间)的以下值,并在 L2 列中输入响应变量(幸福)的值:
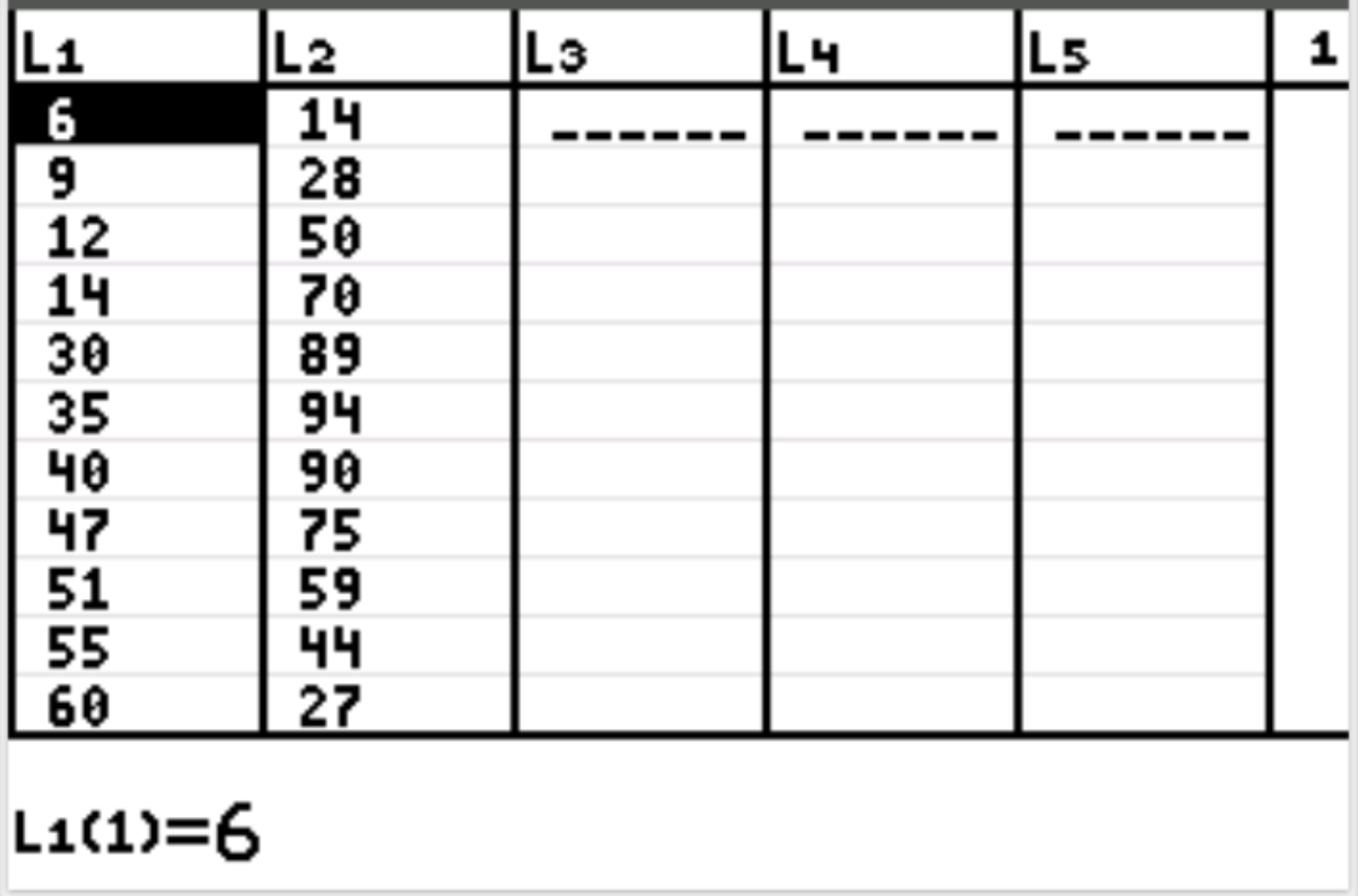
接下来,按2nd ,然后按y=访问statplot菜单。突出显示 Plot1 并按Enter 。确保启用绘图并分别为 Xlist 和 Ylist 选择 L1 和 L2:
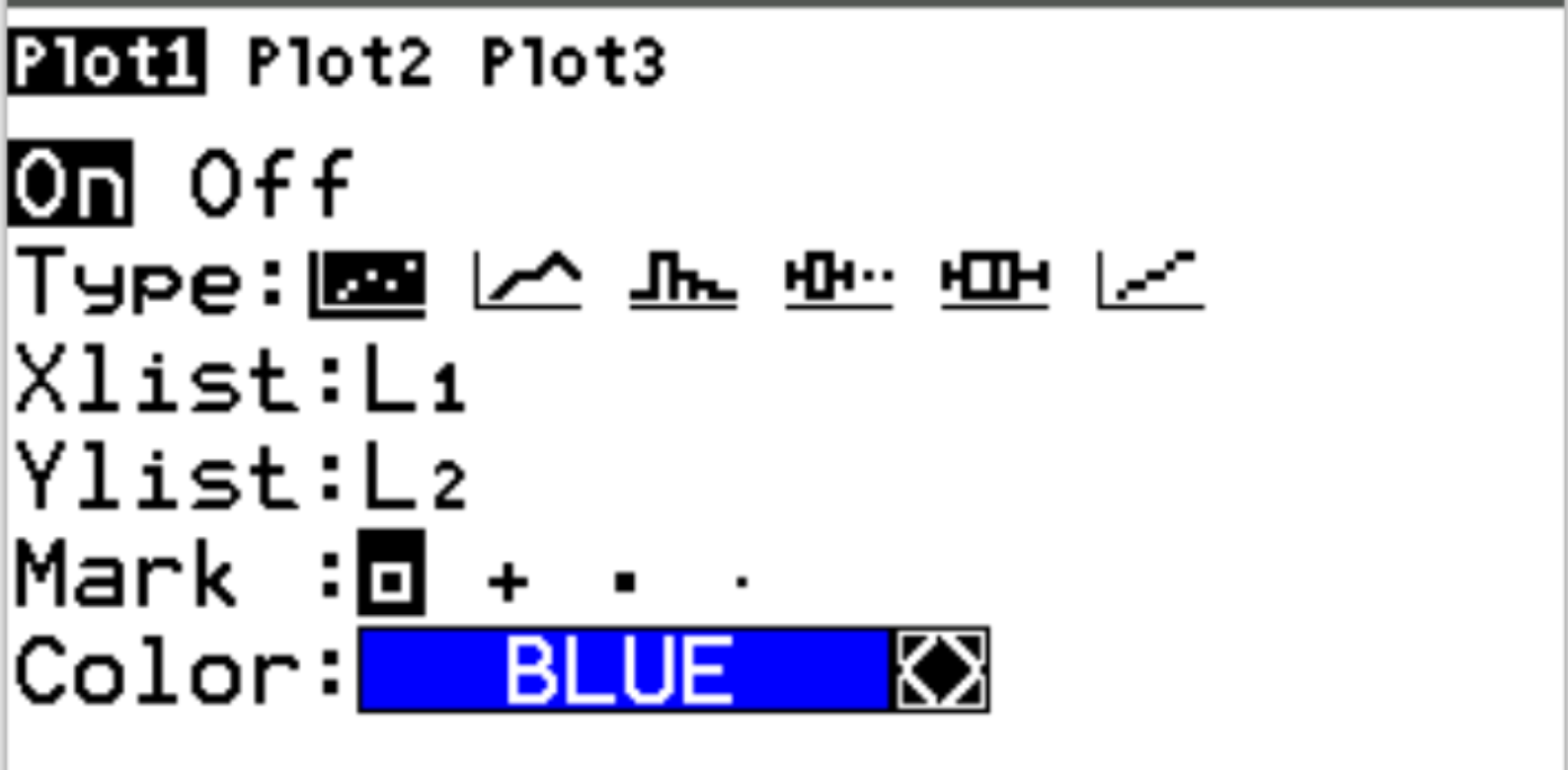
接下来,按Zoom ,然后按9:ZoomStat 。这将自动生成以下点云:

我们可以看到,随着工作时间从零增加到某个点,幸福感往往会增加,但随着工作时间进一步增加,幸福感开始下降。
散点图中的倒“U”形表明工作时间和幸福感之间存在二次关系,这意味着我们应该使用二次回归来量化这种关系。
步骤 2:执行二次回归。
接下来,我们将执行二次回归。按Stat ,然后滚动至CALC 。然后滚动到5:QuadReg并按Enter 。
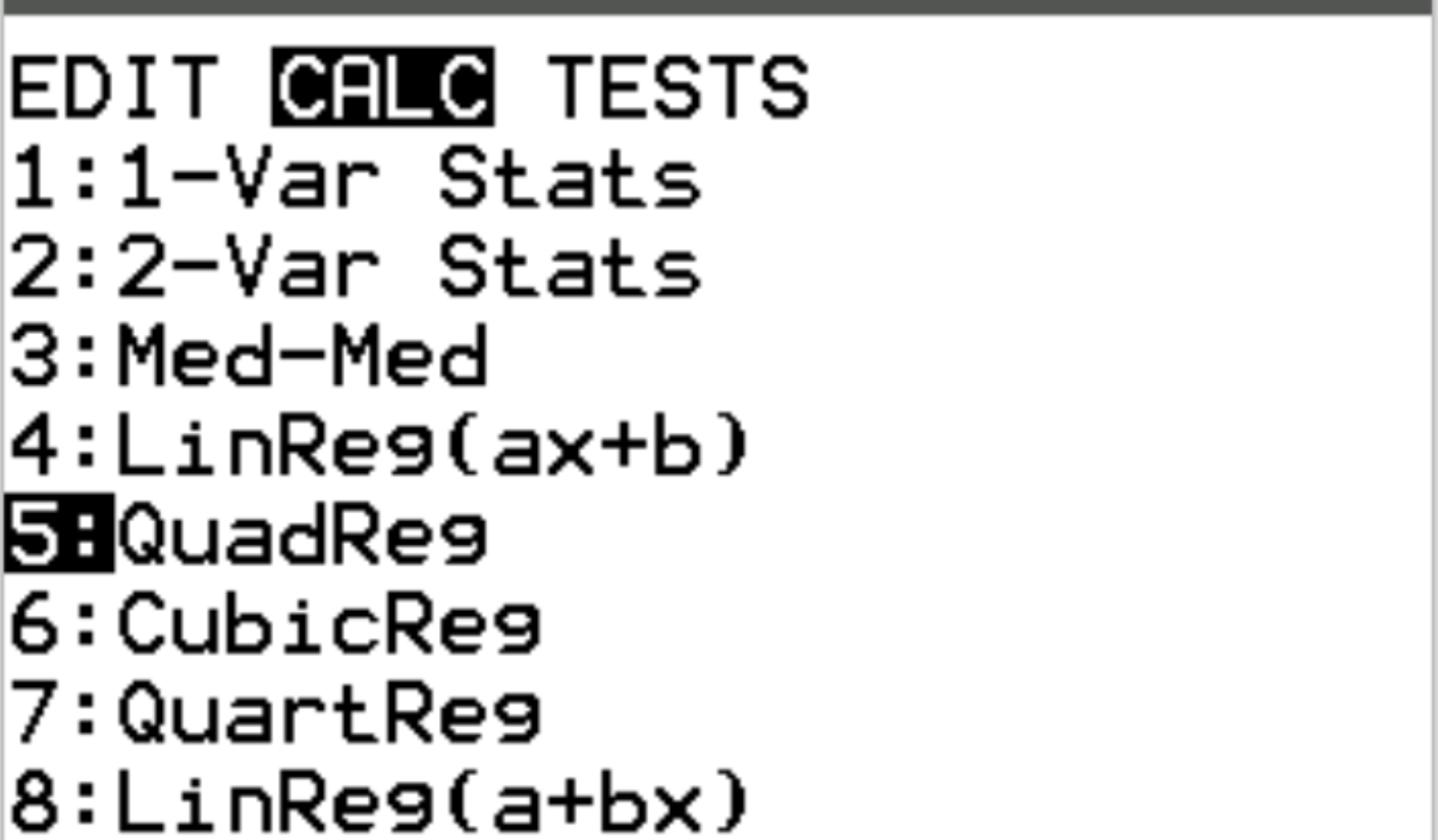
对于 Xlist 和 Ylist,请确保选择 L1 和 L2,因为这些是我们用来输入数据的列。将FreqList留空。向下滚动到计算并按Enter 。
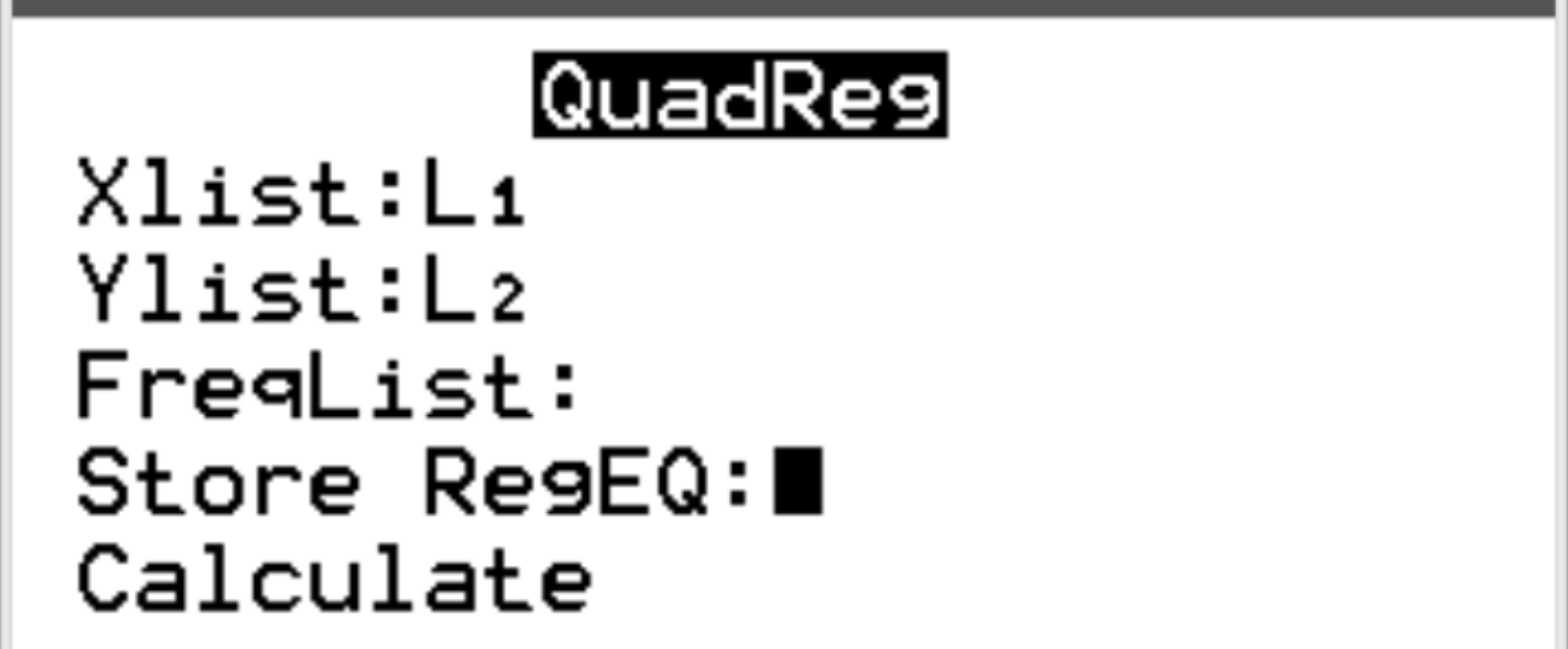
将自动出现以下输出:
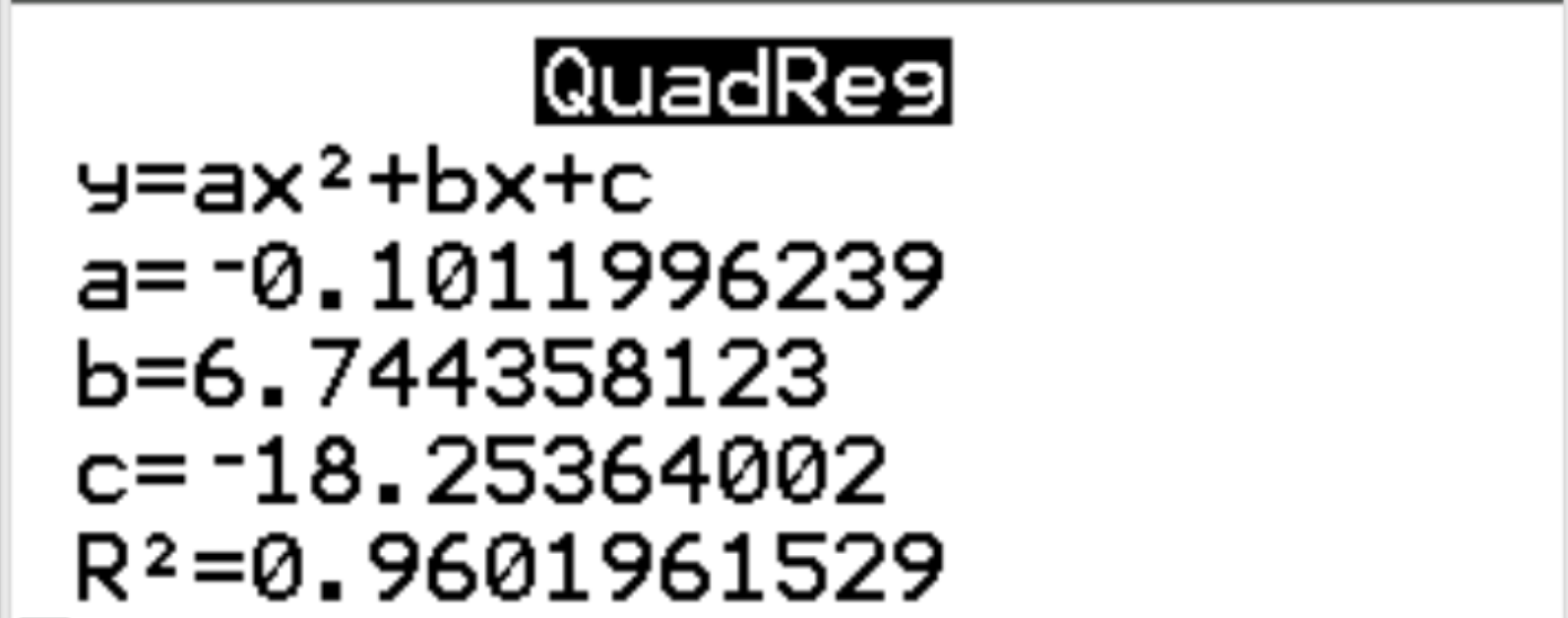
步骤 3:解释结果。
从结果中我们可以看出,估计的回归方程为:
幸福 = -0.1012(小时) 2 + 6.7444(小时)– 18.2536
我们可以使用这个方程来计算一个人在每周工作时数的情况下的预期幸福感。
例如,一个每周工作 60 小时的人的幸福指数为22.09 :
幸福 = -0.1012(60) 2 + 6.7444(60) – 18.2536 = 22.09
相反,每周工作 30 小时的人的幸福指数应该为92.99 :
幸福感 = -0.1012(30) 2 + 6.7444(30) – 18.2536 = 92.99
我们还可以看到回归模型的 r 平方为 r 2 = 0.9602 。这是可以由解释变量解释的响应变量方差的比例。在这个例子中,96.02% 的幸福感变化可以用小时和时间来解释2 。