如何在 excel 中执行 tukey-kramer 事后检验
单向方差分析用于确定三个或更多独立组的平均值之间是否存在统计显着差异。
方差分析中使用的假设如下:
原假设 (H 0 ): µ 1 = µ 2 = µ 3 = … = µ k (每组的平均值相等)
备择假设:(Ha):至少其中一个均值与其他均值不同
如果方差分析的p 值低于显着性水平,我们可以拒绝原假设,并得出结论:我们有足够的证据表明组均值中至少有一个与其他均值不同。
然而,这并没有告诉我们哪些群体彼此不同。这只是告诉我们并非所有组的平均值都是相等的。为了准确地了解哪些组彼此不同,我们需要执行事后测试。
最常用的事后检验是Tukey-Kramer 检验,它比较每个成对组组合之间的平均值。
以下示例显示如何在 Excel 中执行 Tukey-Kramer 检验。
示例:Excel 中的 Tukey-Kramer 检验
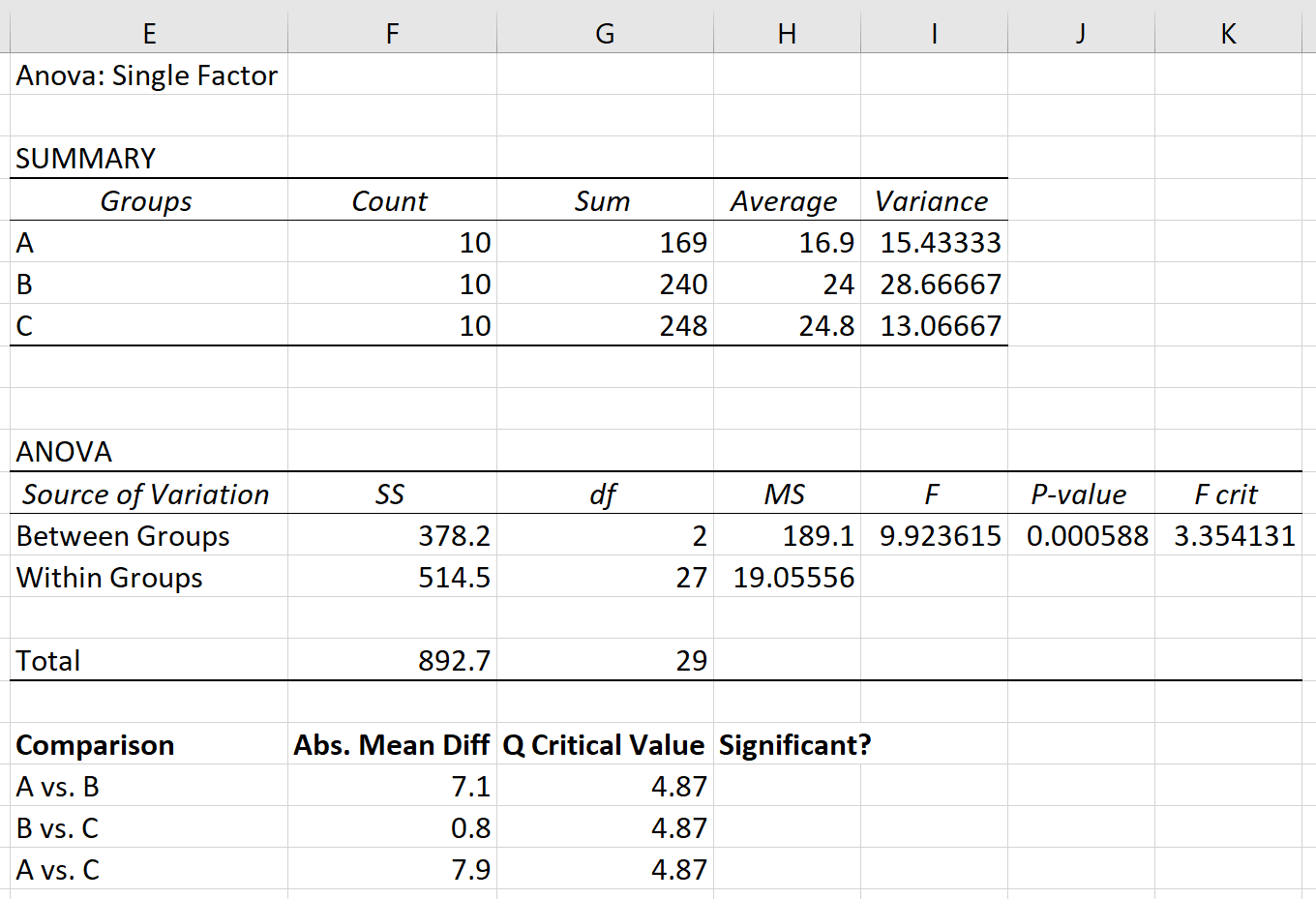
假设我们对 A、B 和 C 三组进行单向方差分析。单向方差分析的结果如下所示:
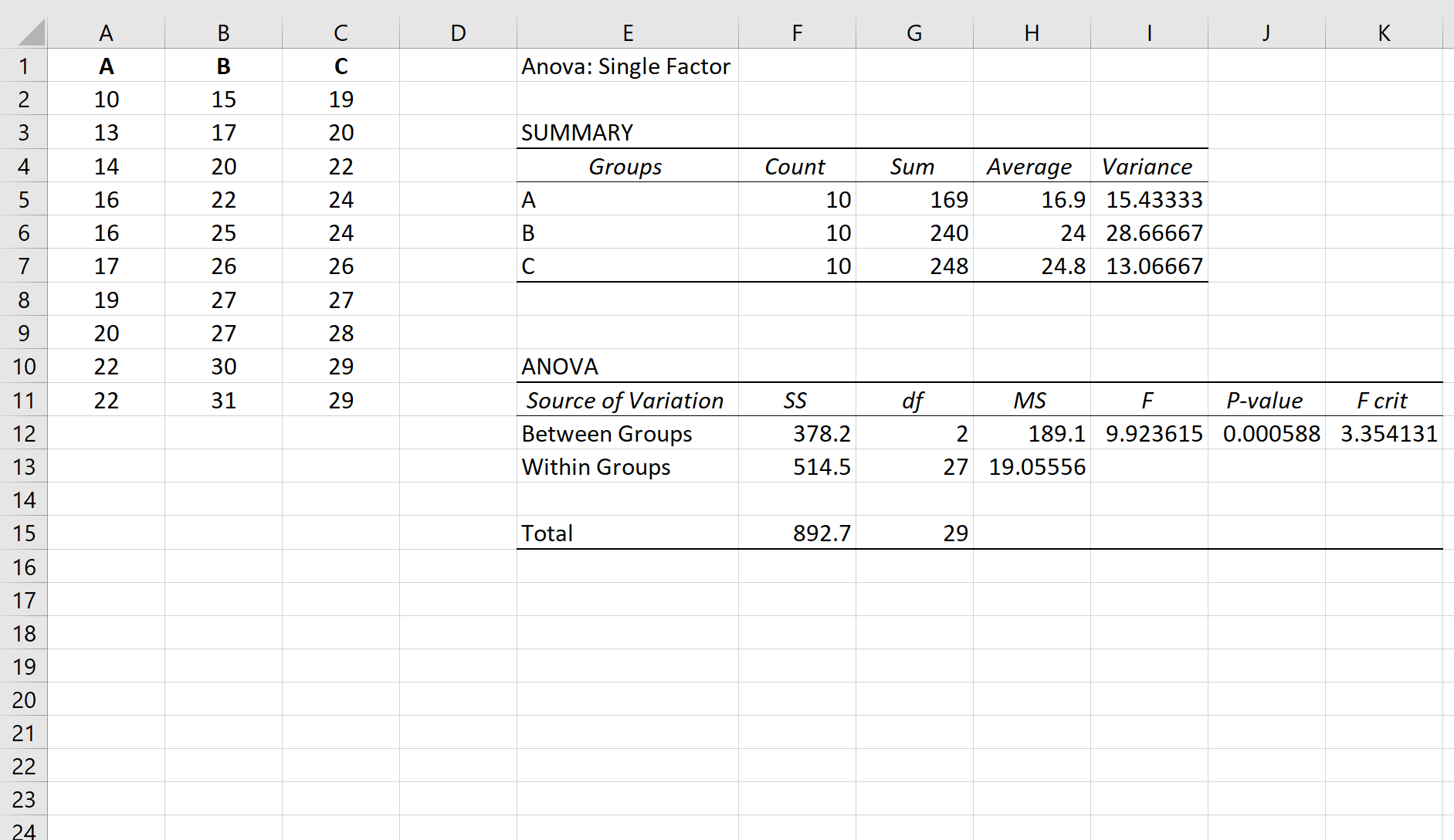
方差分析表的 p 值为0.000588 。由于该 p 值小于 0.05,因此我们可以拒绝原假设并得出结论:三组之间的均值不相等。
为了准确确定哪个组均值不同,我们可以使用以下步骤执行 Tukey-Kramer 事后检验:
步骤 1:找出每组之间的绝对平均差。
首先,我们将使用方差分析结果第一个表中列出的平均值找到每组之间的绝对平均差:
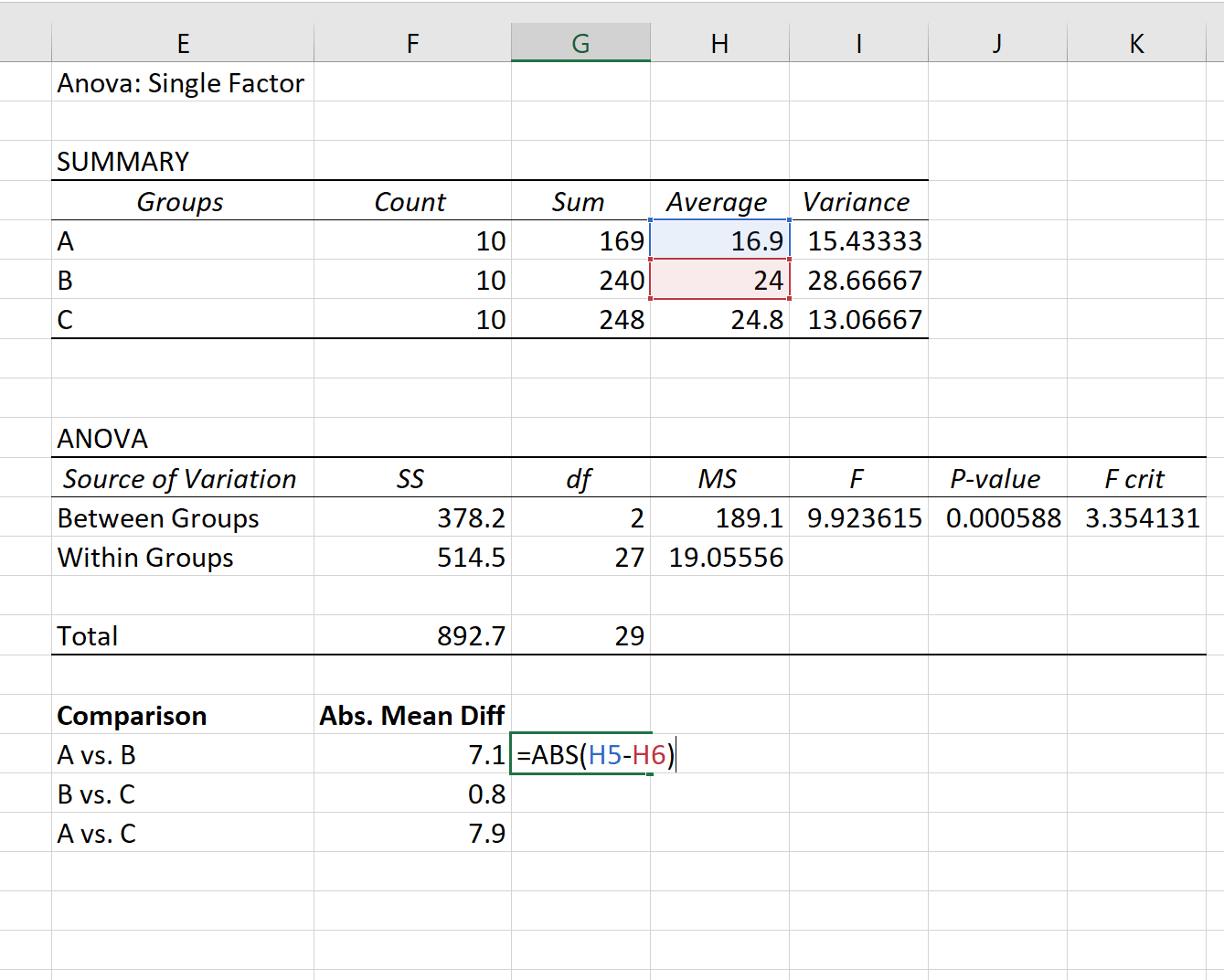
步骤2:求Q的临界值。
接下来,我们需要使用以下公式找到 Q 的临界值:
临界值 Q = Q*√(s 2分组/ n.)
金子:
- Q = Student 表 Q 范围的值
- s 2 pooled =所有组的方差汇总
- 不是。 = 给定组的样本量
要找到 Q 值,您可以参考学生化范围 Q 表,如下所示:
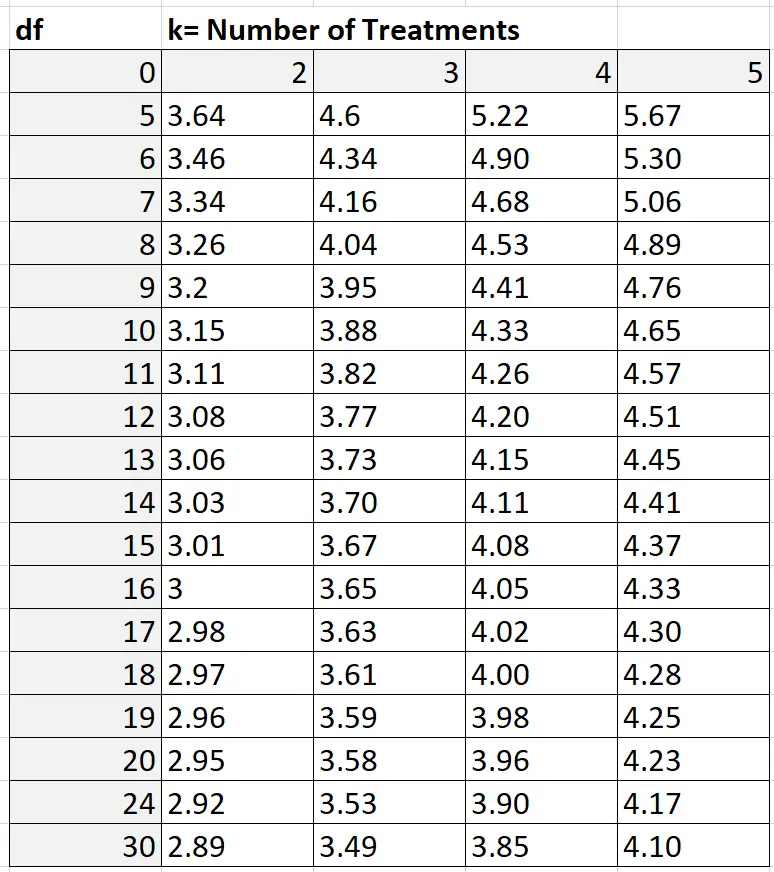
在我们的示例中,k = 组数,即 k = 3。自由度计算如下:nk = 30 – 3 = 27。由于上表中未显示 27,因此我们可以使用保守估计 24 . 根据 k = 3 和 df = 24,我们发现 Q = 3.53 。
合并方差可以计算为各组方差的平均值,结果为19.056 。
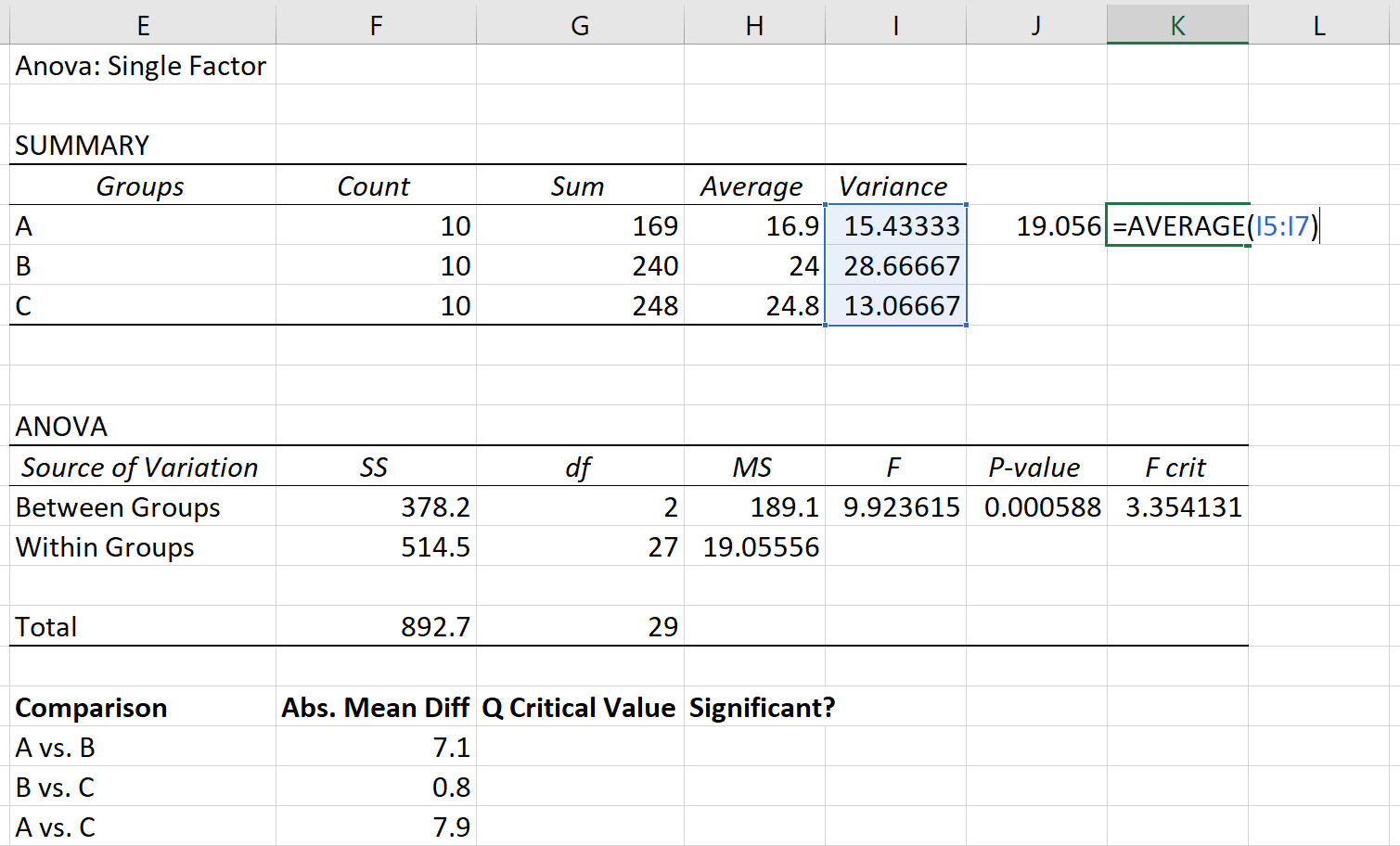
最后,每组的样本量为10。
因此,我们的临界值Q可以计算如下:
临界值Q = Q*√(s 2分组/n.) = 3.53*√(19.056/10) = 4.87 。
步骤 3:确定哪组均值不同。
最后,我们可以将每组之间的绝对均值差与临界值 Q 进行比较。如果绝对均值差大于临界值 Q,则组均值之间的差异具有统计显着性:
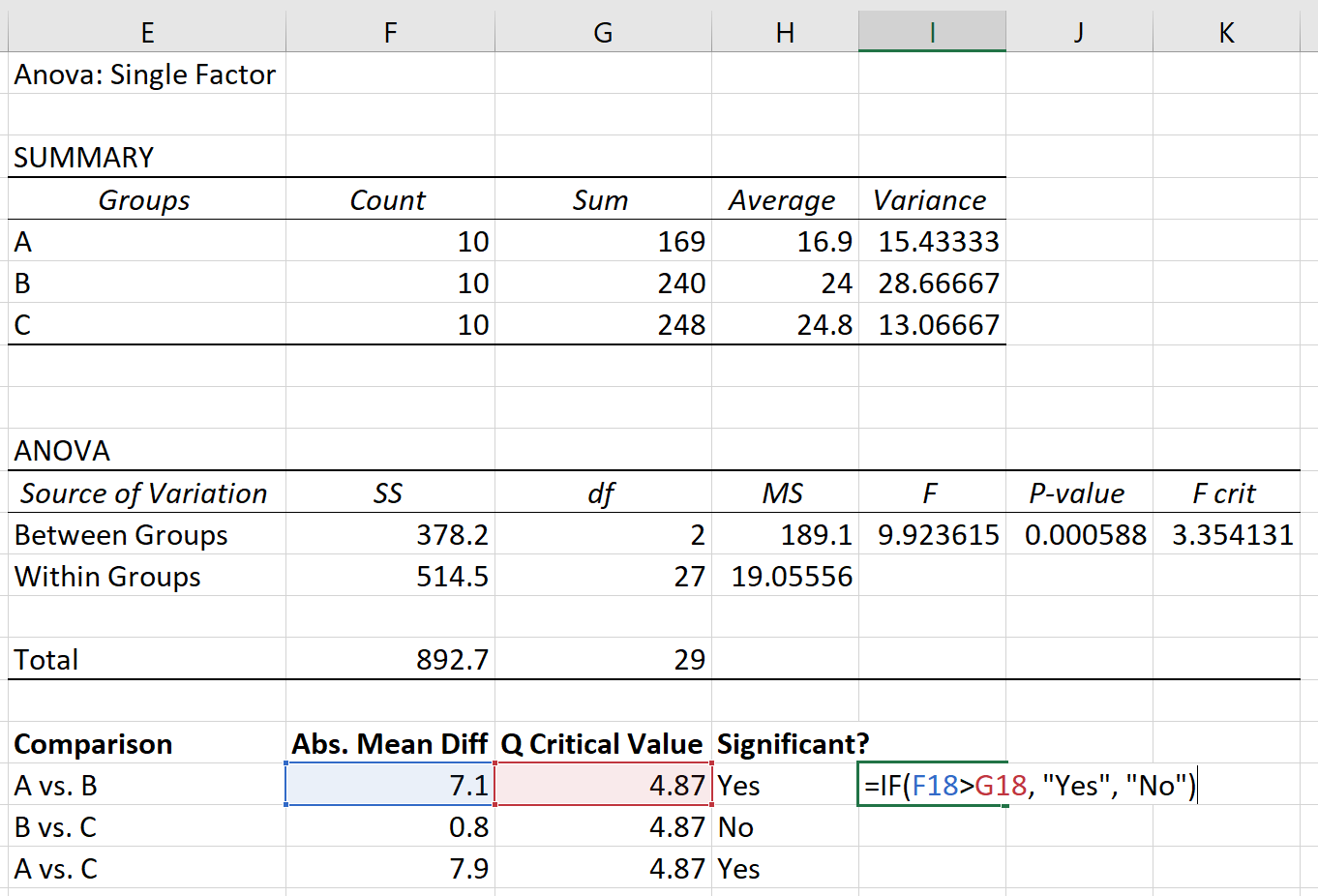
根据 Tukey-Kramer 事后测试,我们发现以下内容:
- A 组和 B 组之间的平均值差异具有统计学意义。
- B组和C组之间的平均值差异不具有统计学意义。
- A 组和 C 组之间的平均值差异具有统计学意义。