如何执行相关 t 检验
皮尔逊相关系数用于量化两个变量之间的线性关联。
它始终采用 -1 和 1 之间的值,其中:
- -1 表示完全负线性相关。
- 0 表示没有线性相关。
- 1 表示完全正线性相关。
要确定相关系数是否具有统计显着性,您可以执行 t 检验,其中涉及计算 t 分数和相应的 p 值。
t-score的计算公式如下:
t = r√ (n-2) / (1-r 2 )
金子:
- r:相关系数
- n:样本量
p 值计算为具有 n-2 自由度的 t 分布的相应双尾 p 值。
以下示例显示如何对相关系数执行 t 检验。
示例:运行相关性 t 检验
假设我们有以下包含两个变量的数据集:
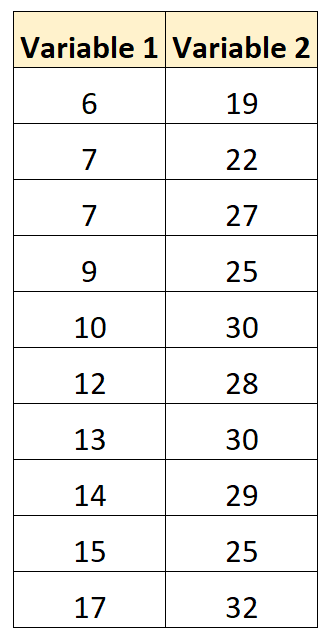
使用一些统计软件(Excel、R、Python等),我们可以计算出两个变量之间的相关系数为0.707 。
这是一个非常正相关的关系,但要确定它是否具有统计显着性,我们需要计算相应的 t 分数和 p 值。
我们可以如下计算 t 分数:
- t = r√ (n-2) / (1-r 2 )
- t = 0.707√ (10-2) / (1-0.707 2 )
- t = 2.828
使用P 值 T 分数计算器,我们发现相应的 p 值为0.022 。
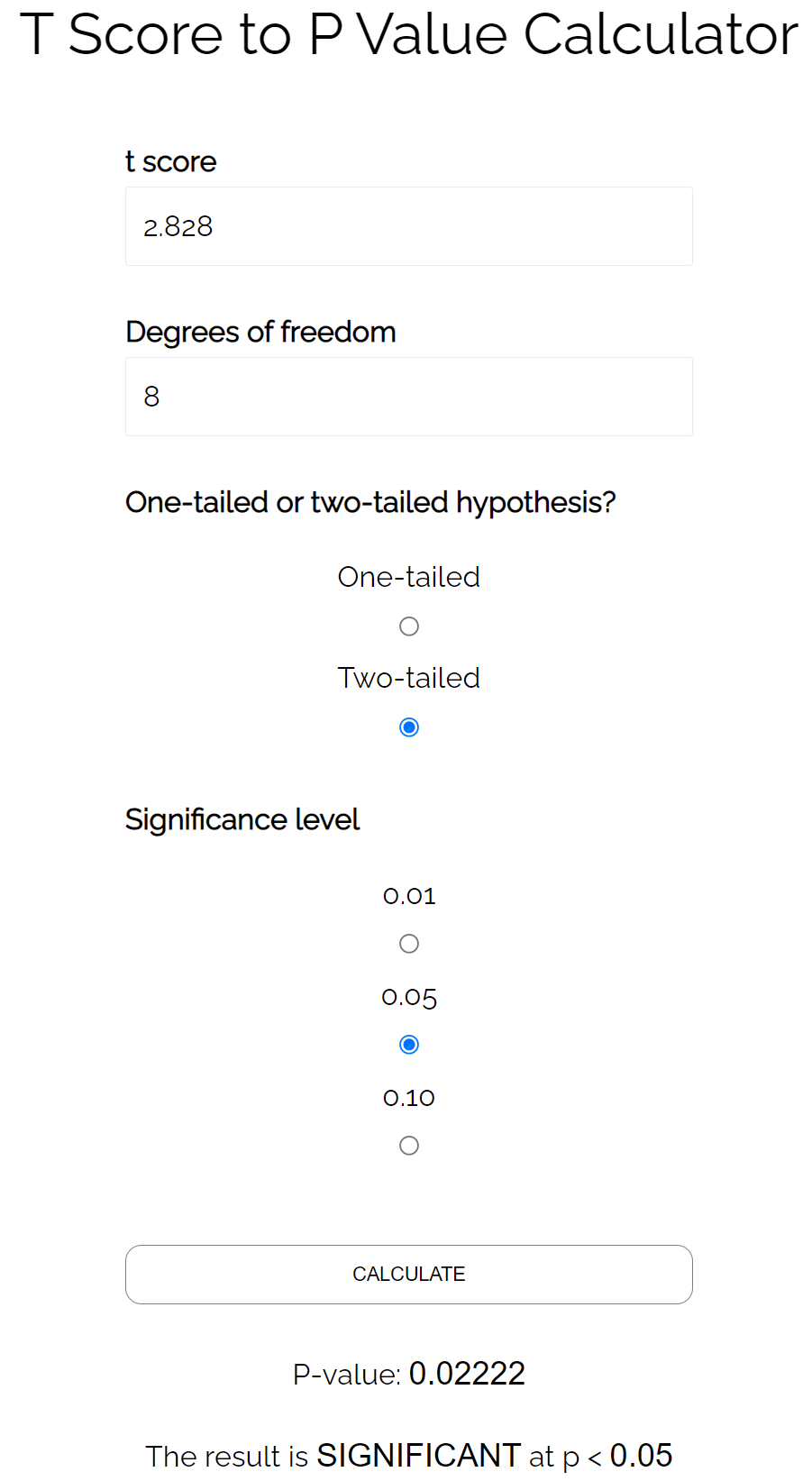
由于该 p 值小于 0.05,我们可以得出结论,这两个变量之间的相关性具有统计显着性。