如何在 r 中执行 wilcoxon 签名秩检验
Wilcoxon符号秩检验是配对 t 检验的非参数版本。当两个样本之间的差异分布不能视为正态分布时,用于检验两个总体的均值是否存在显着差异。
本教程介绍如何在 R 中执行 Wilcoxon 符号秩检验。
示例:R 中的 Wilcoxon 签名秩检验
假设一位篮球教练想知道某个训练计划是否会增加球员的罚球次数。为了验证这一点,他要求 15 名球员在训练前后各罚 20 球。
由于每个球员都可以与自己“配对”,教练计划使用配对t检验来确定训练计划前后的平均罚球次数是否存在显着差异。训练。然而,差异的分布结果是非正态的,这就是训练者使用 Wilcoxon Signed-Rank 测试代替的原因。
下表列出了训练计划前后 15 名球员每人的罚球次数(20 次尝试):
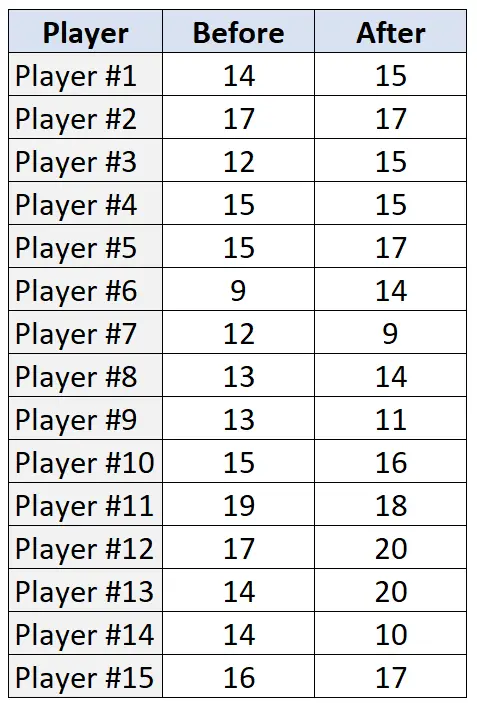
要在 R 中对此数据执行 Wilcoxon 符号秩检验,我们可以使用wilcox.test()函数,该函数使用以下语法:
wilcox.test(x, y, 偶数 = TRUE)
金子:
- x, y:数据值的两个向量
- paired:将其设置为TRUE告诉 R 我们的两个向量包含配对数据
以下代码演示了如何使用此函数对此数据执行 Wilcoxon Signed-Rank 检验:
#create the two vectors of data before <- c(14, 17, 12, 15, 15, 9, 12, 13, 13, 15, 19, 17, 14, 14, 16) after <- c(15, 17, 15, 15, 17, 14, 9, 14, 11, 16, 18, 20, 20, 10, 17) #perform Wilcoxon Signed-Rank Test wilcox.test(before, after, paired=TRUE) Wilcoxon signed rank test with continuity correction data: before and after V = 29.5, p-value = 0.275 alternative hypothesis: true location shift is not equal to 0
检验统计量为29.5 ,相应的 p 值为0.275 。由于该 p 值不小于 0.05,因此我们无法拒绝原假设。球员参加训练计划前后的罚球次数没有统计学上的显着差异。
默认情况下,此函数执行双边 Wilcoxon 符号秩检验,但您可以使用替代参数指定左手检验或右手检验:
#perform left-tailed Wilcoxon Signed-Rank Test wilcox.test(before, after, paired=TRUE, alternative="less") Wilcoxon signed rank test with continuity correction data: before and after V = 29.5, p-value = 0.1375 alternative hypothesis: true location shift is less than 0 #perform right-tailed Wilcoxon Signed-Rank Test wilcox.test(before, after, paired=TRUE, alternative="greater") Wilcoxon signed rank test with continuity correction data: before and after V = 29.5, p-value = 0.8774 alternative hypothesis: true location shift is greater than 0