如何进行 wilcoxon 符号秩检验
Wilcoxon 符号秩检验是配对 t 检验的非参数版本。它用于检验两个总体平均值之间是否存在显着差异。
何时使用 Wilcoxon 签名秩检验
当您想要使用配对 t 检验但配对之间的差异分布严重非正态分布时,请使用 Wilcoxon 符号秩检验。
确定差异是否不呈正态分布的最简单方法是创建差异的直方图,并查看它们是否遵循某种正态的“钟形”分布。
请记住,配对 t 检验对于正态分布的偏差非常稳健,因此与正态分布的偏差必须足够大才能证明使用 Wilcoxon 符号秩检验的合理性。
如何参加 Wilcoxon 签名等级测试
以下示例说明如何执行 Wilcoxon 符号秩检验。
篮球教练想知道特定的训练计划是否会增加球员的罚球次数。为了测试这一点,他要求 15 名球员在训练前后各罚 20 球。
由于每个球员都可以与自己“配对”,因此教练计划使用配对t检验来确定训练计划前后的平均罚球次数是否存在显着差异。训练。
然而,差异的分布结果是非正态的,这就是教练使用 Wilcoxon 签名等级测试来代替的原因。
下表列出了训练计划前后 15 名球员每人的罚球次数(20 次尝试):
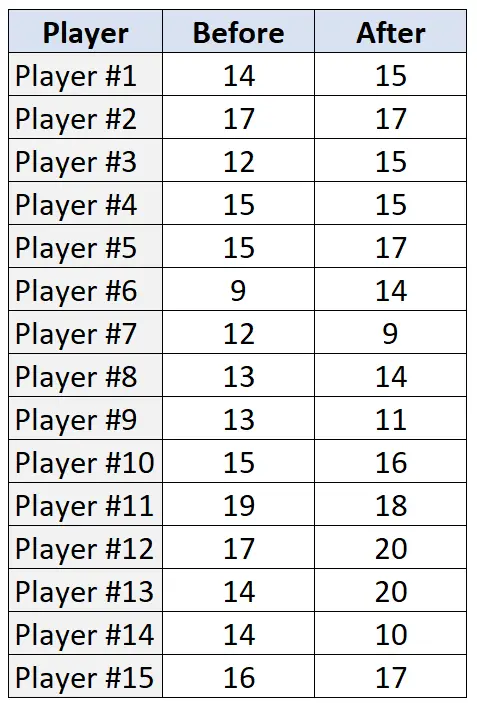
步骤 1:陈述原假设和备择假设。
H 0 :两组之间的中位数差异为零。
H A :中位数差异为负。 (例如,球员在参加训练计划之前罚球次数较少)
步骤 2:找出每对的差异和绝对差异。
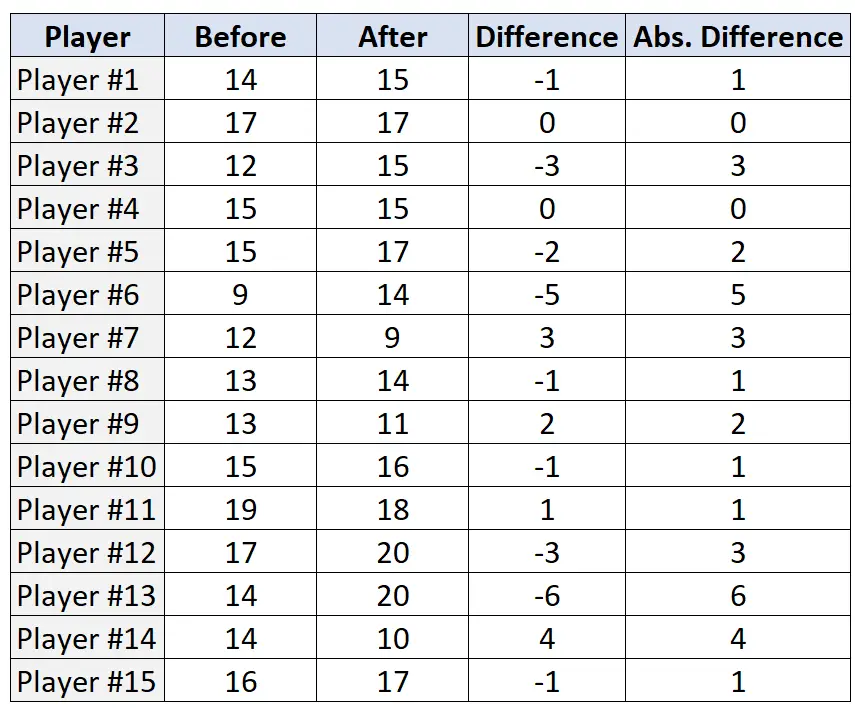
步骤 3:根据绝对差异对这些对进行排名,并按绝对差异从小到大的顺序分配排名。忽略绝对差为“0”的对,并在平局的情况下分配平均排名。
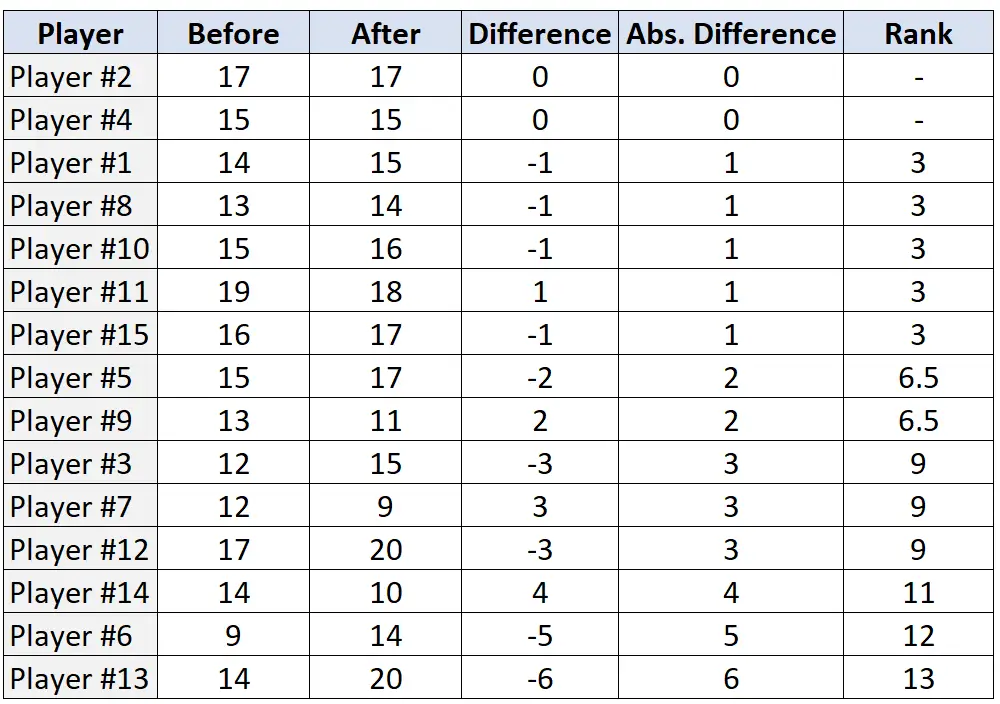
步骤 4:求正排名和负排名之和。
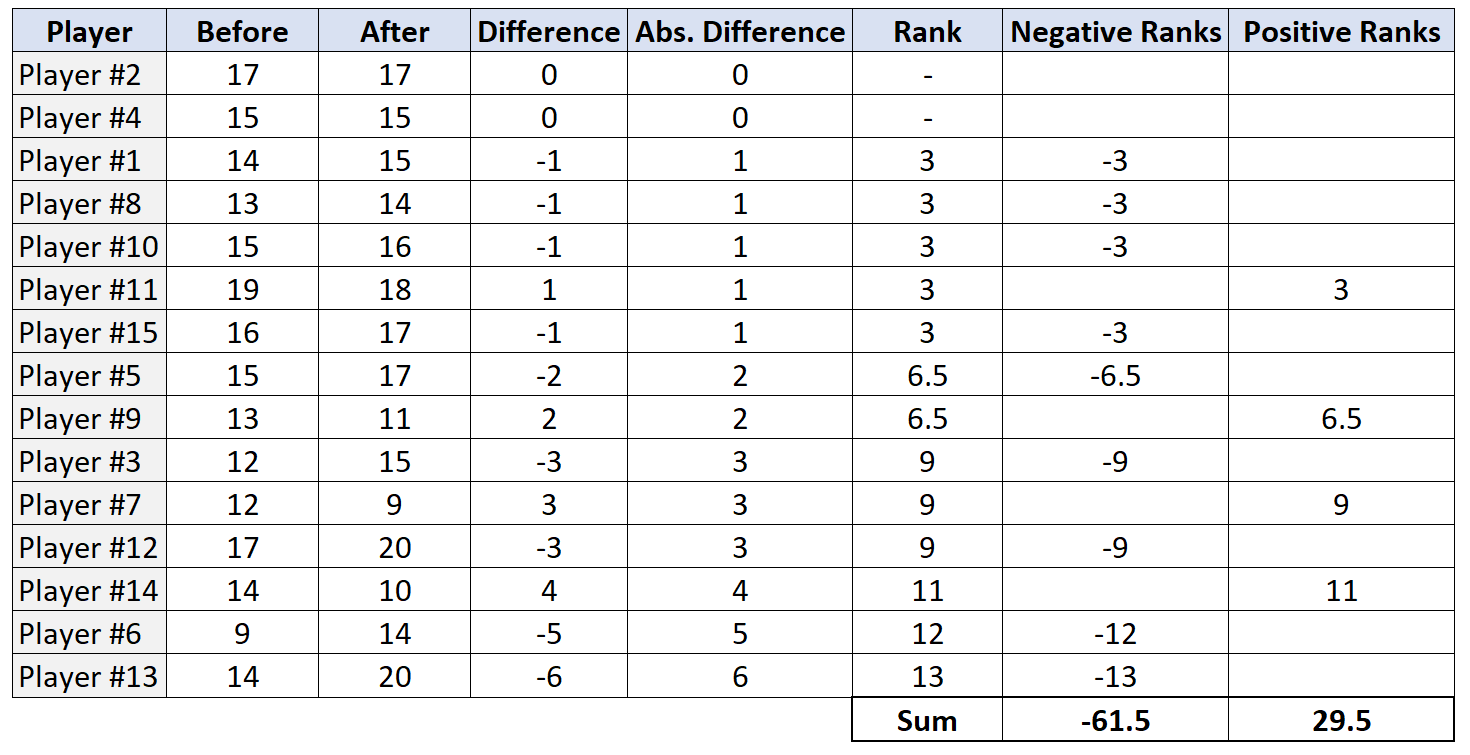
步骤 5:拒绝或不拒绝原假设。
检验统计量W是正排名和负排名的绝对值中最小的。在本例中,最小值为 29.5。所以我们的检验统计量是 W = 29.5 。
为了确定是否应该拒绝零假设,我们可以参考Wilcoxon 符号秩检验临界值表中找到的临界值,该表对应于n和所选的 alpha 水平。
如果我们的检验统计量 W小于或等于表中的临界值,我们可以拒绝原假设。否则,我们将无法拒绝原假设。
对应于 alpha 水平 0.05 和 n = 13(对的总数减去我们没有计算排名的两个对,因为它们的观察到的差异为 0)的临界值为17 。
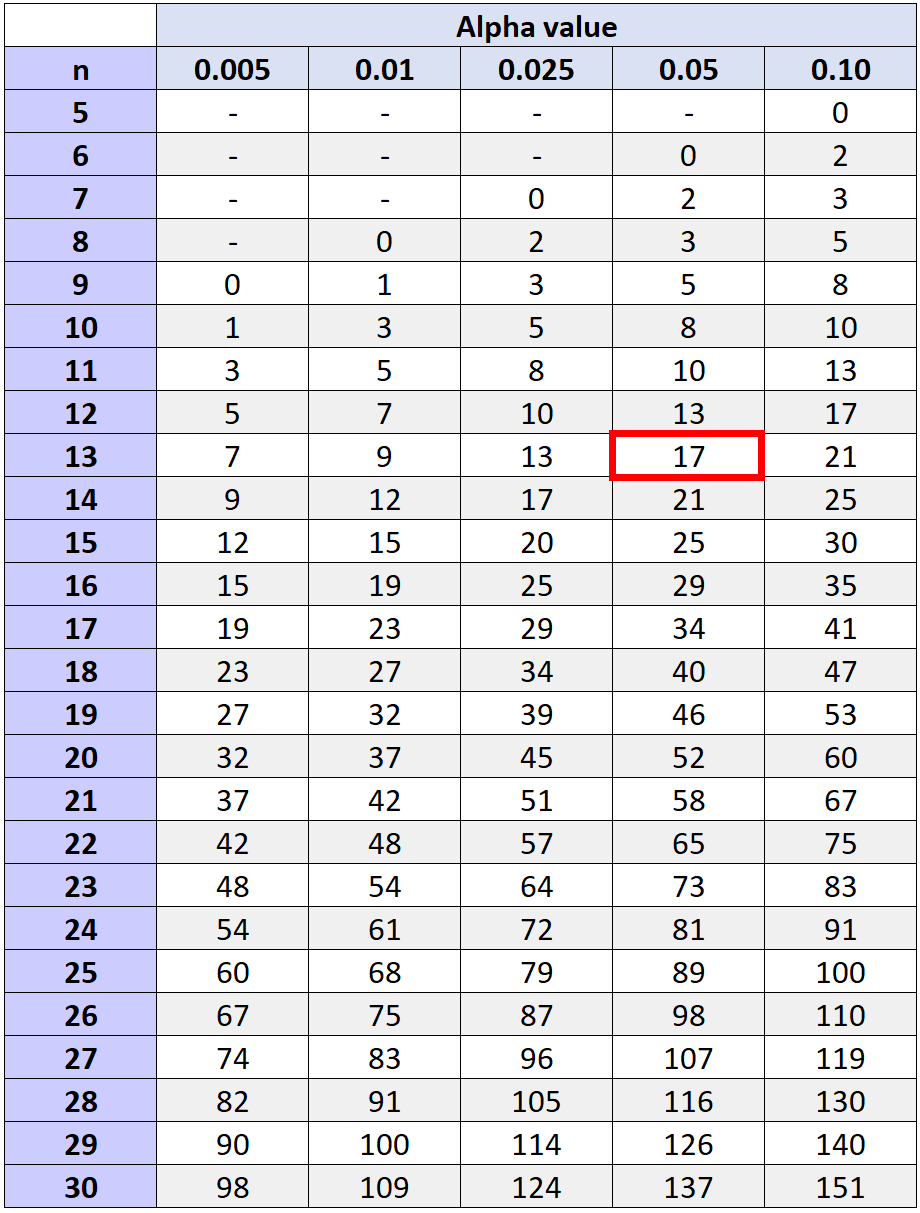
由于我们的检验统计量 (W = 29.5) 不小于或等于 17,因此我们无法拒绝原假设。我们没有足够的证据表明训练计划导致球员罚球次数显着增加。
注意:如果您想使用计算器而不是手动执行测试,请使用Wilcoxon 签名等级测试计算器。