如何在 sas 中计算 z 分数

在统计学中， z 分数告诉我们某个值与平均值的标准差有多少。

我们使用以下公式来计算 z 分数：

z = (X – μ) / σ

金子：

• X 是单个原始数据值
• μ 是数据集的平均值
• σ 是数据集的标准差

以下示例展示了如何在 SAS 中计算原始数据值的 z 分数。

示例：在 SAS 中计算 Z 分数

假设我们在 SAS 中创建以下数据集：

 /*create dataset*/
data original_data;
    input values;
    datalines ;
7
12
14
12
16
18
6
7
14
17
19
22
24
13
17
12
;
run ;

/*view dataset*/
proc print data = original_data;

现在假设我们要计算数据集中每个值的 z 分数。

我们可以使用proc sql来做到这一点：

 /*create new variable that shows z-scores for each raw data value*/
proc sql ;
    select values, (values - mean(values)) / std(values) as z_scores
    from original_data;
quit ; 

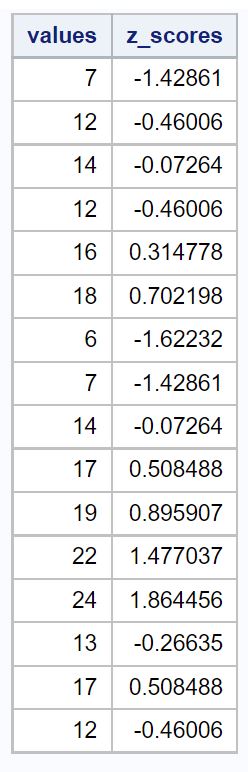
值列显示原始数据值， z_scores列显示每个值的 z 分数。

如何解释 SAS 中的 Z 分数

z 分数告诉我们某个值与平均值的标准差有多少。

z 分数可以是正数、负数或零。

正 z 分数表示特定值高于平均值，负 z 分数表示特定值低于平均值，z 分数为零表示特定值等于平均值。

如果我们计算数据集的平均值和标准差，我们会发现平均值为14.375 ，标准差为5.162 。

因此，我们数据集中的第一个值为 7，其 z 分数为 (7-14.375) / 5.162 = -1.428 。这意味着值“7”比平均值低1.428 个标准差。

我们数据中的下一个值 12 的 z 得分为 (12-14.375) / 5.162 = -0.46 。这意味着值“12”比平均值低0.46 个标准差。

值离平均值越远，该值的 z 分数绝对值就越高。

例如，值 7 比值 12 距离平均值 (14.375) 更远，这解释了为什么 7 的 z 分数的绝对值更大。

其他资源

以下文章介绍了如何在 SAS 中执行其他常见任务：

如何识别 SAS 中的异常值
如何在 SAS 中计算百分位数
如何在SAS中计算均值、中位数和众数