统计中z值和p值的差异

学生在统计学中经常混淆的两个术语是z值和p值。

要理解这些术语之间的区别，有助于理解z 检验。

z 检验有两种常见类型：

• 单样本 z 检验：用于检验总体平均值是否等于某个值。
• 双样本 z 检验：用于检验两个总体平均值是否相等。

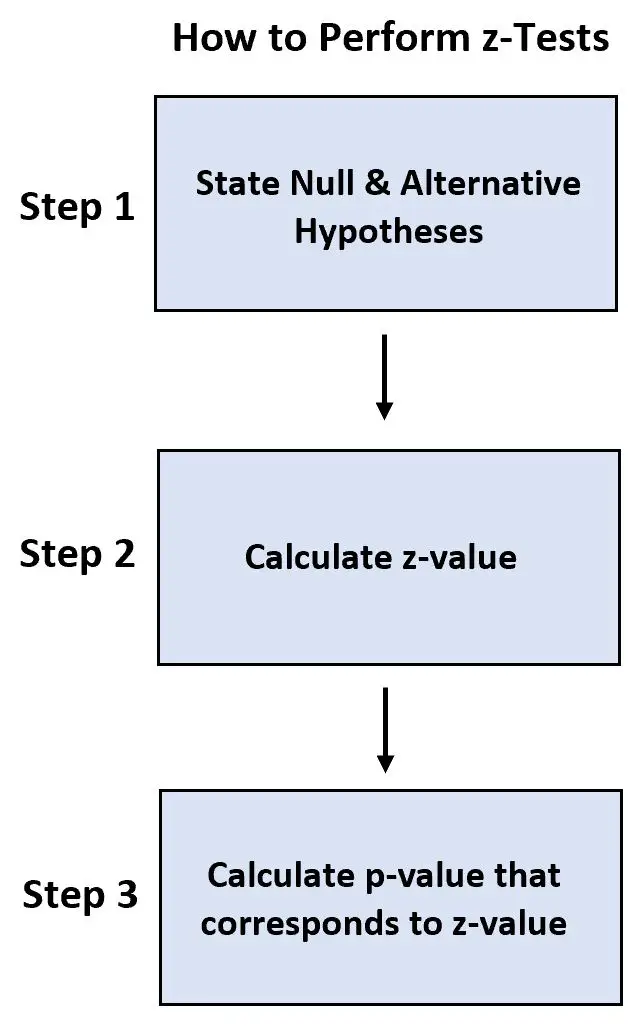
我们使用以下步骤来执行每个测试：

• 步骤 1：陈述原假设和备择假设。
• 步骤2：计算z值。
• 步骤 3：计算与 z 值对应的 p 值。

对于每个测试， z 值是量化总体均值之间差异的一种方法， p 值是获得绝对值至少与我们在“样本”中实际观察到的值一样大的 z 值的概率。数据（如果原假设确实为真）。

如果 p 值小于某个值（例如 0.05），则我们拒绝检验的原假设。

对于每种类型的 z 检验，我们对p 值感兴趣，并且只需使用z 值作为计算 p 值的中间步骤。

以下示例演示如何计算和解释两个样本 z 检验的 z 值和相应的 p 值。

示例：计算和解释 Z 值和 P 值

假设来自两个不同城市的个体的智商水平呈正态分布，每个人的总体标准差均为 15。

一位科学家想知道 A 城市和 B 城市个体的平均智商水平是否不同。因此，她从每个城市随机抽取 20 个人作为样本，并记录他们的智商水平：

A市: 82, 84, 85, 89, 91, 91, 92, 94, 99, 99, 105, 109, 109, 109, 110, 112, 112, 113, 114, 114

B市: 90, 91, 91, 91, 95, 95, 99, 99, 108, 109, 109, 114, 115, 116, 117, 117, 128, 129, 130, 133

以下是如何使用此数据执行两个样本 z 检验：

步骤 1：陈述原假设和备择假设。

首先，我们将陈述原假设和备择假设：

• H ₀ : μ ₁ = μ ₂ （两个总体平均值相等）
• H ₁ : μ ₁ ≠ μ ₂ （两个总体平均值不相等）

步骤2：计算z值。

接下来，我们将使用此数据在 Excel 中执行两个样本 z 检验，发现 z 值为-1.71817 。

步骤 3：计算 p 值。

我们可以使用Z分数到P值计算器发现-1.71817的z值对应的p值为0.08577。

由于该 p 值不小于 0.05，因此我们没有足够的证据来拒绝原假设。

因此，我们得出结论，两个城市的平均智商水平没有显着差异。

请注意，我们只是使用 z 值作为计算 p 值的中间步骤。

p 值是我们感兴趣的真实值，但我们必须首先计算 z 值。

其他资源

以下教程解释了如何使用各种统计软件执行 z 检验：

如何在 Excel 中执行 Z 检验
如何在 R 中执行 Z 测试
如何在 Python 中执行 Z 测试