如何在 ti-84 计算器上计算 z 分数
z 分数告诉我们给定值与平均值的标准差有多少。给定值的 z 分数计算如下:
z 分数= (x – μ) / σ
金子:
- x:个体值
- μ:总体平均值
- σ:总体标准差
本教程介绍如何在 TI-84 计算器上计算 z 分数。
如何计算单个值的Z分数
假设分布呈正态分布,平均值为 12,标准差为 1.4,我们想要计算单个值 x = 14 的 z 分数。要在 TI-84 计算器中计算 z 分数,我们只需输入以下公式:

这告诉我们,单个值 14 的 z 分数为1.4286 。换句话说,值 14 比平均值高 1.4286 个标准差。
如何计算多个值的Z分数
相反,假设我们有一个数据值列表,并且我们想要计算列表中每个值的 z 分数。在这种情况下,我们可以执行以下步骤:
第 1 步:输入数据。
首先,我们将输入数据值。按统计,然后按编辑。在L1列中输入以下值:
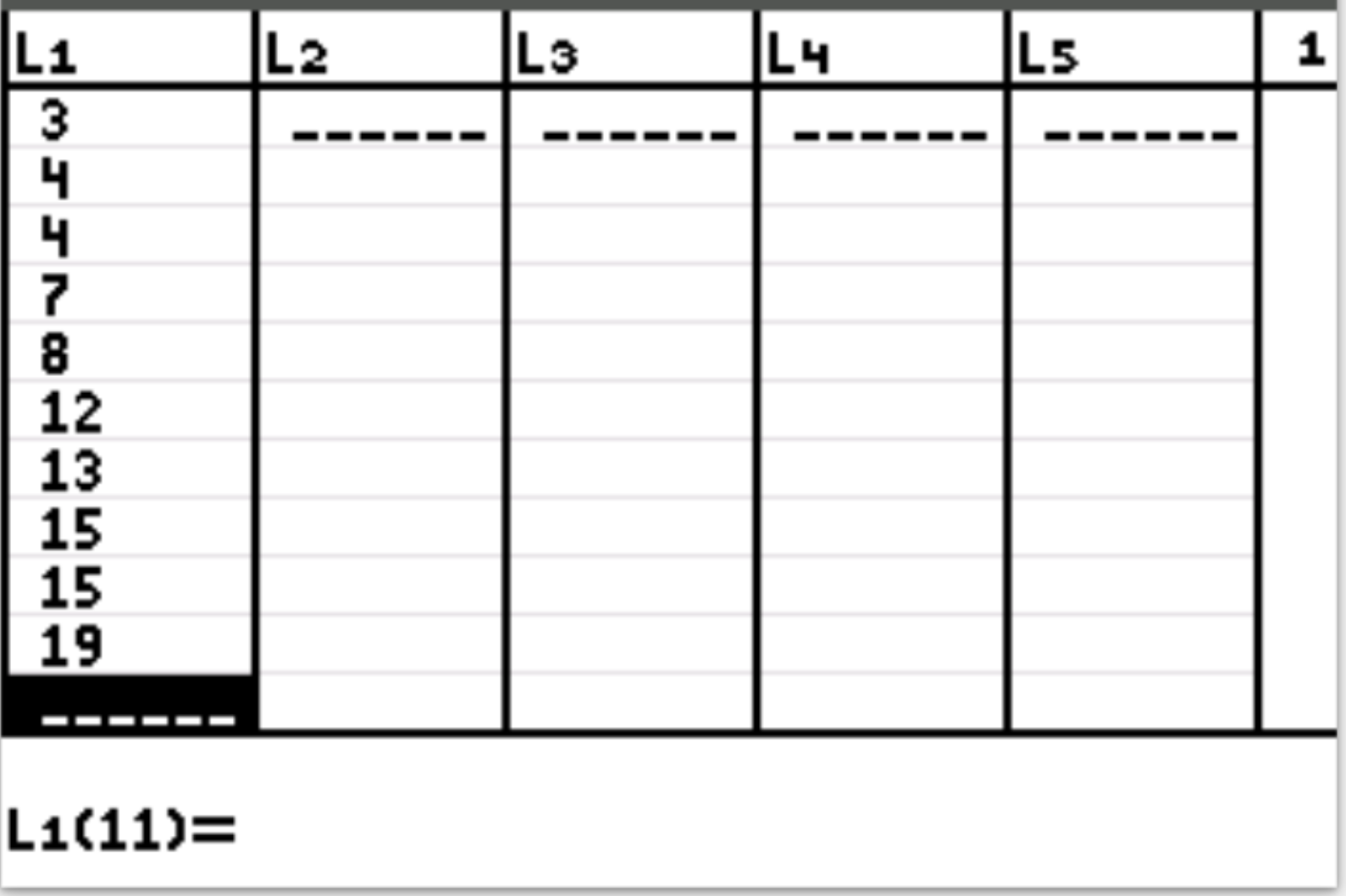
步骤 2:计算数据值的平均值和标准差。
接下来,我们将找到数据集的平均值和标准差。按Stat ,然后滚动至CALC 。突出显示Stats 1-Var并按Enter 。
对于List ,请确保选择 L1,因为这是我们输入数据的列。将FreqList留空。突出显示计算并按Enter 。

将出现以下输出:
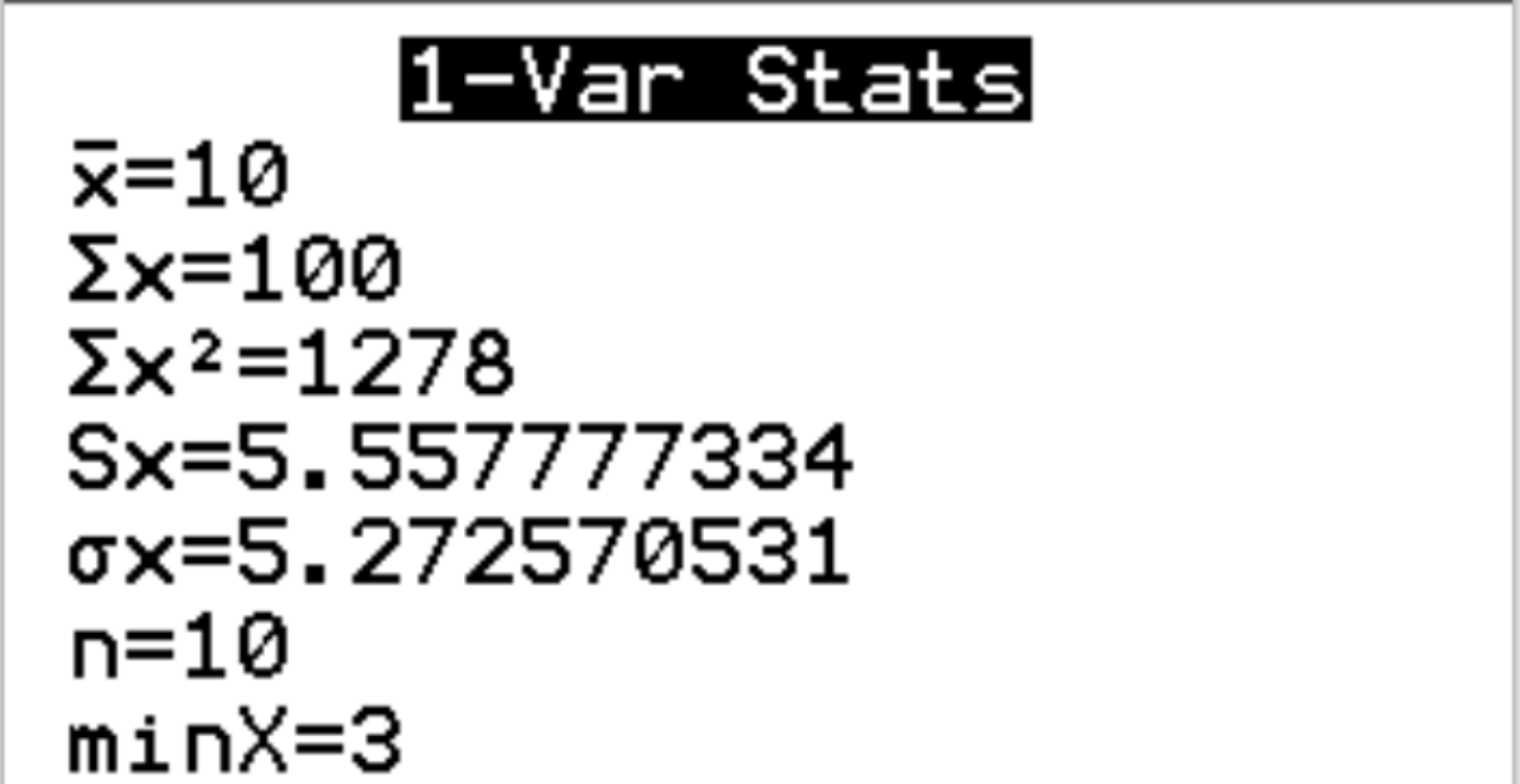
我们可以看到数据集的均值是x = 10 ,标准差是 s x = 5.558 。我们将在下一步中使用这两个值来计算 z 分数。
步骤 3:使用公式计算每个 z 分数。
接下来,我们将计算数据集中每个单独值的 z 分数。按统计,然后按编辑。突出显示 L2 并输入公式 ( L1-10)/5.558 ,然后按Enter 。每个单独值的 z 分数将自动出现在 L2 列中:
注意:要在公式中输入“L1”,请按2 ,然后按1 。
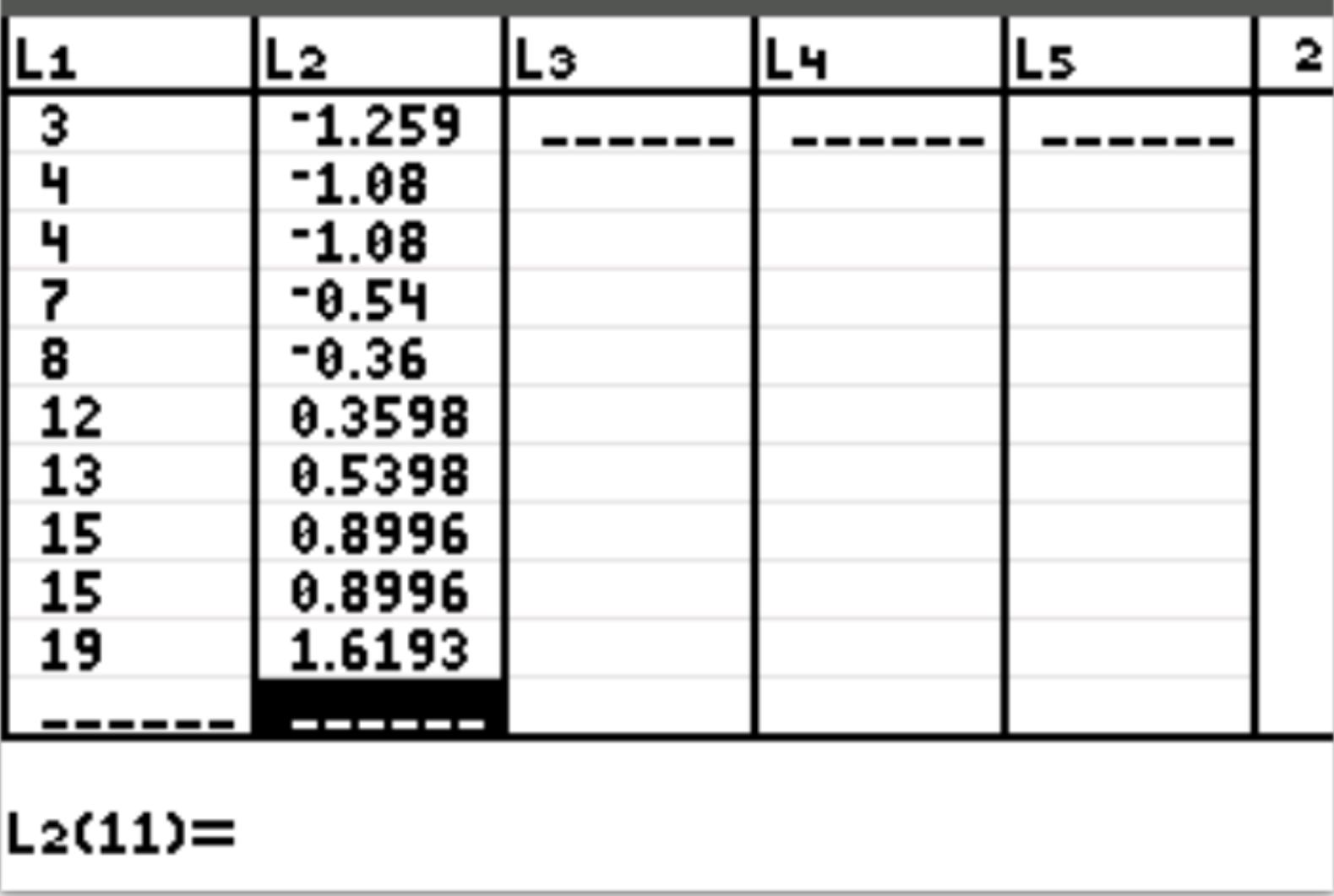
如何解释 Z 分数
请记住,z 分数只是告诉我们某个值与平均值的标准差有多少。 z 分数可以是正数、负数或等于 0:
- 正 z 分数表示特定值高于平均水平。
- 负 z 分数表示特定值低于平均水平。
- z 分数为零表示特定值等于平均值。
在我们的示例中,我们发现平均值为10 ,标准差为5.558 。
因此,我们数据集中的第一个值为 3,其 z 分数为 (3-10)/5.558 = -1.259 。这意味着值“3”比平均值低1.259 个标准差。

我们数据集中的下一个值 4 的 z 分数为 (4-10) / 5.558 = -1.08 。这意味着值“4”比平均值低1.08 个标准差。
值离平均值越远,该值的 z 分数绝对值就越高。
例如,值 3 比值 4 距离平均值更远,这解释了为什么 3 的 z 得分的绝对值更大。