什么是修改后的 z 分数？ （定义&#038；示例）

在统计学中， z 分数告诉我们某个值与平均值的标准差有多少。我们使用以下公式来计算 z 分数：

Z 分数 = ( _xi – μ) / σ

金子：

• x _i ：单个数据值
• μ：数据集的平均值
• σ：数据集的标准差

Z 分数通常用于检测数据集中的异常值。例如，z 分数小于 -3 或大于 3 的观测值通常被视为异常值。

但是，z 分数可能会受到异常大或异常小的数据值的影响。这就是为什么检测异常值的更可靠方法是使用修改后的 z 分数，计算如下：

修改后的 z 分数 = 0.6745 (x _i – x̃) / MAD

金子：

• x _i ：单个数据值
• x̃：数据集的中位数
• MAD：数据集的中值绝对偏差

修改后的 z 分数更加稳健，因为它使用中位数来计算 z 分数，而不是平均值，众所周知，平均值会受到异常值的影响。

Iglewicz 和 Hoaglin建议将修改后的 z 分数小于 -3.5 或大于 3.5 的值标记为潜在异常值。

以下分步示例展示了如何计算给定数据集的修改后的 z 分数。

第 1 步：创建数据

假设我们有以下包含 16 个值的数据集：

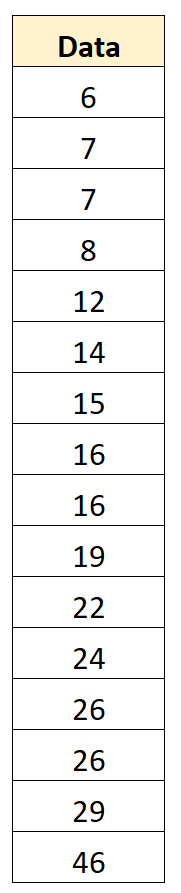
第 2 步：找到中位数

接下来，我们将找到中位数。这代表数据集的中点，结果是16 。

步骤 3：求每个值与中位数之间的绝对差

接下来，我们将求每个单独数据值与中位数之间的绝对差。例如，第一个数据值与中位数之间的绝对差计算如下：

绝对差 = |6 – 16| = 10

我们可以使用相同的公式来计算每个单独数据值与中位数之间的绝对差：

第 4 步：找到绝对中位数偏差

接下来，我们将找到绝对中位数偏差。这是第二列的中位数，结果是8 。

步骤 5：找到每个数据值的修改后的 Z 分数

最后，我们可以使用以下公式计算每个数据值的修改后的 z 分数：

修改后的 z 分数 = 0.6745 (x _i – x̃) / MAD

例如，第一个数据值的修改后的 z 分数计算如下：

修改后的 z 分数 = 0.6745*(6-16) / 8 = -0.843

我们可以对数据集中的每个值重复这个公式：

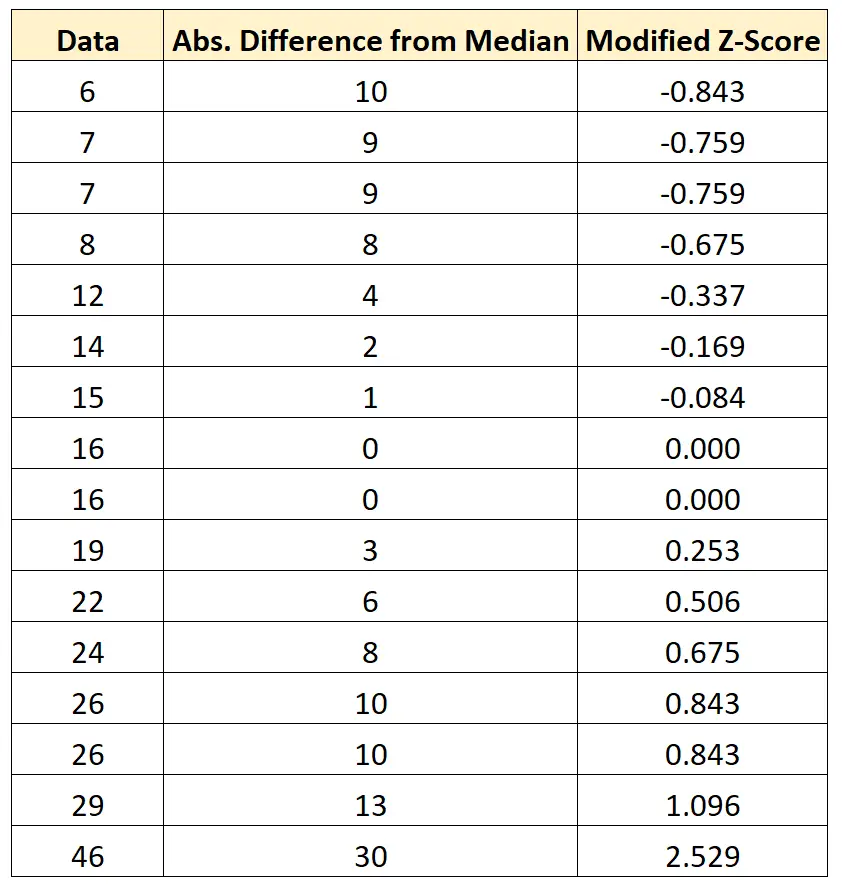
我们可以看到数据集中没有值的修改后 z 分数小于 -3.5 或大于 3.5，因此我们不会将此数据集中的任何值标记为潜在的异常值。

如何处理异常值

如果您的数据集中存在异常值，您有多种选择：

• 确保异常值不是数据输入错误的结果。有时，个人在保存数据时只是输入了错误的数据值。如果存在异常值，请首先验证输入的值是否正确并且没有错误。
• 为异常值指定一个新值。如果异常值是数据输入错误的结果，您可以决定为其分配一个新值，例如数据集的平均值或中位数。
• 删除异常值。如果该值确实是异常值，并且会对您的整体分析产生重大影响，则您可以选择将其删除。请务必在最终报告或分析中提及您删除了异常值。