Z 分数可以为负数吗？
在统计学中， z 分数告诉我们某个值与平均值的标准差有多少。我们使用以下公式来计算 z 分数：
z = (X – μ) / σ
其中 X 是我们正在分析的值，μ 是平均值，σ 是标准差。
z 分数可以是正数、负数或零。
正 z 分数表示特定值高于平均值，负 z 分数表示特定值低于平均值，z 分数为零表示特定值等于平均值。
几个例子应该可以清楚地说明这一点。
示例：计算 Z 分数
假设我们有以下数据集，显示某组植物的高度（以英寸为单位）：
5, 7, 7, 8, 9, 10, 13, 17, 17, 18, 19, 19, 20
该数据集的样本平均值为13 ，样本标准差为5.51 。
1. 在此数据集中查找值“8”的 z 分数。
以下是计算 z 分数的方法：
z = (X – μ) / σ = (8 – 13) / 5.51 = -0.91
这意味着值“8”比平均值低0.91 个标准差。
2. 在此数据集中查找值“13”的 z 分数。
以下是计算 z 分数的方法：
z = (X – μ) / σ = (13 – 13) / 5.46 = 0
这意味着值“13”恰好等于平均值。
3. 在此数据集中查找值“20”的 z 分数。
以下是计算 z 分数的方法：
z = (X – μ) / σ = (20 – 13) / 5.46 = 1.28
这意味着值“20”比平均值高1.28 个标准差。
如何解释 Z 分数
AZ 图表告诉我们有多少百分比的值低于某些 Z 分数。几个例子应该可以清楚地说明这一点。
示例 1：负 Z 分数
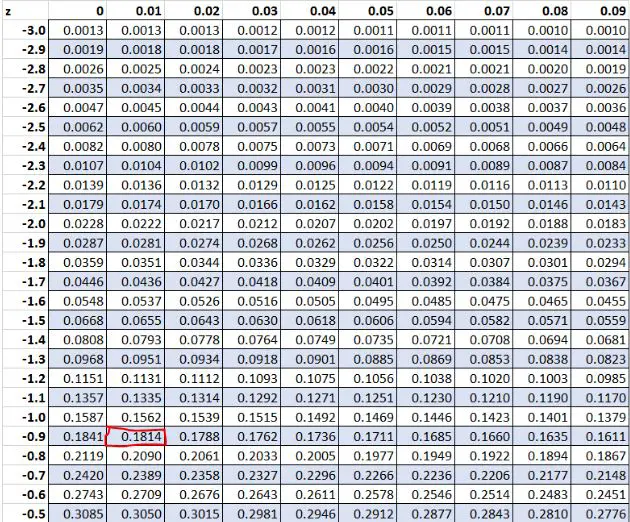
早些时候，我们发现数据集中的原始值“8”的 z 分数为-0.91 。根据Z表，有18.14%的值低于这个值。
示例 2：Z 分数等于 0
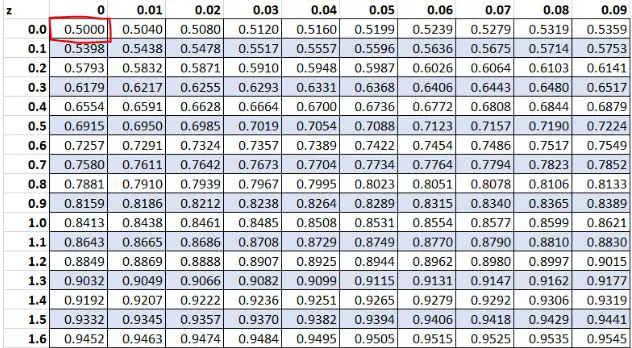
早些时候，我们发现数据集中的原始值“13”的 z 分数为0 。根据Z表，有50.00%的值小于这个值。
示例 3：正 Z 分数
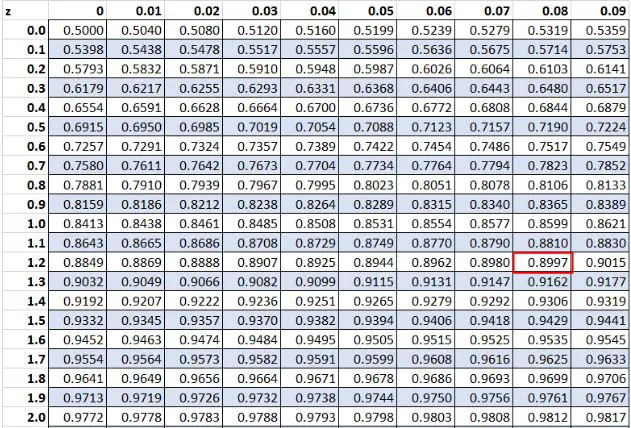
早些时候，我们发现数据集中的原始值“20”的 z 分数为1.28 。根据Z表，89.97%的值低于这个值。
结论
Z 分数可以取负无穷大和正无穷大之间的任何值，但大多数 z 分数在平均值的 2 个标准差以内。实际上，统计学中有一条称为经验法则的规则，它指出对于具有正态分布的给定数据集：
- 68%的数据值在平均值的一个标准差之内。
- 95%的数据值在平均值的两个标准差之内。
- 99.7%的数据值落在平均值的三个标准差范围内。
z 分数的绝对值越高，原始值距数据集平均值越远。 z 分数的绝对值越低，原始值越接近数据集的平均值。
相关话题：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多