Z 分数标准化：定义和示例

Z-score归一化是指对数据集中的每个值进行归一化的过程，使得所有值的平均值为0，标准差为1。

我们使用以下公式对数据集中的每个值执行 z 分数标准化：

新值 = (x – μ) / σ

金子：

• x ：原始值
• μ ：数据的平均值
• σ ：数据的标准偏差

以下示例展示了如何在实践中对数据集执行 z 分数标准化。

示例：执行 Z 分数标准化

假设我们有以下数据集：

使用计算器，我们可以看到数据集的平均值为21.2 ，标准差为29.8 。

要对数据集中的第一个值执行 z 分数标准化，我们可以使用以下公式：

• 新值 = (x – μ) / σ
• 新值 = (3 – 21.2) / 29.8
• 新值 = -0.61

我们可以使用此公式对数据集中的每个值执行 z 分数标准化：

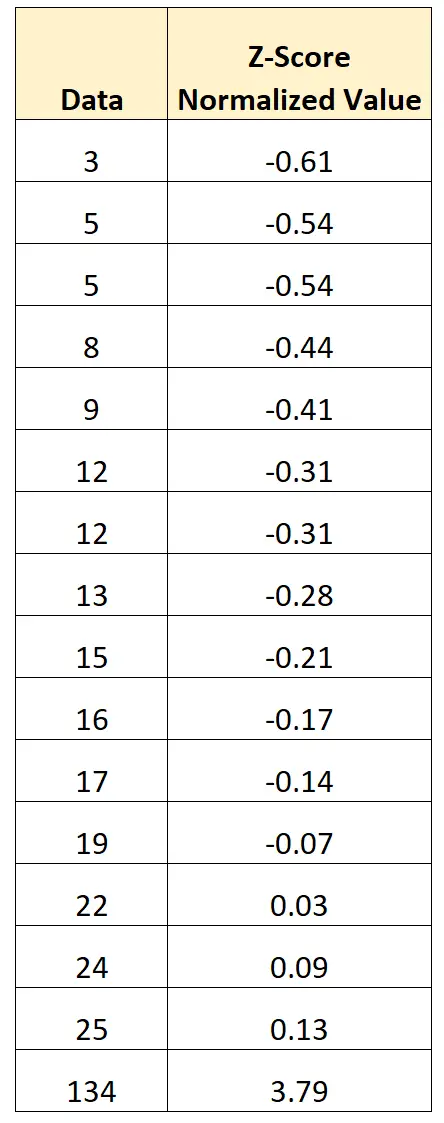
归一化值的平均值为0 ，归一化值的标准差为1 。

归一化值表示原始值与平均值之间的标准差的数量。

例如：

• 数据集中的第一个值比平均值低0.61 个标准差。
• 数据集中的第二个值比平均值低0.54 个标准差。
• ……
• 数据集中的最后一个值比平均值高3.79 个标准差。

执行这种类型的标准化的优点在于，数据集中的明显异常值（134）已被转换为不再是大量异常值。

如果我们随后使用该数据集来拟合某种类型的机器学习模型，则异常值将不再对模型拟合产生尽可能大的影响。

其他资源

以下教程提供了有关不同标准化技术的更多信息：

标准化或规范化：有什么区别？
如何标准化 0 到 1 之间的数据
如何标准化 0 到 100 之间的数据